Bille soumise à son poids et à une force constante , concours kiné Assas 2013. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

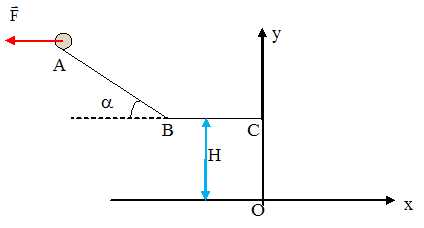
. . Une bille ponctuelle G, de masse m se déplace sur une piste rectiligne ABC. Arrivée en C, la bille chute d'une hauteur H et arrive sur le sol au point d'impact I. La portion AB de longueur L est inclinée d'un angle a avec l'horizontale. Sur tout le parcours ABCI, la bille est constamment soumise, entre autres, à une force constante F, de direction horizontale, de sens vers la gauche et de norme notée F. Les forces de frottement sont négligées dans tout l'exercice. Les expressions littérales demandées seront écrites en fonction des données adéquates de l'exercice : m, H, L, F, a et g. Portion AB. 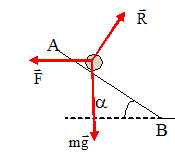Représenter sur un schéma ( sans soucis d'échelle ) et nommer extérieures appliquées à G entre A et B. La bille est soumise à la force F, à son poids ( verticale vers le bas, valeur mg ) ainsi qu'à l'action du plan ( perpendiculaire au plan ). 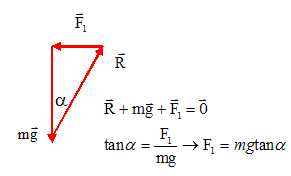Quelle est l'expression litérale de F1, la valeur de F pour laquelle G reste immobile en A ? On suppose maintenant que F < F1. La bille est lâchée sans vitesse initiale en A. . Donner, sans justification, les expressions littérales des travaux des forces appliquées à G entre A et B. L'action du plan, perpendiculaire au plan, ne travaille pas. Travail moteur du poids en descente : mg L sin a. 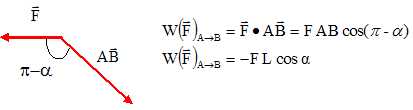Travail résistant de F : On admet que la variation de l'énergie cinétique de G entre les positions A et B est égale à la somme algébrique des travaux des forces appliquées à G entre ces deux positions. En déduire l'expression littérale de vB, la vitesse de G en B. ½mvB2 -0 = mgL sin a -FL cos a. vB2 =2L(g sin a -F/m cos a) ; vB =[2L(g sin a -F/m cos a)]½. Portion BC. Donner, sans justification, l'expression littérales des travaux des forces extérieures appliquées à G entre B et C. Le poids et l'action du plan, perpendiculaires au plan, ne travaillent pas. Travail résistant de F : - F BC. On admet que la variation de l'énergie cinétique de G entre les positions B et C est égale à la somme algébrique des travaux des forces appliquées à G entre ces deux positions. En déduire l'expression littérale de vC, la vitesse de G en C. ½mvC2 -½mvB2 = -F BC. vC2  = vB2 -2F/m BC ; vC = (vB2 -2F/m BC)½. vC = { 2L(g sin a -F/m cos a) -2F/m BC}½. Donner sans démonstration, l'expression litérale de F0, valeur de F pour laquelle G arrive en C avec une vitesse nulle. 2L(g sin a -F0/m cos a) -2F0/m BC =0. 2Lg sin a -2LF0/m cos a -2F0/m BC =0. 2F0/m ( Lcos a +BC) =2Lg sin a ; F0= mgL sin a /( Lcos a +BC). En déduire l'expression de F0 en fonction de mg si a = 60 °. cos 60 = ½ ; sin 60 = 3½/2 ;  F0= mgL 3½/2 /( 0,5L +BC). F0= mgL 3½ /( L +2BC). F0= mg 3½ /( 1 +2BC/ L).  Si BC = L alos F0 = mg 3½ /3 = mg /3½ ~ 0,58 mg. Chute de la bille entre le point C et le sol. La bille chute du point C avec une vitesse nulle. 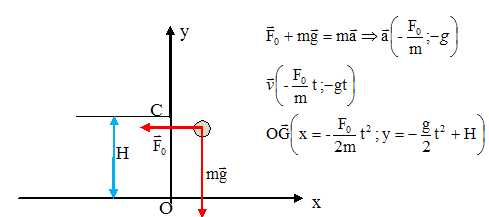Etablir dans le repère ( O, x, y), les équations horaires des coordonnées des vecteurs accélérations, vitesse et position de G en fonction de F0 et des données adéquates de l'exercice. Donner sans démonstration, l'équation de la trajectoire de G dans ces conditions, l'abscisse xI du point I. Représenter la trajectoire de G et le point d'impact I.

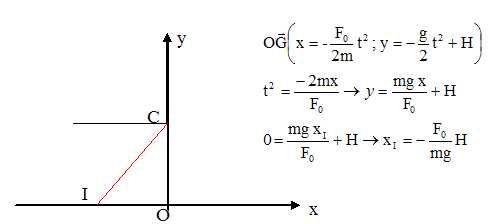
menu