|
|
|
|
Pendule
électrostatique.
On réalise un pendule électrostatique en reliant une sphère métallique
de masse m, à l'extrémité d'un fil inextensible, de masse négligeable
et de longueur L. l'extrémité supérieure du fil est fixée en un point
P. La sphère métallique, de petite dimension sera considérée comme
ponctuelle et portant la charge q.
On place la shère métallique entre les armatures verticales A et B d'un
condensateur plan non chargé.
la distace des armatures est AB = d. La sphère métallique se trouve
alors en O, situé à égales distances des armatures A et B. On applique
une tension UAB entre les armatures A et B. Il
règne un champ électrostatique entre les armatures.
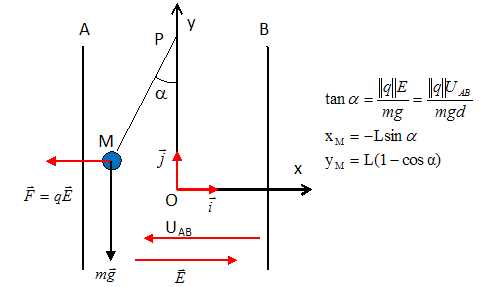
Le pendule prend une position d'équilibre, en s'écartant de
la verticale d'un angle a
et la sphère se situe en M.
Données : la direction du champ électrostatique est perpendiculaire aux
armatures et le sens de ce champ va de l'armature positive vers
l'armature négative. La valeur du champ est E = |UAB|
/ d.
UAB = 1,0 kV ; q = -15 µC ; L = 25 cm ; d = 12
cm ; m = 27 g ; g = 9,81 m s-2.
Déterminer
les coordonnées xM, yM du
point M ( en cm ). (-10,7 ; 2,4 ) ; (-10,7 ; 3,8 ) ; (0, 0
) ; (10,7 ; 2,4 ) ; (10,7 ; 3,8 ) ; aucune
réponse exacte ).
tan a =
15 10-6 *1000 /(0,027*9,81*0,12)
=0,472 ; a
=25,26°.
xM =-25 sin 25,26 = -10,7
cm ; yM = 25(1-cos25,26) =2,4 cm.
Remarque : d = 12 cm, l'abscisse -10,7 cm ne peut pas être atteinte.
|
.
|
Onde
sur une corde.
La lame métallique d'un vibreur, fixé à l'extrémité O d'une corde
tendue horizontalement, génère une onde progressive sinusoïdale de
fréquence f. L'onde se propage le long de la corde avec une célérité v.
A l'autre extrémité de la corde, on a installé un dispositif
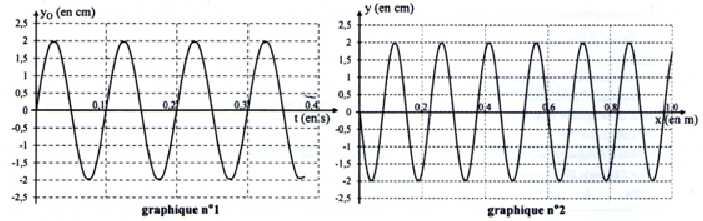
anti-réflexion. Le graphique 1 donne les variations de l'ordonnée du
point O en fonction du temps et le graphe 2 représente l'aspect de la
corde à un instant t1. L'origine des abscisses
correspond au point O.
Parmi les
affirmations suivantes, combien y en-a-t-il d'exactes ?
- La fréquence de l'onde est f = 100 Hz. Faux. Graphe 1 : période T = 0,1 s ; f
= 1T = 1/0,1 = 10 Hz.
-
La longueur d'onde est égale à l
= 20 cm. Faux. Graphe 2, 4 l = 0,6 m ; l = 15 cm.
- La célérité de l'onde est v = 1,5 m/s. Vrai. v = l f =0,15*10 = 1,5 m/s.
- L'amplitude du mouvement de O est égale à 4 cm. Faux. Amplitude = 2 cm.
- L'onde est une onde mécanique,
périodique, transversale. Vrai.
|
|
On
propose ci-dessous différentes valeurs pour t1
dont certaines ne sont pas possibles.
a =50 ms ; ß =100
ms ; g =
150 ms ; d
= 200 ms ; e =250
ms.
Indiquer
parmi les valeurs ci-dessous, celles qui ne peuvent pas correspondre à
cet instant t1.
(a ; ß) ;
( a ; g ) ; ( ß ; g ) ; ( ß ; d ) ; ( a ; e ) ; aucune
réponse exacte.
yO(t)
= 2 sin (2pft)
=2 sin (20 pt)
yO en cm et t en seconde.
yO(t1) = 0 ; sin
(20 pt1)
=0 ; 20
pt1
= k p
avec k entier positif.
t1
=k
/20 = 0,05 k seconde ; k=0, t1 = 0 s = 0 ms ; k
= 1, t1 = 50 ms ;
k = 2, t1 = 100 ms ;
k = 3, t1 = 150 ms ;
k = 4, t1 = 200 ms.
k = 5, t1 = 250 ms.
Aspect de la corde aux différents instants t1 proposés : 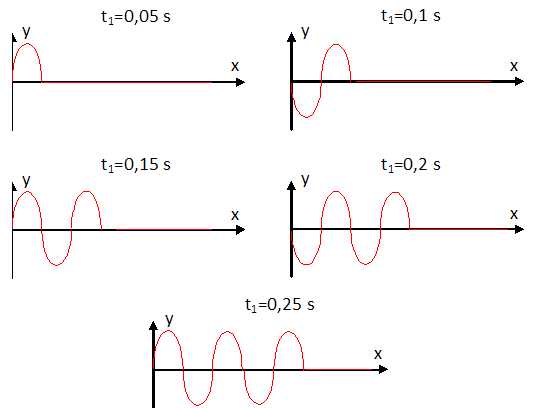
Aucun des couples proposés ne correspond au graphique 2.
|
|