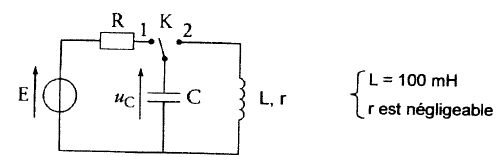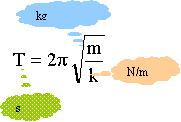|
|
|
|
A propos des
ondes.
Les ultrasons sont utilisés en médecine pour réaliser des examens
échographiques..
A) Ces ondes
sont des ondes mécaniques. Vrai.
B) Ce sont des ondes longitudinales. Vrai.
C) Elles sont de même nature que les rayons X. Faux.
Les rayons X sont des
ondes électromagnétiques.
D) Les ultrasons se propagent avec transport d'énergie sans transport
de matière. Vrai.
E) Le ultrasons ne peuvent pas être diffractés. Faux.
La diffraction est une
propriété générale de toutes les ondes.
On
considère une onde lumineuse monochromatique appartenant au domaine
visible.
A) Cette onde possède une fréquence supérieure à celle d'une onde
infrarouge. Vrai.

B)
Il s'agit d'une onde mécanique. Faux.
Il s'agit d'une onde
électromagnétique.
C) Elle est diffractée quand elle change de milieu de propagation. Faux.
Elle peut être réfractée
( réfraction) en changeant de milieu de propagation.
D) Sa longueur d'onde dépend de l'indice de réfraction du milieu dans
lequel elle se propage. Vrai.
E) Elle se propage dans le vide avec la même célérité c quelle que soit
sa longueur d'onde. Vrai.
Origine des
éléments chimiques.
La théorie du Big-Bang permet d'expliquer la formation des éléments les
plus légers, l'hydrogène et l'hélium-3, dans les trois minutes qui ont
suivi l'explosion originelle. Les noyaux les plus lourds se forment
dans les étoiles.
Masse des noyaux : m(11H) =1,00728 u ; m(42He)
= 4,0015 u ; m(01e) = 5,486 10-4 u.
1 u = 1,660 54 10-27 kg. 1eV = 1,6 10-19 J.
Dans le soleil, les noyaux d'hydrogène
réagissent par fusions nucléaires et donnent naissance à l'hélium-4
selon :
4 11H ---> 42He + 2
01e.
Calculer
en joule l'énergie libérée lors de cette fusion.
Défaut de masse Dm = m(42He)
+ 2m(01e)
-4m(11H)
= 4,0015 +1,0972 10-3
-4,02912 =-2,65228 10-2 u.
Soit : -2,65228 10-2 *1,660
54 10-27 = -4,404217 10-29 kg.
Energie libérée : Dm c2 = -4,404217 10-29
*9,0 1016 = -3,9638 10-12 ~ -4,0 10-12 J.
On
considère que l'énergie produite et rayonnée par le soleil provient
entièrement de cette fusion. Cette énergie rayonnée en une année,
supposée constante, est de 1,2 1034 J an-1. 10 %
de la masse du soleil ( M = 1,99 1030 kg) est constituée
d'hydrogène pouvant fusionner.
Au
bout de combien d'année le soleil aura-t-il consommé cette quantité
d'hydrogène ?
Masse d'hydrogène pouvant fusionner : 1,99 1029 kg.
Nombre de fusion : 1,99 1029 / (4*1,0072
*1,660 54 10-27 )
=2,97 1055.
Energie libérée : 2,97
1055*3,9638 10-12 =1,18 1044 J.
Durée : 1,18 1044 /1,2 1034 = 9,8 109 ans.
Les
éléments les plus lours se forment dans les étoiles plus massives que
le soleil. En fin de vie ces étoiles explosent en supernova. Le nickel 5628Ni
instable est ainsi formé. Il se désintègre en 5627Co
qui lui même donne naissance au fer 5626Fe
dans un état excité.
Ecrire
les équations de désintégration conduisant au fer.
5628Ni
--> 5627Co
+ 01e. 5627Co
-->5626Fe*
+ 01e.
Quel
est le rayonnement émis par le fer-56 quand il se désexcite ?
Rayonnement gamma. |
Capteur
d'humidité.
Un condensateur est chargé à travers une résistance R ( interrupteur K
en position 1).
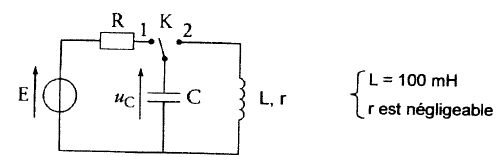
On bascule l'interrupteur K en position 2. La tension aux bornes du
condensateur varie selon l'équation : uc(t) = 4 cos (3 103
t + p/3. On prendra p = 3.
Déterminer
la période propre T0 du circuit.
3 103 = 2 p /T0
; T0 = 6 / (3 103) =2 10-3 s.
Calculer
la valeur de la capacité C.
T0 = 2p(LC)½
; LC = (T0 / (2p)2
; C = 1 /L (T0 / (2p)2 = 10 ( 2 10-3/ 6)2 =1,1 10-6 F.
Un capteur d'humidité comporte un condensateur dont la capacité
augmente de façon linéaire affine avec le taux d'humidité t. Cette variation est de 0,4 nF
par % de taux d'humidité. C = 16 nF pour t = 10 %.
Donner
l'expression de C en fonction de t.
C = a t+b ; a = 0,4 nF %-1
; b = C - a t = 16 -0,4*10 = 12 nF. C = 0,4 t +12.
Ce capteur est associé à une bobine d'inductance L et de résistance
négligeable dans le circuit précédent. La capacité C calculée en
fonction des nouvelles variations de uc(t) enregistrées est
de 24 nF.
Quel est
le taux d'humidité ?
t =(C-12) / 0,4 =
(24-12) / 0,4 = 30 %.
|
Skieur.
Un skieur de masse m = 70 kg glisse sur une piste enneigée. Il démarre
sans vitesse initiale de A situé à une hauteur h=zA =5 m.
Sur la partie ABC, la trajectoire du centre d'inertie G du skieur est
un arc de cercle de rayon R = 6 m, de centre O1. On prendra
g = 10 m s-2. Les frottements sont négligeables sur cette
partie.
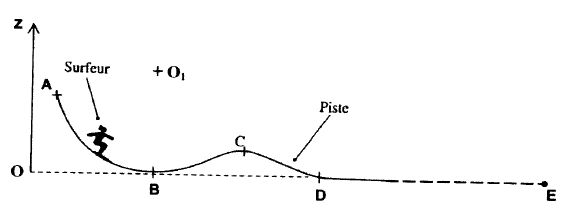
Calculer
la vitesse du skieur en B.
Entre A et B, seul le poids travaille. Ecrire le théorème de l'énergie
cinétique entre A et B :
½mvB2 -0 = mg(zA-zB) ; vB
= (2gzA)½ =(2*10*5)½ = 10 m/s.
Déterminer
la composante normale du vecteur accélération en B.
aN = vB2 / R =100 / 6 = 16,66 ~17 m s-2.
Quelle
est sa vitesse en C ( zC = 2 m) ? Représenter le
vecteur vitesse en C sans échelle précise.
Entre A et C, seul le poids travaille. Ecrire le théorème de l'énergie
cinétique entre A et C :
½mvC2 -0 = mg(zA-zC) ; vB
= (2g(zA-zC))½ =(2*10*3)½
=7,75 ~ 7,7 m/s.
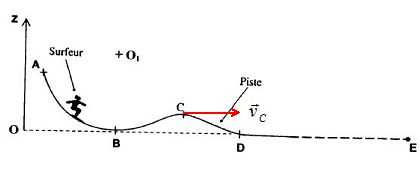
Lorsqu'il
aborde en D la partie horizontale, le skieur a une vitesse vD
= 8 m/s. L'ensemble des forces de frottements agissantsur lui est alors
assimilé à une force F horizontale. Le skieur parcourt 30 m sur le plan
horizontal et s'immobilise en E.
Déterminer
la valeur de F.
Entre D et E seule la force de frottement travaille, le poids et
l'action du plan étant perpendiculaires au déplacement.
Ecrire le théorème de l'énergie cinétique entre D et E :
0-½mvD2 = -F DE ; F = = ½mvD2
/ DE =0,5*70 *82 / 30 ~ 75 N.
|
Sismomètre.
Un
sismomètre permet de détecter et d'enregistrer de très faibles
mouvements du sol. Son fonctionnement est basé sur l'utilisation d'un
oscillateur solide-ressort. Considérons un oscillateur mécanique
horizontal susceptible d'être excité par une onde sismique
longitudinale. Il est constitué d'un ressort de masse négligeable et
d'un solide S de masse m =200 g. Une des extrémités du ressort de
constante de raideur k =10 N m-1 est fixe et l'autre est
accrochée au solide S qui se déplace sur un support rectiligne
horizontal. Le centre d'inertie G du solide est repéré par son abscisse
x(t) sur l'axe x'Ox. Il se situe au point O lorsque la longueur du
ressort est celle de sa longueur à vide. Le solide est écarté de sa
position d'équilibre et abandonné sans vitesse initiale à t = 0. On
néglige les frottements et on prend p = 3.
Ecrire l'équation différentielle du mouvement de G et en déduire une solution de cette équation.
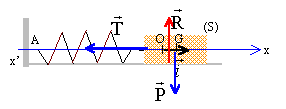
Poids et action du support se neutralisent.
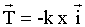 tension
du ressort tension
du ressort
La seconde loi de Newton s'écrit, le
référentiel terrestre étant
supposé galiléen :
projection sur l'axe x'x :
-k x = mx" ou x" + k/m x=0 ; pulsation w² = k/m.
Solution de cette équation : x(t) = Xmax cos (wt +f).
Les constantes Xmax et f sont déterminées par les conditions initiales.
Calculer la période propre T0 de cet oscillateur.
période : 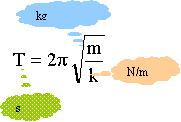
T0=2*3(0,2 / 10)½ =0,8485 ~0,85 s.
Lors d'un séisme le sismomètre fonctionne en oscillations forcées.
L'onde sismique longitudinale est assimilée à une excitation
sinusoïdale de période TS et d'amplitude AS.
Quelle est, après le régime transitoire, la période des oscillations de l'appareil soumis à une onde sismique longitudinale ?
L'excitateur force l'oscillateur à osciller à la période TS.
Quelle doite être la période de l'onde sismique pour que le sismomètre entre en résonance ?
Lorsque TS ~ T0 l'oscillateur entre en résonance.
Que
peut-on dire de l'amplitude des oscillations du sismomètre pour des
ondes sismiques de même amplitude et de fréquence inférieure à celle de
la résonance ?
A la résonance l'amplitude des oscillations du sismomètre est maximale. Pour une fréquence excitatrice inférieure à f0, l'amplitude des oscillations du sismomètre sera plus petite.
|
|