|
|
|
|
On
appelle pendule simple un système constitué d'un objet dense, de masse
m suspendu à un fil inextensible, de longueur L et de masse négligeable
devant m, accroché à une extrémité fixe. La taille de l'objet est
négligeable devant L.
On se propose d'étudier différents aspects de ce modèle physique.
A. Aperçu historique.
Extrait de "Discours et démonstrations " de Galilée ( 1564-1642).
Il s'agit d'une discussion entre Salviati ( Galilée) et Sagrédo ( un de ses élèves).
Salviati
:" Pour obtenir un premier pendule dont la durée d'oscillation soit
double de celui d'un second pendule, il convient de donner au
premier une longueur quadruple de celle du second".
Sagrédo:" si
j'ai bien compris, je pourrais donc aisément connaître la longueur
d'une corde, quand bien même son point de suspension serait invisible
et que l'on apercevrait seulement son extrémité inférieure. Si en effet
j'attache en cette partie de la corde une masse fort lourde à laquelle
je communique un mouvement de va et vient, et si un ami compte le
nombre d'oscillations pendant que moi-même je compte les oscillations
effectuées par un autre pendule suspendu à un fil mesurant
exactement une coudée, alors grâce au nombre d'oscillations de ces deux
pendules pendant une même durée je trouverai la longueur de la corde ;
supposons par exemple que mon ami ait compté 20 oscillations de la
grande corde, dans la même durée où j'en comptais 240 pour mon fil long
d'une coudée..."
L'affirmation de Salviati :" On considère qu'une oscillation correspond à un mouvement d'aller et retour du pendule."
Quelle grandeur physique est désignée par l'expression " la durée d'une oscillation" ?
La période du pendule, notée T, exprimée en seconde.
Montrer qu'une seule des propositions suivantes satisfait à l'affirmation de salviati.
La durée des oscillations est proportionnelle à : 1/L ; L½ ; L2.
"
Pour obtenir un premier pendule dont la durée d'oscillation soit double
de celui d'un second pendule, il convient de donner au premier une
longueur quadruple de celle du second".
La durée des oscillations est proportionnelle à L½.
La réponse de Sagrédo : on note respectivement L1 et T1 la longueur et la durée d'une oscillation du pendule de Sagrédo, L2 et T2 la longueur et la durée d'une oscillation du pendule d'un ami de Sagrédo.
On admet qu'une coudée équivaut à 50 cm : L1 = 50 cm.
En utilisant la réponse de Sagédo, déterminer la valeur numérique du rapport T1/T2.
"mon ami ait compté 20 oscillations de la grande corde, dans la même durée où j'en comptais 240 pour mon fil long d'une coudée".
T1 = durée / 240 ; T2 = durée / 20 ;
T1/T2 = 20 / 240 = 1 / 12.
Calculer la longueur L2.
T1 = k L1½ ; T2 = k L2½ ; k est une constante. T1/T2 = (L1/L2)½ = 1/12.
L1/L2= 1/144 ; L2 = 144 L1=144*0,50 = 72 m.
|
.
|
B. Etude expérimentale.
On
se propose d'étudier expérimentalement l'influence de différents
paramètres sur la durée d'une oscillation d'un pendule simple. Pour
cela, on utilise un filinextensible de longueur L et de masse
considérée comme nulle. Les objets denses de masse m, suspendus au fil,
sont sufisamment petits pour que leur taille soit négligeable devant L.
Le pendule ainsi constitué est écarté de sa position d'équilibre d'un angle q0
petit ( inférieur à 10 ° ) puis lâché sans vitesse initiale. On obtient
alors des oscillations libres amorties dont la durée d'une oscillation
ou pseudo-période est notée T. On mesure à l'aide d'un chronomètre la
durée Dt nécessaire pour réaliser 20 oscillations.
Influence de la masse.
On réalise une série de mesures de Dt avec un fil de longueur L = 24,4 cm et différents objets de masse m.
| m(g) | 60 | 125 | 160 | 200 | | Dt(s) | 19,9 | 19,8 | 19,9 | 19,9 |
Que peut-on déduire quand à l'influence de la masse sur la pseudo-période du pendule. Justifier.
T = Dt / 20 : T reste pratiquement constante que'elle que soit la masse m.
La pseudo-période est indépendante de la masse m.
Influence de la longueur L.
On suspend maintenant un objet de masse m = 125 g et on fait varier la longueur du fil.
| L(cm) | 12,3 | 24,4 | 28,6 | 32,4 | 38,5 | | Dt(s) | 14,1 | 19,8 | 21,4 | 22, | 24,9 |
On trace les trois graphes suivants..
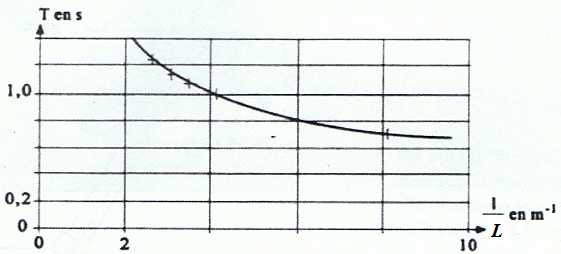
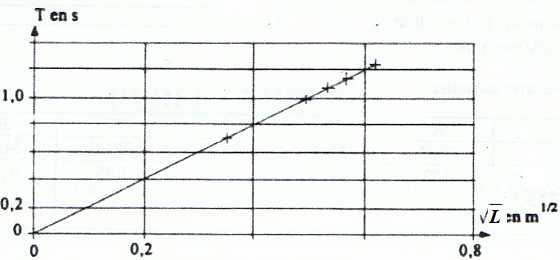
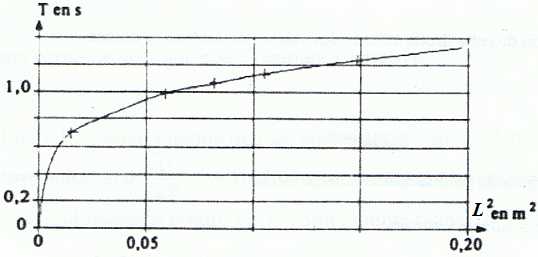
Quel est le graphique le plus simple à exploiter ?
Le graphique n°2 est une droite passant par l'origine.T et L½ sont proportionnelles. Ce graphe est le plus simple à exploiter.
La relation littérale entre T et L peut s'écrire T = k La.
Déterminer k et a.
T et L½ sont proportionnelles : a = ½.
k est égal au coefficient directeur de la droite soit : 1,2 / 0,60 = 2,0 s m-½.
k = T / L½ = 2,0 s m-½.
|
C. Influence de la valeur du champ de pesanteur.
On
ne peut pas modifier la valeur de g du champ de pesanteur. Toutefois,
grâce au dispositif ci-dessous tout se passe comme si le pendule était
vertical et placé dans un champ de pesanteur de valeur g' = g sin a.
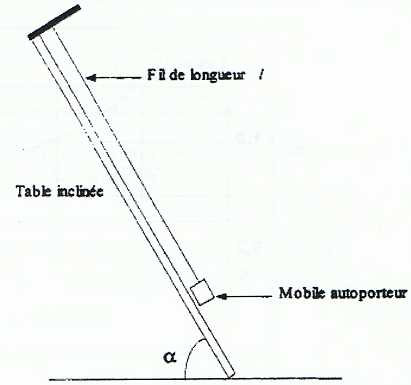
Sur une rable inclinée d'un angle a
par rapport à l'horizontale un petit mobile autoporteur de masse m =
125 g est suspendu à un pont fie,par un fil de longueur L = 24,4 cm.
Pour différentes valeurs de a, on modifie la valeur de g' et on mesure la durée Dt de 20 oscillations de faible amplitude.
| a(degré) | 90 | 70 | 50 | 30 | 20 | 10 | | Dt(s) | 19,84 | 20,46 | 22,32 | 27,90 | 34,10 | 47,74 | | 1 / g'½ | 0,32 | 0,33 | 0,36 | 0,45 | 0,55 | 0,77 | | T(s) | 19,84/20 =0,992 | 1,023 | 1,116 | 1,395 | 1,705 | 2,385 | | T g'½ (m½) | 0,992/0,32=3,1 | 3,1 | 3,1 | 3,1 | 3,1 | 3,1 |
La courbe représentant la pseudo-période T en fonction de 1 / g'½ est une droite passant par l'origine.
Donner l'équation de cette droite.
T g'½ = 3,1 soit T = 3,1 / g'½.
Conclusion.
La pseudo-période peut se mettre sous la forme T = C (L/g)½ où C est une constante.
Montrer que C est sans dimension.
C = T(g/L)½ avec T en seconde, L en mètre et g en m s-2.
Dimension de C : [C]= s m½s-1 m-½= 1 ; C est donc sans dimension.
Déterminer la valeur de C à partir de la valeur de k.
k = T / L½ = 2,0 s m-½.
T = C (L/g)½ soit T / L½ =C/g½. C = 2,0 *9,8½ =6,26 ~2p.
Déterminer la valeur de C à partir de l'équation de la droite trouvée ci-dessus.
T g'½ = 3,1 = CL½ ; C = 3,1 / 0,244½ =6,28 ~ 2 p.
Conclure en donnanr l'expression de la pseudo-période T d'un pendule.
T = 2 p (L/g)½.
|
|