Casque audio à réduction de bruit.
Bac S
2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
|
|
|
|
Il
existe aujourd’hui des casques audio qui présentent, en plus de la
réduction passive, un dispositif dit « actif » qui tend à supprimer les
bruits résiduels à l’intérieur des oreillettes.
La « réponse en fréquence » du casque est-elle adaptée à l’audition humaine ?
Réponse en fréquence du casque : 10 - 25 000 Hz.
Réponse en fréquence de l'oreille humaine : 20 - 20 000 Hz.
Ce casque est donc adapté à l'audition humaine.
Une enceinte acoustique émet un signal sonore de fréquence f et d’intensité I toutes
deux réglables.Le capteur d’un premier sonomètre est placé entre les
deux oreillettes du casque. Les oreillettes sont en outre maintenues
plaquées l’une contre l’autre de manière à enfermer le mieux possible
le capteur. Ce sonomètre mesure ainsi le niveau d’intensité sonore L
entre les oreillettes. Casque et sonomètre sont placés face à
l’enceinte.
Un deuxième sonomètre mesure le niveau d’intensité sonore à proximité immédiate du casque.
Les niveaux d’intensité sonore mesurés en fonction de la fréquence sont représentés ci-dessous :
- niveau d’intensité sonore ambiant à proximité immédiate du casque (cas n°1) ;
- niveau d’intensité sonore entre les oreillettes lorsque le dispositif
actif est éteint et que les oreillettes interviennent seules (cas n°2) ;
- niveau d’intensité sonore entre les oreillettes lorsque le dispositif actif fonctionne (cas n°3)
|
|
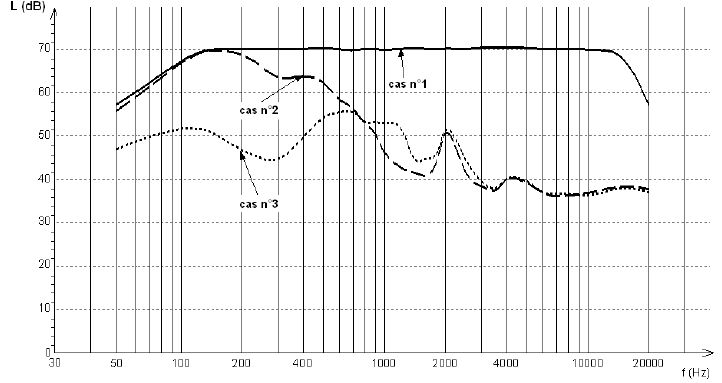
Identifier approximativement les domaines de fréquence pour lesquels :
- seules les oreillettes sont efficaces pour la réduction du bruit ambiant ;
Les oreillettes réduisent le niveau sonore de 30 dB pour les fréquences
comprises entre 1000 et 1800 Hz ainsi qu'entre 3000 et 20 000 Hz.
- seul le dispositif actif est efficace pour la réduction du bruit ambiant ;
Le dispositif actif le niveau sonore d'au moins 25 dB pour les
fréquences comprises entre 200 et 400 Hz, entre 1500 et 1800 Hz ainsi
qu'entre 3000 et 20 000 Hz.
- les deux dispositifs participent ensemble à la réduction du bruit ambiant.
Les deux dispositifs réduisent ensemble le niveau sonore d'au moins 25
dB pour des fréquences comprises entre 200 et 400 Hz, 1000 et 1800 Hz
ainsi qu'entre 3000 et 20 000 Hz.
Ces résultats sont conformes avec la notice " fonction réduction de bruit active jusqu'à 20 dB".
|
| .
. |
|
|
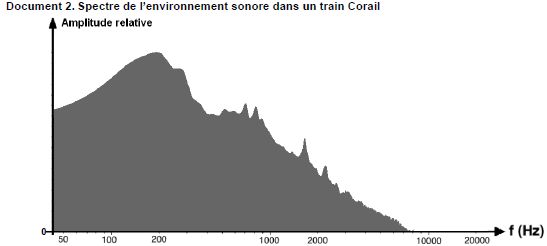
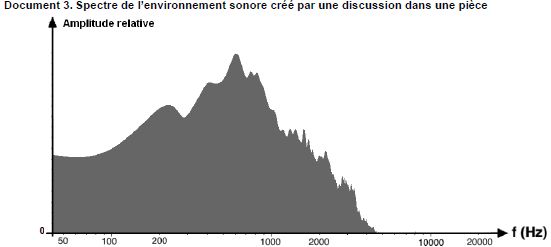
Le
casque à réduction de bruit est ensuite testé dans deux environnements
sonores différents : à l’intérieur d’un train Corail et dans une pièce
où deux personnes discutent. Les deux environnements sonores ont par
ailleurs été enregistrés et les documents 2 et 3 présentent les
spectres associés. Ces sons n’étant pas périodiques mais
particulièrement complexes, leurs spectres ne sont pas des spectres de
raies comme celui d’une note jouée par un instrument de musique mais
des spectres continus. L’amplitude relative en ordonnée montre la
contribution de chaque fréquence émise au niveau d’intensité sonore
global.
Prévoir
dans lequel des deux environnements sonores le dispositif actif est
susceptible d’intervenir le plus efficacement. Justifier.
Le dispositif actif atténue de 18 à 25 dB le bruit dont les fréquences
sont comprises entre 50 et 400 Hz. L'amplitude relative de ces
fréquences est très importantes dans un train corail. L'atténuation est
encore de 15 dB pour les fréquences comprises entre 500 et 1500 Hz. Ce
dispositif est bien adapté à l'environnement sonore d'un train corail.
|
.
|
|
Simulation du dispositif actif.
D’après la notice, la réduction active du bruit consiste à émettre un
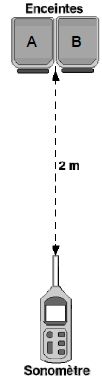
signal dit « anti-bruit ». Le dispositif expérimental représenté
ci-contre est mis en place.
Le bruit est modélisé par une onde sonore sinusoïdale de fréquence fB = 132 Hz émise par l’enceinte acoustique B.
Le signal anti-bruit est modélisé par une onde sonore sinusoïdale de fréquence fA émise par une deuxième enceinte acoustique A accolée à la première.
Un logiciel contrôle la fréquence et l’intensité de chaque signal ainsi que le déphasage entre les signaux.
À une distance de deux mètres face aux enceintes, le niveau d’intensité
sonore du son émis par chaque enceinte, seule, est systématiquement
ajusté à LA = LB = 50 dB.
Ce dispositif permet ainsi de mesurer l’influence de la fréquence de
chaque signal et du déphasage entre les signaux sur le niveau
d’intensité sonore L face aux deux enceintes à
une distance de deux mètres.
Les résultats de trois expériences sont regroupés dans le document 4 ci-après.
Expérience
|
1
|
2
|
3
|
Fréquence fB (Hz)
|
132
|
132
|
132
|
| Fréquence fA (Hz) |
198
|
132
|
132
|
Déphasage des signaux
|
|
en phase
|
en opposition de phase
|
L(dB)
|
53 ±1
|
56 ±1
|
44 ±1
|
Intervalle de confiance (Hz)
|
52 - 54
|
55 - 57
|
43 - 45
|
Les incertitudes affichées dans ce document sont associées à des niveaux de confiance de 95%.
|
|
Les
intervalles de confiance associés aux mesures des niveaux d’intensité
sonores lors des expériences 1, 2 et 3 permettent-ils de conclure que
les valeurs mesurées sont significativement différentes ? Justifier.
Les intervalles de confiance sont bien distincts ( expériences 2 et 3)
; les valeurs mesurées sont significativement différentes.
On note I l’intensité sonore associée au niveau d’intensité sonore L. Pour quelle expérience l’intensité I du son est-elle la somme des intensités des sons issus de chaque enceinte prise séparément ? On justifiera la réponse par un calcul.
IA seule = IB seule = I0 105 W m-2 ; I1 = I0 105,3 ~2 105 I0 W m-2 ; I2 = I0 105,6 ~4 105 I0 W m-2 ; I3 = I0 104,4 ~2,5 104 I0 W m-2 ;
I1 =IA seule + IB seule .
Comme les ondes
électromagnétiques, les ondes sonores peuvent donner lieu aux
phénomènes de réflexion, réfraction, diffraction, interférences, etc.
Par comparaison avec les propriétés des ondes électromagnétiques monochromatiques, indiquer quel phénomène physique est responsable de la variation du niveau d’intensité sonore observée
d’une expérience à l’autre dans le document 4. On apportera les précisions nécessaires permettant de justifier l’évolution du niveau d’intensité sonore.
Expérience 2 : les interférences sont constructives, ( onde ayant même
fréquence et en phase ), l'intensité sonore résultante est bien
supérieure à la somme des intensités sonores de chaque onde.
Expéreince 3 : les interférences sont destructives, ( ondes de même fréquence en opposition de phase )
l'intensité sonore résultante est bien inférieure à l
intensité sonore de chaque onde.
Quelle expérience modélise le dispositif actif de réduction de bruit ? Justifier votre réponse.
L'expérience 3 modèlise le dispositif actif de réduction de bruit.Le niveau sonore résultant diminue d'environ 10 dB.
|
|
|
Traitement numérique du bruit.
Le pas de quantification p d’un convertisseur sur n bits s’exprime par : DU/2n où DU est la plage de conversion exprimée en volt.
La condition de Shannon indique que, pour numériser convenablement un
signal, il faut que la fréquence d’échantillonnage soit au moins deux
fois supérieure à la fréquence maximale du signal à numériser.
Le signal anti-bruit émis résulte d’un traitement numérique du bruit selon les étapes suivantes :
(a) le bruit est capté par un microphone ;
(b) le signal électrique correspondant est numérisé ;
(c) le signal numérique est traité pour produire le signal numérique anti-bruit ;
(d) le signal numérique anti-bruit est converti en signal analogique.
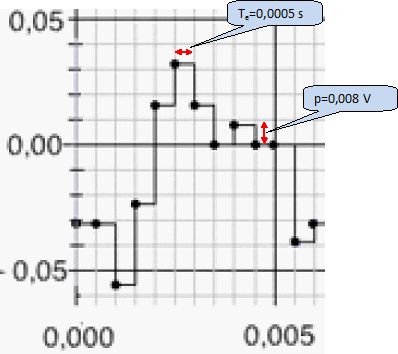
Les graphiques ci-contre illustrent, pour une fréquence d’échantillonnage fe et un pas de quantification p donnés, le début du processus de
traitement.
Calculer la fréquence fe d’échantillonnage et estimer la valeur du pas p de la quantification.
Un petit carreau correspond à 0,5 ms = 5 10-4 s ; fe = 1/(5 10-4) =2,0 kHz.
Le pas "p" en tension d'un CAN est le plus petit écart de tension entre deux points du signal numérisé : p = 0,008 V.
La plage de conversion a pour valeur ΔU = 2 V.
S’agit-il d’un codage sur 8 ou sur 16 bits ?
p = DU/2n ; 2n = DU/ p = 2 / 0,008 = 2,5 102 ; n = 8 bits.
|
|
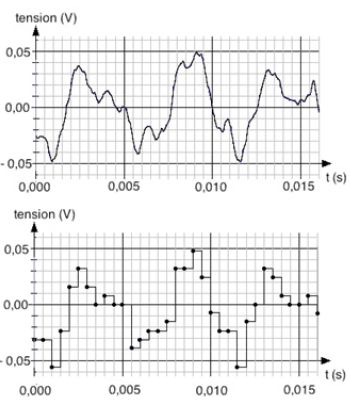
Dans
le cas du casque, le bruit est traité par séquences enregistrées de
durée 6,4 ms avec une fréquence d’échantillonnage de 20 kHz et un
codage sur 8 bits.
Calculer en bit ou en octet la taille du fichier associé à la séquence numérisée de durée 6,4 ms.
Te = 1/ (2 104 ) = 5 10-5 s ; nombre de mesures sur une durée de 6,4 ms : 6,4 10-3 / (5 10-5) =128.
Chaque mesure est codée sur 8 bits ; nombre de bits : 128*8 ~ 1,0 103 bits.
La
fréquence d’échantillonnage choisie remplit-elle la condition de
Shannon dans le cadre du traitement des bruits dont les spectres sont
donnés dans les documents 2 et 3 ? Justifier votre
réponse.
Les fréquences maximales sont inférieures à 10 kHz. La fréquence
d'échantillonnage est supérieure à 2 fois la fréquence maximale. La
condition de Shannon est bien remplie.
|
|
|






