Equipements
présents dans les laiteries, radioactivité de l'iode 131 . Bac Stl B
2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
|
|
|
|
Consommation
électrique.
Équipements
électriques présents dans les laiteries.
Les équipements électriques sont multiples. L’essentiel de ces
équipements est lié au bloc « traite»:
- le tank (ou réservoir) à lait qui permet le refroidissement du lait
et son stockage, le chauffe-eau, l’éclairage du bloc
traite, les équipements de nettoyage, les autres
postes...
Nommer
la grandeur physique à laquelle se rapporte le terme « consommation ».
C'est l'énergie électrique consommée par le tank à lait.
Donner
la relation reliant les grandeurs : puissance P, énergie E mise en jeu
durant Δt
et en indiquant pour chacune l’unité dans le système international
d’unités.
E = P Dt
avec E en joule, P en watt et Dt
en seconde.
Calculer
la consommation électrique moyenne annuelle du tank ramenée à une vache
laitière.
Consommation totale diminuée de celles des autres postes =
420-(11+21+3+14+8+10+68+120)=165 kWh par vache.
Refroidissement
du lait.
Le refroidissement du lait et son stockage ont lieu dans le tank (ou
réservoir) à lait. Lorsque la température du lait varie d’une valeur
initiale θi
à une valeur finale θf,
l’énergie échangée sous forme de chaleur Q par le lait avec le tank est
égale à la variation de son énergie interne ΔU. On a la
relation suivante : Q = m lait C lait
( qf- qi).
Calculer
l’énergie échangée sous forme thermique avec le tank pour 300 litres de
lait de masse 310 kg quand ils passent de la température
initiale θi à la température finale θf.
Données : θi
= 35 °C, θf
= 4 °C, C lait = 3,8 × 10 3
J.kg –1.°C –1 , 1 kW.h =
3,6 × 10 6 J.
Q = 310*3,8 10 3 *(4-35) =-3,65 10 7
J ou -3,65
107 /(3,6 × 10 6)~ -10 kWh.
Vérifier
que pour une durée de fonctionnement de Δt = 4,0 h, la
puissance mise en jeu est P = 2,5 kW.
Energie électrique consommée( kWh) divisée par la durée en
heure = 10/4 = 2,5 kW.
Déplacement
d’échantillons de lait à l’aide d’un mini-convoyeur.
Après refroidissement et traitements biologiques spécifiques à la
conservation, des échantillons de lait sont prélevés afin d’être
analysés et contrôlés. Les pots contenant ces échantillons sont
déplacés à l’aide d’un tapis roulant appelé mini-convoyeur.
Analyse
électrique.
Des moteurs à courant continu équipent les mini-convoyeurs et assurent
des performances optimales.
 Préciser
la valeur de la tension d’alimentation U pour le mini-convoyeur
installé, et celle de la puissance P absorbée par le moteur
Préciser
la valeur de la tension d’alimentation U pour le mini-convoyeur
installé, et celle de la puissance P absorbée par le moteur.
U = 24 V et p = 36 W.
Pour
le type de moteur utilisé, donner la relation liant les grandeurs P et
U précédentes, à l’intensité I du courant. Indiquer leurs unités dans
le système international.
P= U I avec P en watt, U en volt et I en ampère.
Calculer
la valeur de l’intensité I du courant.
I = P/U = 36/24 = 1,5 A.
Analyse
énergétique.
Le moteur électrique est un convertisseur d’énergie.
Compléter
le document suivant, en précisant sur le diagramme de la chaîne
énergétique, les types d’énergie mis en jeu.
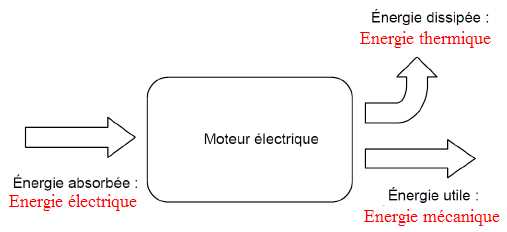 Le rendement h =Pméca
/ Pélec de ce type de moteur est de 95 %. Exprimer
puis calculer la puissance mécanique Pméca
disponible.
Le rendement h =Pméca
/ Pélec de ce type de moteur est de 95 %. Exprimer
puis calculer la puissance mécanique Pméca
disponible.
Pméca = 0,95 *36 =34,2 ~34 kW.
Mise
en mouvement de la bande du tapis roulant du mini-convoyeur.
La bande du tapis roulant est mise en mouvement par le moteur
électrique précédent.
Pour
une charge de 30 N, indiquer la valeur v de la vitesse linéaire du tapis.
le document ci-dessus indique 8,0 m / min soit 8,0 /60 =0,133 ~0,13 m/s.
Le
tapis est entraîné par des galets de rayon R = 2,0 cm tournant à la
vitesse angulaire w.
Exprimer
ω en
fonction de v et de R, puis calculer sa valeur.
w
= v/R = 0,133 / 0,02 = 6,67 ~6,7 rad/s.
|
|
|
Analyse mécanique
Un pot contenant l’échantillon de lait est présent sur ce tapis. Le
tapis est incliné.
Dans un premier temps, le tapis est immobile.
Réaliser
l’inventaire des forces s’exerçant sur le pot. Représenter
ces forces (sans tenir compte de l’échelle).
Le poids du pot et l'action du tapis ( action perpendiculaire au plan
et frottements ).
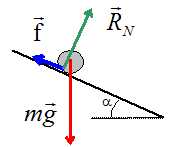
Quelle
relation vectorielle existe-t-il entre ces différentes forces ?
Justifier la réponse.
Le pot est immobile, la première loi de Newton indique que la somme
vectorielle des forces est nulle.
Gestion
des fluides.
Les échantillons de lait, non conformes aux analyses, sont stockés dans
une cuve.
L’évacuation de ces déchets de lait est réalisée vers une canalisation
extérieure par l’intermédiaire d’un tuyau de section S = 5,00 x 10–4
m2, placé en bas de la cuve. Le temps nécessaire
à la vidange d’un volume V = 120 L est de Δt = 10,0 minutes.
Exprimer le débit volumique QV en fonction de V
et Δt,
puis le calculer en l’exprimant en L.min–1, puis
en m3.s–1.
QV
= V / Δt = 120 / 10,0 =
12,0 L /min ou 0,120 / 600=2,00 10-4 m3
s-1.
Quand la cuve est pleine, la hauteur de lait est de 1,50 m.
Citer
le principe fondamental de l’hydrostatique permettant d’exprimer la
variation de pression ΔP entre le
haut et le bas de la cuve, en fonction de la masse volumique du lait ρlait,, de la
hauteur de lait hlait et de
l’intensité de la pesanteur g. Calculer cette variation de pression ΔP.
La différence de pression entre deux points d'un liquide homogène est
proportionnelle à la masse volumique du liquide, à l'accélération de la
pesanteur et à la différence de niveau entre ces deux points.
DP
= rlait
g hlait = 1,03 103
*9,80*1,50 =1,51 104 Pa.
|
.
|
|
Contrôle
et analyse des échantillons de lait.
L’état de fraîcheur d’un lait est contrôlé en mesurant son acidité
totale en acide lactique. En effet, un lait frais ne contient pas
d’acide lactique, mais au cours du temps les bactéries lactiques
présentes dans le lait provoquent la transformation d’une partie du
lactose en acide lactique. Le lait devient alors de plus en plus acide.
L’acide lactique a pour formule : CH3–CHOH–COOH.
Détermination
de la concentration en acide lactique.
Un dosage suivi par pH-métrie est réalisé sur un échantillon de lait.
Le réactif titrant utilisé est une solution d’hydroxyde de sodium (Na+(aq),
HO–(aq)), de concentration cb
égale à 0,25 mol.L–1.
Donner
la définition d’un acide.
Un acide est une espèce susceptible de libérer un proton H+.
Préciser
les équipements de protection individuels (E.P.I.) à utiliser pour
manipuler ce réactif.
La solution étant corrosive, port de gants, lunette et blouse.
Écrire
l’équation de la réaction entre l’acide lactique et l’hydroxyde de
sodium en solution.
CH3-CH(OH)-COOHaq + HO-aq
---> CH3-CH(OH)-COO-aq
+ H2O.
Incertitude
liée au dosage.
Afin de s’assurer de la valeur des résultats obtenus, différents
dosages sont réalisés sur le même échantillon.
Les mesures de la concentration C en acide lactique trouvées
expérimentalement permettent de calculer la moyenne Cmoy
= 411 mmol/L et l'écart type s
= 5,68 mmol/L.
L’incertitude associée au mesurage est notée U(C). C’est une grandeur
définissant un intervalle autour du résultat de mesurage. Elle est
associée à un niveau de confiance. Elle s’exprime sous la forme :
U(C) = t(n, x%) s / n½.
Pour n = 10 mesures, t(10,0,95) = 2,23.
En
déduire la valeur U(C) de l’incertitude associée au mesurage.
U(C) =2,23 *5,68 / 10½ =4,00 mmol/L.
En
déduire l’écriture du résultat de la concentration C en précisant
l’unité et le niveau de confiance de l’intervalle estimé.
C = 411 ±4 mmol/L avec un niveau de confiance de 95 %.
Radioactivité
du lait à la suite de l’accident de Fukushima.
Donner
le nom et la notation symbolique de l'iode 131 ( Z = 53). 13153I.
Définir
la notion d’isotopie. Donner les différents isotopes de l’iode I.
Deux isotopes ne diffèrent que par leur nombre de neutrons. Ils ont le
même numéro atomique Z.
12353I ; 12753I
; 13153I.
L’iode 131 est radioactif β–.
Donner
la notation symbolique et le nom de la particule β–.
Il s'agit d'un électron noté 0-1e.
Ecrire
l’équation de désintégration de l’iode 131 et préciser la notation
symbolique du noyau fils obtenu.
13153I
---> 13154Xe + 0-1e.
Donner
la définition de la demi-vie t1/2 (également
noté T).
La demi-vie est la durée au bout de laquelle l'activité initiale est
divisée par deux.
La demi-vie de l'iode 131 est t½ = 8 jours.
Le document suivant représente la courbe de décroissance radioactive de
l’iode 131, pour un litre de lait. Indiquer sur ce document :
- le nom et le symbole de la grandeur exprimée en becquerel,
- les durées t1/2, 2 t1/2,
3 t1/2 (durées également notées T, 2 T et 3 T).
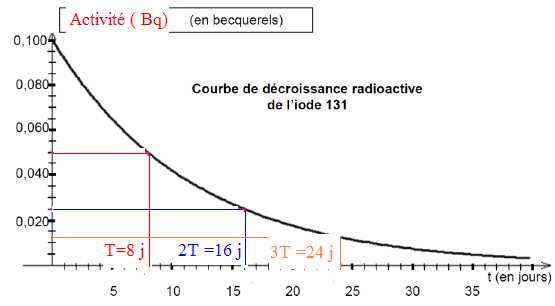
Déduire
de ce graphe, ou d’un raisonnement, la valeur de l’ordonnée exprimée en
becquerels, mesurée au bout de 32 jours.
Au bout de 32 jours, soit 4 demi-vie ou période, l'activité initiale
est divisée par 24 = 16 : 0,100 /16 = 0,00625 Bq.
Une
partie du rayonnement peut être absorbée par l’organisme humain.
La dose d’énergie absorbée D est égale à : D = E/m.
Avec E : énergie transférée en joules (J), m : masse de
matière irradiée (kg), D : dose d’énergie absorbée
Citer
l’unité de mesure de la dose d’énergie absorbée D.
Joule / kilogramme ( J kg-1).
Pour un litre de lait absorbé, un enfant de masse m = 10 kg reçoit une
énergie E = 0,0010 J.
Calculer
la dose d’énergie D absorbée par cet enfant.
D = 0,0010 / 10 = 1,0 10-4 J kg-1.
Citer
un risque lié pour l’organisme humain lié à la radioactivité.
Développement de cancers.
|
|
|