Mathématiques :
équation différentielle, étude de fonction, calcul intégral,
probabilité ( groupe
B), bts 2010.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
|
|
|
|
|
Résolution
d'une équation différentielle.
On considère l'équation différentielle (E) : y'-y = ex-2x.
où y est une fonction inconnue de la variable x, définie et dérivable
sur R et y' sa fonction dérivée.
Déterminer les solutions de l'équation différentielle (E0)
:
y'-y=0.
y = A eBx avec A et B des constantes réelles.
Dériver : y' = ABeBx ; repport dans E0 : ABeBx -A eBx =0.
AeBx (B-1)=0 d'où B = 1 ; par suite y = A ex.
Soit g la fonction définie sur R par g(x) = x ex+2x+2.
Démontrer que la fonction g est une solution particulière de (E).
On pose u = x ; v = ex ; u' =1 ; v' =ex ;
Dérivée de x ex : u'v + v'u =ex +x ex =ex (x+1).
Par suite g' = ex (x+1)+2.
Repport dans (E) : ex (x+1)+2-( x ex+2x+2) =ex-2x.
Simplifier : ex -2x = ex-2x. Cette égalité est vérifiée quel que soit x.
En déduire
l'ensemble des
solutions de (E).
Les solutions de (E) sont obtenues en faisant la somme des solutions de
(E0) et d'une solution particulière de (E) :
y = A ex+ x ex+2x+2.
Déterminer
la
solution f de l'équation différentielle (E) qui vérifie la condition
initiale f(0)=3.
f(0) = A e0+2 = 3 ; A+2=3 ; A=1.
f(x) = ex +x ex+2x+2 = (1+x)ex +2(x+1) = (x+1)(ex+2).
|
| .
. |
|
|
Etude d'une fonction et calcul intégral.
Soit f la fonction définie sur R par f(x) =(1+x)ex +2x+2. On note C sa courbe représentative dans le plan muni d'un repère orthogonal.
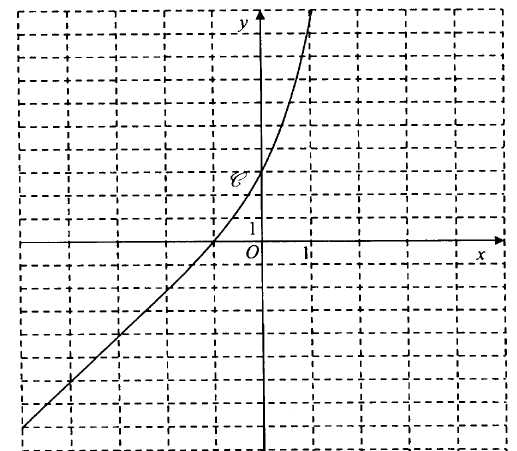
Calculer la limite de f(x) quand x tend vers l'infini.
Quand x tend vers l'infini :
(1+x)ex tend vers l'infini ; 2x tend vers l'infini : f(x) tend vers l'infini.
La courbe C admet une asymptote en moins l'infini. Quelle est son équation ?
Quand x tend vers moins l'infini : ex tend vers zéro ; l'exponentielle étant prépondérante devant un polynome :
(1+x)ex tend vers zéro. La droite d'équation y = 2x+2 est donc asymptote.
Démontrer que le
développement limité, à l'ordre 2, au voisinage de zéro, de
la fonction f est :
f(x)=3 + 4x +1,5 x2+x2e(x).
Le développement
limité à l'ordre 2, au voisinage de zéro, de la fonction h(x) = ex
est :
h(x) = 1 +x +½x2 + x2e(x).
f(x) =(x+1) ex+2x+2 = (x+1)(1 +x +½x2 + x2e(x))+2x+2.
Développer en se limitant à l'ordre 2 : f(x)= x +x2+1+x+½x2+ x2e(x)+2x+2.
Simplifier : f(x)= 3+ 4x +1,5x2+ x2e(x).
En
déduire une équation de la tangente T à la courbe C au point d'abscisse
x=0.
y = 3+4x.
Etudier la
position
relative de T et C au voisinage du point d'abscisse 0.
Au voisinage de zéro, f(x)-y = +1,5 x2 .
f(x)-y
est positif ; f(x) > y : la
tangente est située en dessous de la courbe C.
|
.
|
|
On note : 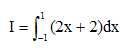 . Montrer que I = 4. . Montrer que I = 4.
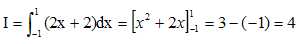
On note : 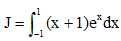
Démontrer à l'aide d'une intégration par parties que J = e + e-1.
On pose u = x+1 et v' = ex ; u' =1 et v=ex.
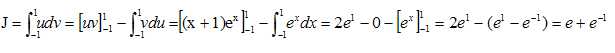
On note :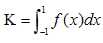
Déduire la valeur exacte de K puis sa valeur à 0,01 près.
K = I+J = 4 + e + e-1 = 4+2,718 +0,3679 =7,086 ~7,09.
Interpréter
graphiquement le nombre K.
K est l'aire ( exprimée en unité d'aire) comprise entre la courbe C et
l'axe horizontal, comptée positivement.
Dans une usine de conditionement, une machime remplit à la chaîne des bouteilles d'un certain liquide.
Loi binomiale et loi de Poisson.
On
note E l'évènement " une bouteille prélevée au hasard dans un stock
important est non conforme au cahier des charges". On suppose que la
probabilité de E est p = 0,02.
On prélève au hasard 30 bouteilles
dans le stock pour vérification. On suppose que le stock est
suffisamment important pour qu'on puisse assimiler ce prélèvement à un
tirage avec remise.
On
désigne par X la variable aléatoire qui, à chaque prélèvement de 30 bouteilles, associe le nombre de bouteilles non conformes.
Justifier
que X suit une loi binomiale dont on précisera les paramètres.
Les prélevements sont indépendants et leur nombre est fixé à n = 30.
Chaque
tirage peut déboucher seulement sur 2 résultats : la
probabilité qu'une bouteille soit non conforme est constante p = 0,02. La
probabilité qu'une bouteille soit conforme est q = 1-p = 0,98.
La loi binomiale B(n=30, p = 0,02) est valide.
Calculer P(X <=1).
P(X=0)=C300 p0
q30 avec C300
= 1 ;
P(X=0)= 0,9830 =0,54548.
P(X=1)=C301 p1
q29 avec C301
= 30 ;
P(X=1)=30*0,02* 0,9829 =0,33397.
P(X=0)+
P(X=1) =0,54548 +0,33397 =0,8794 ~0,879.
On considère que la loi de probabilité suivie par la variable aléatoire X peut être approchée par une loi de Poisson.
Quel est le paramètre de cette loi de Poisson ? l = np = 30*0,02 =0,6.
On désigne par Y une variable aléatoire suivant a loi de Poisson de paramètre l.
Calculer la probabilité que dans un tel prélèvement de 30 bouteilles, au plus une bouteille soit non conforme.
"au plus une bouteille" signifie 0 ou 1.
Les tables donnent :
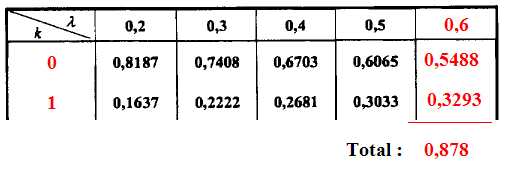
|
Loi normale.
On considère une grande quantité de bouteille devant être livrées à des clients
On
désigne par Z la variable aléatoire qui, à une bouteille prélevée au
hasard dans cette livraison, associe sa contenance en centilitres. On
admet que Z suit la loi normale de moyenne 70 et d'écart type 1.
Déterminer
la probabilité P(68 <= Z <=72).
X suit la loi normale N(m=70, s=1).
p(68<=Z<=72) = p(-2 < = (X-m) / s <=2)
(Y-m) / s
suit la loi normale centrée
réduite : 2P(2)-1.
Les tables donnent P(2)= 0,9772 et 2P(2)-1 = 2*0,9772-1 =0,9544 ~0,95.
Déterminer le nombre réel h positif tel que P(70-h <=Z <=70+h) =0,99.
2P(t)-1 = 0,99 ; P(t) =1,99/2 =0,995.
Les tables
donnent t = 2,575.

L'intervalle de confiance est donc : [70-2,575 s ; 70+2,575 s ] soit h = 2,575 s =2,575*1 = 2,575~2,58.
La probabilité qu'une bouteille est un volume compris 67,4 L et 72,6 cL est 0,99.
Intervalle de confiance.
Une chaine de supermarchés réceptionne un lot important de bouteilles dont elle souhaite estimer la contenance moyenne.
On prélève
au hasard avec remise un échantillon de 100 bouteilles dans ce lot.
Soit C la variable aléatoire qui, à tout échantillon de 100 bouteilles ainsi
prélevé, associe la moyenne des contenance en cL de cet échantillon.
On suppose que C suit la loi normale de moyenne inconnue p et d'écart
type s=0,1.
Pour l'échantillon prélevé, la moyenne est x=70,12.
Déterminer
un intervalle de confiance centré en x de la moyenne µ des contenances
des bouteilles de ce lot, avec le coefficient de confiance de 95 %.
C suit
la loi normale N(p, s).
F0=(F-p)
/ s suit
la loi normale centrée
réduite.
p(-t < F0 < t) =0,95 ; 2P(t)-1 =0,95
; P(t) =1,95/2 =
0,975.
Les tables
donnent t = 1,96.

L'intervalle de confiance est donc : [x-1,96 s ; x+1,96 s ] soit
[70,12-1,96*0,1 ; 70,12+1,96*0,1] soit [ 69,92 ; 70,32].
On
considère l'affirmation suivante : " la moyenne µ est obligatoirement
dans cet intervalle de confiance".
Cette
affirmation est-elle vraie ?
Cette affirmation est fausse. Dans 95 % des cas, µ se trouve
dans cet intervalle de confiance.
|
|