Mathématiques : calcul intégral, bts
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
|
|
|
|
|
Calcul
intégral.
On
note 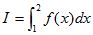 où f est
définie dans la partie précédente. où f est
définie dans la partie précédente.
Démontrer,
à l'aide d'une intégration par partie, que I = (23 e-4-13e-2)
/ 4.
On pose : u = 1-5x ; v ' =exp(-2x) ; u'= -5 ; v = -½ exp(-2x).
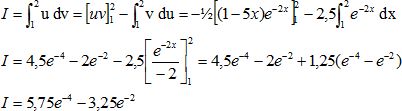
Donner
la valeur approchée de I à 0,01 près.
I = 5,75 *0,01831 -3,25*0,1353= -0,33.
Donner,
sans justification, le signe de f(x) pour x dans l'intervalle [1, 2].
Le terme en exponentielle est positif et (1-5x) est négatif : f(x) est
donc négative.
Interpréter
graphiquement le nombre I.
I est l'aire ( exprimée en unité d'aire) comprise entre la courbe C et
l'axe horizontal, comptée négativement.
Calcul
intégral.
On
note 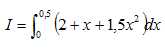 . .
Démontrer que I =1,1875.
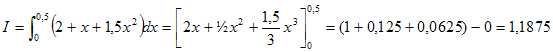
On note 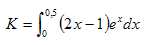
Démontrer,
à l'aide d'une intégration par partie, que K= 3-2e0,5.
On pose : u = 2x-1 ; v ' =ex ; u'= 2 ; v =ex.
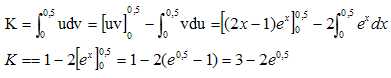
On note 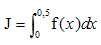
Déterminer la valeur exacte de J.
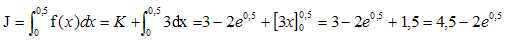
Vérifier que J-I est inférieure à 0,02.
4,5-2e0,5-1,1875=0,015.
|
| .
. |
|
|
Soit f la fonction définie sur R par f(x) =(1+x)ex +2x+2.
On note : 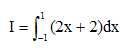 . Montrer que I = 4. . Montrer que I = 4.
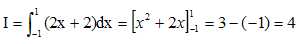
On note : 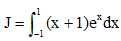
Démontrer à l'aide d'une intégration par parties que J = e + e-1.
On pose u = x+1 et v' = ex ; u' =1 et v=ex.
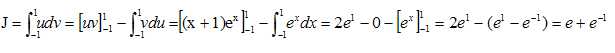
On note :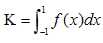
Déduire la valeur exacte de K puis sa valeur à 0,01 près.
K = I+J = 4 + e + e-1 = 4+2,718 +0,3679 =7,086 ~7,09.
Interpréter
graphiquement le nombre K.
K est l'aire ( exprimée en unité d'aire) comprise entre la courbe C et
l'axe horizontal, comptée positivement.
|
.
.
|