L'oxyde de calcium, la zircone. Agrégation. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . Le cristal d'oxyde de calcium. C'est un cristal ionique qui cristallise dans le système de type chlorure de sodium.. Donner la structure électronique à l'état fondamental de l'atome de calcium, après avoir énoncé les règles qui permettent de l'établir. Règle de Pauli : deux électrons se différencient par au moins l'un de leur nombres quantiques n, l, m et s. Règle de Klechkowski : l'ordre de remplissage des orbitales se fait suivant (n+l) croissant ; si deux orbitales atomiques ont le même nombre (l+n), celle qui a la plus faible valeur de n est remplie en premier ( principe de stabilité) 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f... Règle de Hund : cas des orbitales de mêmes énergie. Les électrons de spins parallèles occupent le maximum d'orbitales. 20 Ca : 1s2 2s2 2p6 3s2 3p6 4s2 . L'atome de calcium perd facilement  deux électrons et donne l'ion Ca2+ dans lequel la couche électronique externe est complète. Le nombre d'oxydation du calcium dans l'ion calcium est +II, égal à la charge de l'ion simple. 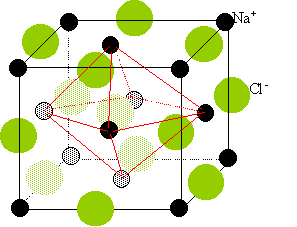Représenter la maille de CaO. cristaux type NaCl : Deux réseaux cubiques à faces centrées, l'un d'ion Na+, l'autre d'ion chlorure Cl-. Ces réseaux se déduisent l'un de l'autre par translation parallèle aux arètes de la maille et de valeur égale à la moitié du coté de la maille. Chaque ion est au centre d'un octaèdre, entouré de 6 ions de signe opposé occupant les 6 sommets. Déterminer le nombre d'ions présents dans  la maille CaO. Déterminer le nombre de motifs par maille. Chaque ion situé au sommet du cube est commun  à huit mailles, il compte pour 1/8. Les ions situés sur les huit sommets comptent pour 1/8 *8 = 1. Chaque ion situé au centre d'une face est commun  à 2 mailles : il compte pour 1/2. Les 6 ions situés aux centres des 6 faces  comptent pour 1/2*6 = 3. Il y a donc 4 ions calcium et 4 ions oxyde par maille. Définir la coordinence. C'est le nombre d'ions de signe opposé entourant chaque ion, il est ici de six. Chaque ion peut être considéré comme étant au centre d'un octaèdre dont les six sommets sont occupés par des ions de signe opposé. Etablir la relation littérale permettant d'accéder à la masse volumique r du cristal CaO. Calculer sa valeur. Paramètre de la maille a = 481 pm ; rayon du cation r+ =99 pm. La maille compte en propre 4 motifs CaO. masse de la maille : 4 * masse molaire CaO (kg/mol) / nombre d'Avogadro  m = 4 MNaCl / NA. volume de la maille V =a3. (en m3) masse volumique (kg/m3 ) : r = m /V=4 MCaO / (a3NA) r =4*56 10-3 / ((481 10-12)3 * 6,023 1023) =3,34 103 kg/m3. . . Déterminer une relation entre les rayons ioniques et le paramètre de la maille. Calculer r. a = 2(r+ + r-) ; r-= ½a - r+ =481/2 -99 =141,5 ~142 pm. Définir puis calculer la compacité du cristal. C'est le rapport entre le volume occupé par les ions et le volume de la maille. Volume des ions ( sphère) : 4 *4*p /3[r-3+r+3] Volume de la maille: a3 ; compacité : C = 4 *4*p /3[r-3+r+3] / a3  C = 16*3,14/3 [141,53 + 993] 10-36 / (481 10-12)3 =0,572. . La sonde « zircone ». Il est souvent nécessaire de mesurer la concentration en dioxygène de milieux portés à hautes températures (gaz d’échappement, métaux fondus, etc…). On utilise pour cela la conductivité ionique de la zircone stabilisée. La zircone ZrO2 cristallise à très haute température (T ≥ 2370°C) dans une structure de type fluorine CaF2. Dans cette structure, les ions Zr4+ forment un réseau cubique à faces centrées dont les sites tétraédriques sont occupés par les ions O2-. Faire un schéma en perspective de la maille de la zircone et préciser par des représentations en coupe les positions des différents ions dans la maille. Les ions Zr4+ ocupent les sommets du cube et le centre de chaque face ; les ions O2-occupent les 8 sites tétraèdriques. Déterminer les coordinences anion/cation et cation/anion. Chaque anion est au centre d'un tétraèdre dont les sommets sont occupés par quatre cations. Chaque cation est au centre d'un cube dont les sommets sont occupés par huit anions. Identifier les sites laissés vacants dans le cristal. Les sites octaèdriques (Il y en a 4 par maille; ils sont situés au centre de la maille et aussi au milieu des arètes ) sont inoccupés. Calculer la masse volumique attendue pour ce solide. La maille compte 8 anions O2- et 4 cations Zr4+ soit 4 motifs ZrO2. Masse de la maille m = 4M(ZrO2)/N =4*(91,2 +2*16,0) 10-3 / (6,02 1023) =8,185 10-25 kg. Volume de la maille V = a3 =(509 10-12)3 = 1,319 10-28 m3. Masse volumique r = m/V = 8,185 10-25 / (1,319 10-28)~6,21 103 kg m-3. Rappeler les hypothèses sur lesquelles repose le modèle du cristal ionique parfait. Lesions sont des sphères dures. Les ions les plus petits s'insèrent dans les sites du réseau constitué par les plus gros. Seuls les  ions de signe différent sont en contact. Déterminer la valeur minimale que doit prendre, dans ce modèle, le rapport des rayons ioniques pour que cette structure existe. Commenter le résultat. Dimension de la grande diagonale du petit carré rouge ( figure ci-dessous) : d2= (½a)2 + (½2½a)2 ; d = 3½ a/2 . On donne rZr4+ = 84 pm et rO2- = 138 pm. rZr4+ /rO2- =84/138 ~ 0,61. La condition ci-dessus n'est pas respectée. Le cristal ne peut pas être décrit par le modèle du crital ionique parfait. Il est possible de stabiliser cette structure à basse température en y incorporant de 15 à 28% d’oxyde de calcium CaO, l’ion Ca2+ venant occuper dans le cristal la même position que l’ion Zr4+. On constate alors que le cristal obtenu devient un conducteur ionique. Montrer que l’introduction de Ca2+ et O2- dans le cristal entraîne la création de lacunes. En remplaçant Zr4+ +2O2- par Ca2+ + O2-, on créé un déficit en ion oxyde. Proposer une équation traduisant l’incorporation de CaO au cristal. CaO --->  Ca2+ + O2- + lacune en Oxyde  Donner une interprétation de la conduction dans ce cristal. Le nombre de lacunes est égal au nombre d'ion calcium. Les ions oxydes peuvent migrer de lacune en lacune. .

menu