Les fluides, notion de pression,
poussée d'Archimède :
Agrégation interne 2014.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
|
|
|
|
|
|
|
Un système
fluide monophasé, est décrit comme un système à trois échelles de
longueur.
Dans le cas d'un liquide et d'un gaz à pression et température ambiante
: Citer
celles-ci.
En
s’appuyant sur une situation concrète, donner une valeur numérique
caractéristique pour chacune de ces échelles.
Echelle
microscopique : en phase condensée, taille des molécules ( 0,1
nm ) ; pour un gaz, libre parcours moyen ( quelques nanomètres).
Echelle
macroscopique : taille du récipient contenant le fluide, échelle
humaine ( de l'ordre du mètre ).
Echelle
mésoscopique
: échelle intermédiaire entre les deux précédentes. Le volume de fluide
doit être suffisamment grand pour apparaître comme un milieu continu et
assez petit pour que les grandeurs intensives soient constantes.
( du micromètre à quelques dizaines de micromètres ).
Afin de modéliser les interactions intermoléculaires, il est parfois
fait usage en physique statistique d'un potentiel intermoléculaire V(r)
de type Lennard-Jones : V(r) = E 0[ (r 0/r) 12-2(r 0/r) 6].
r représente la distance intermoléculaire de deux molécules supposées
ponctuelles et E 0 une constante positive.
Justifier
en quoi ce potentiel permet de modéliser un gaz réel.
Les molécules d'un gaz réel
interagissent entre elles ; (r0/r)6 terme attractif dominant à grande distance,
tenant compte les interactions de van der Waals.
de plus elles ne sont
pas ponctuelles : (r0/r)12
: terme répulsif dominant à courte distance, les nuages électroniques
de deux atomes ne peuvent pas interpénétrer.
Proposer une
explication accessible à un élève de terminale S permettant de
comprendre l'expression de la densité critique.
Une densité, notée n , est inversement proportionnelle à un volume,
c'est à dire à une longueur au cube.
En physique
quantique : on compare la distance inter-atomique à la longueur
d'onde de de Broglie l = h/p
avec p quantité de mouvement ; p = (2mEc)½ ; Ec
= 1,5 kBT.
l = h (3mkBT)-½
et n ~1/l3 =(3mkBT)-1,5
/h3.
Si cette longueur d'onde est comparable au libre parcours moyen d'une
particule, les effets quantiques commencent à être importants.
En
vous aidant éventuellement d’un schéma, décrire en 10 lignes maximum,
une expérience de cours destinée à une classe de seconde permettant
d'aborder la notion de forces pressantes et de pression due à l'air
ambiant.
Expérience de la
canette de soda :
Verser un peu d'eau dans la canette ; chauffer l'eau afin de la
transformer en vapeur et chasser l'air intérieur ; retourner la canette
dans le cristallisoir rempli d'eau froide ; la vapeur d'eau contenue
dans la canette se condense et il ne reste que du vide dans la canette
; elle s'écrase sous l'effet de la pression atmosphérique.
Ballon de
baudruche fermé dans une cloche à vide :
Mettre en marche la pompre à vide durant une minute puis isoler
la cloche.
le ballon se gonfle : les forces pressantes exercées par l'air
intérieur au ballon étant supérieures à celles exercées par l'air
contenu dans la cloche. De plus il est impossible de désolidariser la
cloche de son support.
Ouvrir la valve et laisser rentrer l'air dans la cloche : le ballon se
dégonfle et on peut retirer la cloche de son support.
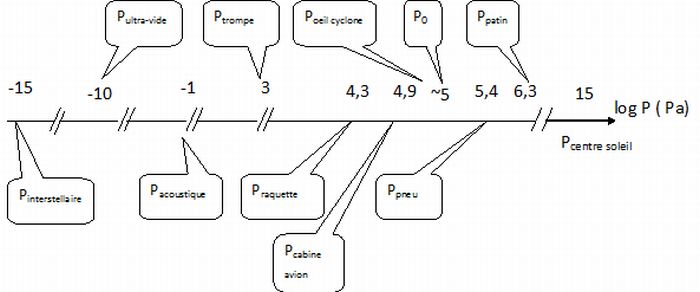
Déterminer,
évaluer ou citer, puis placer sur un axe gradué les pressions suivantes
:
pression atmosphérique par beau temps : P 0 ~1 bar ou 10 5
Pa ;
pression de gonflage d'une roue de voiture : Proue ~2 bar ou 2 105
Pa ;
pression à la sortie d'une trompe à eau : P trompe ~ 10 hPa
ou 10 3 Pa ;
pression sous 1 m d'eau : P sous1m eau =1,1 bar ;
pression dans l'oeil d'un cyclone : P oeil cyclone ~0,9
bar ;
pression exercée sur la neige par une raquette de randonnée : P raquette
= poids de la personne / surface raquette ~ 700 / 0,03 ~2 10 4
Pa ~0,2 bar ;
pression exercée par une lame de patin à glace : P patin = poids de la personne / surface
patin~ 700 / 0,0003 ~2 106 Pa ~20 bar ;
pression dans une cabine d'avion : P cabine avion ~0,8
bar ;
pression au centre du Soleil : P centre soleil ~10 15
bar ;
pression sanguine : P sanguine ~ 13 cm Hg ~0,2 bar ;
pression acoustique : P acoustique ~ 0,1 Pa ( cas d'un
aspirateur ) ;
pression de l’ultra-vide : P ultra-vide ~10 -10 Pa
;
pression du vide interstellaire : P interstellaire ~ 10-15 Pa.
|
| .
. |
|
|
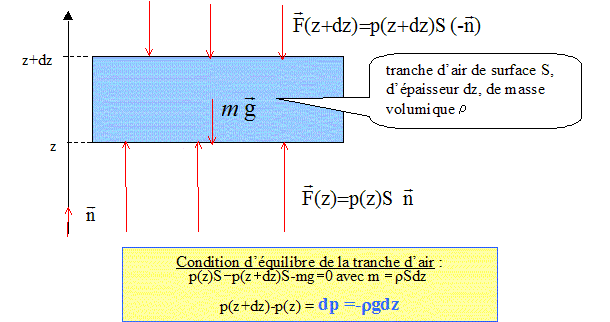
En
raisonnant sur un élément de volume de fluide homogène de forme
parallélépipédique placé dans un champ de pesanteur, établir la
relation vectorielle liant, à l’équilibre, le gradient de la
pression P à la masse volumique μ du fluide et à l’accélération du
champ de pesanteur.
Dimensions mésoscopiques du parallèlépipède : dx, dy, dz. A cette
échelle, la masse volumique peut être considérée comme constante.
Dans le
référentiel galiléen du laboratoire, ce système est soumis à son poids
et aux forces de pression exercées sur les six faces. Les forces
pressantes exercées sur les faces latérales sont deux à deux opposées.
|
.
|
|
Au sommet de l'Everest et par
beau temps, la température est qsommet
au sommet et la pression Psommet.

Proposer
un modèle quantitatif permettant d'expliquer l’évolution de la pression.
L'air est supposé être un gaz pafait ; la masse volumique de l'air
n'est pas uniforme : r = PM
/ (RT).
Entre 0 et 10 km, T(z) =a z + b avec a = (223-288) / 10 = -6,5 K km-1
= -6,5 10-3 K m-1et b = 288 K.
Ecrire la loi fondamentale de l'hydrostatique sur un axe vertical
ascendant : dP/dz = -PMg
/ (R(az+b))
dP / P = -Mdz /
(R(az+b)) ; ln P = -Mg/(aR) d( az+b) / (az+b).
ln P = -Mg/(aR) ln
( az + b) + constante.
Au sommet : PS =250 mmHg = 0,250*13600*9,81 =3,33 104
Pa ;
Constante
= ln PS +Mg/(aR) ln ( azS +
b) ;
ln P = -Mg/(aR) ln ( az + b) + ln PS +Mg/(aR) ln ( azS + b)
;
ln (P / PS) = -Mg/(aR) ln [( az + b) /( azS + b) ]
Justifier que l’on
parle de « la pression » et de « la température » à l’échelle d’une
salle de classe.
L'air de la salle est pratiquement isotherme et sa masse volumique est
constante.
On note DP, la variation de
pression entre le sol et le plafond d'altitude voisine de zS=3
m.
Ecrire la loi
fondamentale de l'hydrostatique sur un axe vertical ascendant : dP/dz =
-PMg / (RT).
dP/P = -Mg dz/ (RT)
; ln P = -Mg z / (RT) + Constante.
Constante = ln
Pplafond +Mg
zS / (RT) ; ln (P/Pplafond) = Mg / (RT) (zS-z)
= 0,029*9,8 *3 /(8.31*293)=1,2 10-4. P/Pplafond ~
1,00.
Commenter
la phrase souvent citée : « En plongée on rencontre un bar tous
les 10 m. »
Appliquer la loi fondamentale de l'hydrostatique : P = Patm +reau g h ; P - Patm = reau g h
~1000*10*10 = 105 Pa = 1 bar.
On a nommé « pascal » l'unité de pression. Indiquer à quel
siècle vécut Blaise Pascal et citer une expérience qu’il a réalisée.
Pascal a vécu au 17ème siecle.
L'expérience du Puy de Dôme prouve l'existence de la pression
atmosphérique ; la pression hydrostatique est illustrée par
l'expérience du tonneau de Pascal ; la presse hydraulique.
Une montagne typique est composée de roches de type silicate de masse
volumique rsilicate =
2,5 103 kg m-3. Une telle roche ne peut pas
supporter une pression supérieure à Pmax = 6,5 103
bar.
Proposer
un modèle permettant d'obtenir un ordre de grandeur pour la hauteur
maximale hmax d'une montagne.
La masse rocheuse est considérée comme un fluide ; on applique le loi
fondamentale de l'hydrostatique :
Pmax - Patm = rsilicate
g hmax ; hmax
= (6,5 103-1)105 / (2,5 103*9,8) = 2,6
104 m ~26 km.
Exposer
en une dizaine de lignes, une utilisation, dans le cadre du
programme de la classe de seconde générale et technologique, de la
situation déclenchante décrite sur le document suivant :
Lors d’une mission
scientifique en vue d’explorer la faune et la flore de la fosse des
Mariannes, le sous-marin dénommé « Yellowsubmarine » progresse et
s’enfonce dans des eaux noires et froides de l’océan. Ce sous-marin
peut supporter des pressions jusqu’à 500 bars. Dans la salle de
commande, le capitaine vérifie les différents afficheurs lui indiquant
la pression, la profondeur, la vitesse… Le manomètre indique une
pression de 413 bars (tout va bien !!!). L'exploration peut se
poursuivre et le capitaine décide de poursuivre la descente. Un peu
plus tard le manomètre indique 493 bars et le sonar situe la zone de la
plaine abyssale à
étudier encore 60 m plus bas. Le sous-marin pourra-t-il se poser, sans
risque, pour effectuer des prélèvements de roches ? Adaptation d'une
activité sur internet proposée en lycée professionnel.
Expliquer les mots "abysse, plaine abysalle, fosse des Mariannes".
Situer cette région sur une carte.
Objectifs : " savoir que la différence de pression au sein d'un liquide
homogène dépend de la différence de profondeur".
"Pratiquer une démarche expérimentale pour établir un modèle à partir d'une série de
mesures".
Variation de pression au sein d'une éprouvette graduée remplie
d'eau d'une hauteur de 50 cm.
La masse volumique de l'eau de mer est constante sur une profondeur de
60 m et est voisine de 1050 kg m-3.
DP =rgh=1050*9,8*60 = 6,1 105
Pa ~6 bar. Le
sous-marin peut encore descendre de 60 m.
|
|
Dans le cadre d'un TPE un groupe d'élèves
trouve un protocole déterminant la poussée d'Archimède à l'aide d'une balance.
Sans
faire appel à la notion de poids apparent et en vous aidant
éventuellement d’un schéma, expliquer en une dizaine de lignes comment cette mesure est
possible.
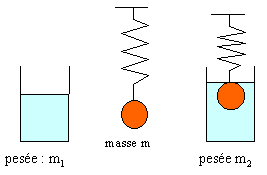
Une balance est un dynamomètre ; ce dispositif affiche une masse.
Pesée d'un bêcher contenant de l'eau : masse m1.
On suspend un solide S de masse m à un ressort de constante de raideur
k. Celui-ci s'allonge d'une longueur x1
à l'équilibre. On plonge le solide S dans le bêcher (masse d'eau
déplacée me ). On observe un nouvel équilibre avec
un nouvel allongement x2 du ressort et une nouvelle lecture de
masse m2.
Tension ressort (N) = raideur
(Nm-1) * allongement (m)
A
l'équilibre la tension du ressort est égale au poids de la masse
accrochée.
Sphère dans l'air (la
poussée de l'air est négligeable) : mg= kx1.
Sphère dans l'eau :
tension = poids réel- poussée.
mg-poussée= kx2 ; kx1-poussée= kx2 ; poussée= k(x1-x2)=
(m1-m2)g.
La mesure du volume de l'objet peut être réalisée par différence de
volume en le plongeant dans une éprouvette graduée contenant de l'eau.
On peut identifier le poids du volume d'eau déplacé à la poussée
d'Archimède.
Préciser
à partir d’arguments accessibles à un élève de lycée laquelle des deux
schématisations (A) ou (B) de la figure (6), illustrant la flottaison
d’un objet de masse volumique inférieure
à celle de l’eau, est correcte.
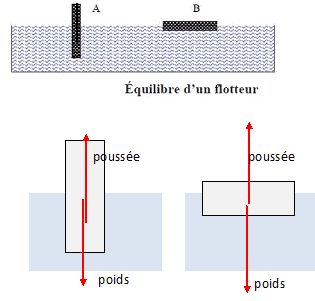
Le flotteur est en équilibre sous l'action de son poids et de la
poussée d'Archimède due à l'eau (la poussée due à l'air est négligeable
rair
<< reau ).
A : le centre de gravité de l'objet est situé au dessus du centre de
poussée ( point d'application de la poussée ). Dans le cas de roulis (
le navire s'incline sur babord ou tribord ), l'objet se renverse :
l'équilibre est instable.
B : le centre de
gravité de l'objet
est situé au dessous du centre de poussée. Dans le cas de roulis ( le
navire s'incline sur babord ou
tribord ), l'objet ne se renverse pas : l'équilibre est stable. (
Utilité de la quille d'un bateau).
« Méfiez-vous de l'oeuf
qui flotte ! »
Un groupe d’élèves de 5ème
souhaite présenter au concours C.Génial Collège une tentative d’explication de la « recette de
grand-mère » énonçant qu’un oeuf périmé flotte alors qu'un oeuf frais coule au fond d’un récipient
rempli d’eau. Le travail est réalisé dans le cadre d’un atelier scientifique.
Proposer
des hypothèses et des expériences afin d’étudier cette affirmation.
L'oeuf s'est mis à flotter : au cours du temps, la coquille de l'oeuf
devient plus poreuse et l'oeuf se déshydrate.
Hypothèse 1
: la masse diminue, le volume reste constant.
Le poids diminue alors que la poussée reste constante : la poussée
l'emporte sur le poids.
Hypothèse 2
: la masse reste constante, le volume croît.
Mesurer tous les
quatre jours la masse et le volume d'un oeuf laissé à l'air libre.
Répéter ces mesures durant quatre semaines.
|
|
|




