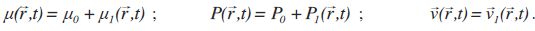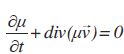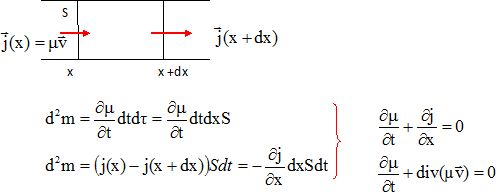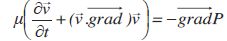La plongée sous marine : ondes
acoustiques en milieu marin, protection thermique
:
Agrégation interne 2014.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
|
|
|
|
|
|
|
Ondes
acoustiques en milieu marin.
L’eau
est considérée ici comme un milieu fluide suffisamment compressible
pour que lui soit associé un coefficient de compressibilité
isentropique cs
défini par : 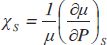 , µ est la masse volumique et P la
pression.
μ
Justifier
l’hypothèse d’une « transformation isentropique » dans le cas de la
propagation d’une onde sonore.
La transformation est réversible : les effets dus à la viscosité sont
négligeables, le milieu marin étant suffisamment élastique et parfait.
La durée caractérisant les phénomènes de diffusion thermique est très
supérieure à la durée caractérisant les variations au cours du temps
des grandeurs étudiées : en conséquence la transformation est
adiabatique.
Une transformation réversible et adiabatique est isentrope.
On considère une onde sonore se propageant dans un milieu fluide. On
néglige les effets de la viscosité et de la pesanteur. En l’absence de
l’onde, la masse volumique du milieu vaut µ 0, la pression
locale P 0, et le fluide est au repos par rapport au
référentiel terrestre supposé galiléen.
Lors du passage de l’onde, le fluide subit une petite perturbation qui
modifie localement la masse volumique, la pression et la vitesse v
d’une particule mésoscopique de façon suivante :
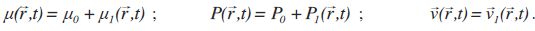
Les grandeurs scalaires ou vectorielles d’indice 1 sont des infiniment
petits du premier ordre.
Rappeler
les hypothèses de « l’approximation acoustique ».
Les équations peuvent être linéarisées :
le fluide en équilibre est perturbé par une onde sonore, mais les
écarts des valeurs de P et µ sont très faibles ( infiniment
petits du premiers ordre ).
On rappelle l’équation locale de la conservation de la masse obtenue en
mécanique des fluides : 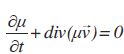 Justifier
en quoi cette équation traduit la conservation de la masse
Justifier
en quoi cette équation traduit la conservation de la masse.
Soit une portion de fluide de section S et de longueur dx, soit j le
vecteur courant, soit dm = µSdx la masse du volume dv = Sdx, soit d 2m
la variation de masse pendant dt, on va établir le bilan entre deux
instants proches t et t+dt :
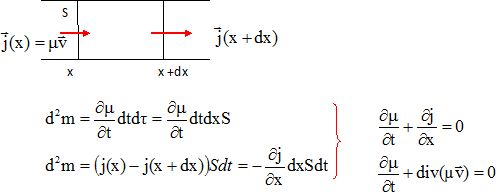
Par analogie avec l’équation locale traduisant la conservation de la
masse, écrire
deux autres équations locales de conservation rencontrées dans d’autres
domaines et préciser pour chacune d’elles sa signification physique.
En électrocinétique et électromagnétisme : la charge se conserve.
Electromagnétisme dans le vide : l'énergie se conserve.
On rappelle l’équation d’Euler obtenue en mécanique des fluides : 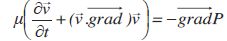 Expliciter
ce que traduit cette équation. Rappeler les hypothèses liées à sa
validité
Expliciter
ce que traduit cette équation. Rappeler les hypothèses liées à sa
validité.
Cette équation exprime la seconde loi de Newton à une portion de fluide.
Le premier terme est l'accélération locale, le second l'accélération
convective et le terme de droite les forces volumiques. Dans le cas de
l'onde acoustique la seule force volumique correspond au gradient de
pression.
En
utilisant l’approximation acoustique, linéariser les deux équations
ci-dessus ainsi que l’expression de cs.
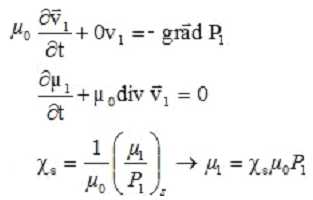 Établir
l’équation aux dérivées partielles vérifiée par la surpression P1
Établir
l’équation aux dérivées partielles vérifiée par la surpression P1.
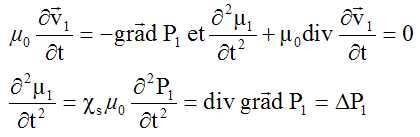 En
déduire l’expression de la célérité c de l’onde en fonction de µ0 et cs
En
déduire l’expression de la célérité c de l’onde en fonction de µ0 et cs.
On identifie csµ 0
à 1/c 2 soit c = ( csµ 0) -½.
Comparer
les valeurs des célérités du son dans l’air ca, et dans l’eau, ce.
Dans l'air : c a = (0,7 10-5 *1,2)-½ =345 ~3,5 102
m/s ;
dans l'eau : ce
= (5,0 10-10 *1,0 103)-½
=1414 ~ 1,4 103 m/s.
|
| .
. |
|
|
Etude
de la
transmission d’un son à travers le dioptre air-eau.
On
considère une onde acoustique sonore, plane de fréquence n se
propageant dans l’air et arrivant perpendiculairement sur un plan d’eau
supposé parfaitement
plan. Chaque milieu, l’air et l’eau, est caractérisé par une impédance
acoustique Z, avec Z =µ0c, µ0 et c étant respectivement
la
masse volumique du milieu au repos et la
célérité du son dans ce milieu. On note avec l’indice « a » les
grandeurs relatives à l’air, et
avec l’indice « e » celles relatives à l’eau.
Les
coefficients de réflexion RPs et de transmission TPs
en puissance
représentent la fraction de puissance sonore réfléchie et transmise à
l’interface de deux
milieux. Leurs expressions en fonction des impédances de chaque milieu Za
et Ze
sont :
Rps = [(Ze-Za) / (Ze+Za)]2
et Tps
= 4ZeZa
/ (Ze+Za)2 .
Conclure
sur la conservation de l’énergie acoustique lors de la
transmission d’une onde acoustique lors de la traversée d’un dioptre «
eau-air ».
Ze =1,0 103 *1,4 103
=1,4 106 kg m2 s-1 ; Za
=1,2 *345 =414 kg m2 s-1 ;
Rps = [(1,4 106-414) / (1,4 106+414)]2 =0,9994.
Tps
= 4*1,4 106 *414 / (1,4 106+414)2 =1,2 10-3.
Seulement 0,1 % de la puissance sonore est transmise à la traversée du
dioptre eau-air.
Donner
la signification de l’expression « adapter les impédances »
et la condition que doivent remplir les impédances respectives des deux
milieux pour qu’il
en soit ainsi.
Pour
une bonne transmission de la puissance à l'interface de 2 milieux, il
faut que les impédances de chaque milieu soit du même ordre de
grandeur. Tps est
alors proche de 1.
Citer un
exemple où cette adaptation est recherchée.
En échographie, un gel est placé sur la peau ; on utilise des
pavillons acoustiques sur les instruments de musique.
On définit l’indice acoustique nac par : nac = ca/ce.
Évaluer
l’indice acoustique nac.
nac = 345 / (1,4 103) =0,25.
Pour
une onde acoustique, expliquer à l’aide d’un schéma si le phénomène de
réflexion totale s’observe pour un sens de propagation allant de l’air
vers l’eau ou de l’eau vers l’air.
L'angle de réfraction est plus petit dans le milieu ou la vitesse est
la plus faible.

Est-il
efficace de rappeler des plongeurs en sifflant ou en agitant une cloche
depuis le pont d’un bateau ? Pourquoi ? Proposer une meilleure méthode.
La
transmission de l'onde sonore est quasiment nul dans le sens
air-eau. Il vaut mieux taper sur la coque sous la ligne de flottaison,
plutôt que d'agiter une cloche.
|
.
|
|
Protection
thermique.
Un plongeur (sans combinaison) dont la température interne est
initialement qp se
déplace dans de l’eau à la température qe supposée
uniforme et constante.
Décrire
en quelques lignes les processus possibles de transfert thermique entre
le corps du plongeur et le milieu environnant.
Par
conduction, transport de proche en proche du corps chaud vers le corps
froid ; par convection ou déplacement, mouvement de matière ; transfert
radiactif : le rayonnement électromagnétique transporte de l'énergie.
Donner
sans calculs, mais en justifiant, la température du plongeur au bout
d’un temps suffisamment long dans le cas où il n’y a aucune source
interne d’énergie.
Sans source interne d'énergie, la
température du corps du plongeur est égale à la température de l'eau au
bout d'un temps suffisamment long ; l'équilibre thermique est atteint.
Pour maintenir sa température interne, le corps humain produit une
puissance thermique Pth supposée
constante. Les échanges entre la surface extérieure de la peau et le
milieu fluide environnant, de température constante et uniforme Te,
sont modélisés par un flux thermique F
p-->e vérifiant une loi de la forme : F p-->e = -K(Te-T), où K est un paramètre
caractéristique, T la température absolue du plongeur, variable, et Te
la température absolue du milieu extérieur.
Justifier
que K s’appelle la « conductance thermique » du système.
Résistance thermique Rth = (T2-T1) / F1-->2 ;
K = F p-->e /(T-Te).
K est l'inverse d'une résistance, c'est donc une conductance.
La conductance
thermique du plongeur sans combinaison est notée Kp.
Établir,
en justifiant toutes les étapes, l’équation différentielle de
l’évolution temporelle de la température T du plongeur supposée
uniforme dans tout son corps.
On introduira cp la capacité thermique massique du plongeur
et mp sa masse.
Pendant l'intervalle de temps dt :
variation de l'énergie interne du plongeur : mpcpdT
;
transfert thermique du corps vers l'eau : -Kp(T-Te)dt
;
énergie produite par le corps humain Pthdt ;
mpcpdT
=Pthdt-Kp(T-Te)dt ;
mpcpdT/dt
+Kp(T-Te)
=Pth.
dT/dt +Kp(T-Te)/ (mpcp) = Pth/(mpcp).
En déduire
l’évolution temporelle T(t) de la température du corps du plongeur.
On pose
A =Kp/ (mpcp) ; T(t)-Te = B
exp(-At) + Pth
/ Kp avec B une constante.
A t = 0, T = Tp : Tp - Te = B+ Pth
/ Kp ; B = Tp - Te- Pth / Kp ;
T(t)-Te =(Tp - Te- Pth / Kp )exp(-At) + Pth / Kp ;
T(t) = Te +(Tp - Te- Pth / Kp )exp(-At) + Pth / Kp.
Exprimer la
constante de temps tth du phénomène et la
calculer. Commenter le résultat.
tth =
1/A = mpcp/Kp =75*4 103
/ 16 ~1,9 104 s~5,2 h, valeur bien supérieure à la durée
d'une plongée.
Montrer que la
température limite Tlim atteinte par le
corps est donnée par : Tlim = Te + Pth
/ Kp.
En régime permanent dT/dt
=0 ; Kp(Tlim-Te)/
(mpcp) = Pth/(mpcp) ; Kp(Tlim-Te)
= Pth.
Dans
les mers tempérées : Tlim =20+120/16 =27,5 °C.
Dans les
mers chaudes : Tlim =28+120/16 =35,5 °C.
Lorsque la température interne du plongeur atteint qhyp= 35°C,
l’hypothermie peut devenir fatale. Le plongeur utilise donc une
combinaison, caractérisée par une conductance Kcomb, qui
modifie la constante Kp en K’.
Justifier,
en s’aidant éventuellement d’une analogie électrique, que K’ est telle
que : 1/K' = 1/Kp + 1/Kcomb.
Le flux thermique sortant du plongeur traverse sa combinaison. Les
résistances thermiques en série s'ajoutent. La conductance est
l'inverse d'une résistance thermique.
L'inverse des conductances s'ajoutent. K' = Kp Kcomb /( Kcomb+ Kp).
Expliquer l’impact
de la combinaison sur la constante de temps tth et la température Tlim.
t'th
= mpcp/K' =mpcp( Kcomb+ Kp)/ (Kp Kcomb ) = tth ( Kcomb+ Kp) / Kcomb = tth ( 1+ Kp / Kcomb.
La constante de temps augmente.
T'lim
= Te + Pth / K' = Te + Pth ( Kcomb+ Kp)/ (Kp Kcomb ). Tlim
croît.
Commenter la
pertinence du port d'une combinaison en eau tropicale, du point de vue
du risque d'hypothermie.
En eau tropicale chaude, le plongeur ne risque par l'hypothermie : la
combinaison n'est pas nécessaire.
Les combinaisons de plongée couramment utilisées pour des températures
d’eau de mer tempérées ou tropicales, sont constituées à base de
néoprène poreux d’épaisseur x (3 mm,
5 mm, ou 7 mm) dont on peut modéliser la conductance Kcomb
par une loi du type : Kcomb = 0,1x-1 W K-1.
Choisir,
en argumentant, parmi les trois valeurs proposées, l'épaisseur minimale
x qui évite l'hypothermie dans une mer tempérée.
Tlim doit rester supérieure à 35°C. T'lim - Te
<35-20 ; T'lim
- Te < 15 °C dans les mers tempérées.
Pth
( Kcomb+
Kp)/ (Kp Kcomb ) <
15 ; Pth
( Kcomb+
Kp) < 15Kp Kcomb.
120 (0,1x-1 +16)
<15 0,1x-1 *16
; 7,5 (0,1x-1 +16) <1,5x-1 ; 120 <( 1,5-0,75 )x-1 ;160 <
x-1
; x > 1/160 ; x >0,00625 m ; x > 6 mm.
Citer une autre
raison pour laquelle il est recommandé de porter une combinaison pour
pratiquer la plongée sous-marine, cela quelle que soit la température
de l'eau.
La combinaison protège le derme.
|
|
|
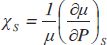 , µ est la masse volumique et P la
pression.
, µ est la masse volumique et P la
pression.