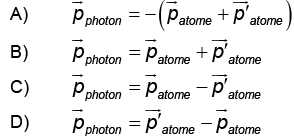Physique
quantique : refroidir des atomes à basse température. Concours
Avenir 2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
La température est liée à l’agitation
thermique de la matière.
Pour refroidir des atomes à très basse température (moins d’un kelvin),
une technique, développée dans les années 80, consiste à diminuer
l’agitation thermique à l’aide d’un laser. En effet quand l’atome
absorbe une photon de fréquence appropriée, ce phénomène s’accompagne
d’un transfert de quantité de mouvement.
Avec h la constante de Planck et c la vitesse de la lumière dans le
vide, la relation entre l’énergie d’un photon et sa fréquence f ou sa
longueur d’onde l
est :
Ephoton =h
l ; Ephoton = hc / f ; Ephoton =h f / c ; Ephoton =h c / l.
( exact ).
La quantité de mouvement du photon, en
fonction de sa longueur d’onde est :
p
= h / l
(exact ) ; p = h l
/ c ; p = h c / l
; p = h l.
Dans
cet expérience, on souhaite refroidir des atomes de rubidium. Pour
cela, on choisit un laser de longueur d’onde l = 780 nm. Pour
se protéger les yeux d’un retour accidentel du faisceau, on doit
utiliser des lunettes colorées, constituant un filtre qui ne laisse
passer que certaines longueurs d’ondes, les plus éloignées possibles de
celle que l’on souhaite bloquer. Ces lunettes de sécurité doivent être
de couleur :
violette
(exact) ; verte ; jaune ;
rouge.
Les
longueurs d'onde du domaine visible, les plus éloignés de 780 nm (
rouge ) sont proches de 400 nm ( couleur violette ).
La quantité de
mouvement de l’atome de masse m se déplaçant à la vitesse v est :
patome = ½m v ; patome = m v (exact
) ; patome
=mv2 ; patome
= ½mv2.
Au cours de
l’absorption d’un photon par un atome, en négligeant la gravitation, la
quantité de mouvement du système {atome + photon} :
diminue ; est
constante ( exact ) ; augmente ; cela dépend de
la situation initiale.
On note patome
la quantité de mouvement initiale de l’atome, et p’atome
cette grandeur après l’absorption du photon. Dans le cas où le photon
et l’atome se dirigent l’un vers l’autre, la relation entre les
quantités de mouvement est :
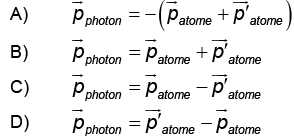
|
| .
. |
|
|
Après l’absorption du
photon (supposée instantanée), l’atome se désexcite spontanément en une
durée moyenne de l’ordre de Dt
= 10-8 s. . Comme la réémission du photon se
fait dans une direction aléatoire, en moyenne la phase de désexcitation
de l’atome ne modifie pas son mouvement, contrairement à la phase
d’absorption.
Au bout de la durée Dt,
l’atome est donc prêt pour un nouveau cycle absorption/désexcitation.
En appliquant le théorème du centre d’inertie (2ème loi de Newton) à
l’atome de masse m, son accélération moyenne en valeur algébrique dans
le référentiel du laboratoire est :
a
= 1/m(p'atome - patome) / Dt. (
exact ).
a = 1/m(patome
- p'atome) / Dt.
a = 1/m(v'atome - vpatome)
/ Dt.
a = 1/m(vatome - v'atome)
/ Dt.
a = Dv / Dt avec Dv = v'-v = p'atome / m -patome / m.
Un atome de rubidium qui absorbe des photons de longueur d’onde 780 nm
est ralenti et subit alors une décélération moyenne de 6×105
m.s-2. Par ailleurs on calcule qu’à température
ambiante, les atomes de rubidium à l’état gazeux sont animés d’une
vitesse d’environ v = 300 m.s-1.
La durée nécessaire pour arrêter les atomes est :
2 10-5 s ; 5 10-4 s
(exact ) ; 2 10-3 s ; 5 10-2
s.
a = Dv / Dt ; Dt =Dv / a
= 300 / (6 105) =5 10-4 s.
Pour
arrêter un atome, les calculs montrent qu’il faut lui faire absorber
environ 50 000 photons. On veut refroidir environ 1 pg de rubidium,
soit 1010 atomes. Le rendement quantique est
estimé à 50 %
(1 photon sur 2 interagit effectivement avec un atome). Les photons
utilisés portent chacun le quantum d’énergie Ephoton
= 2,5×10–19 J.
L’énergie lumineuse fournie par le laser, nécessaire pour arrêter tous
les atomes, doit être au minimum :
2,5
10-4 J (
exact ) ; 2,5 10-2 J ;2,5 J ; 250 J.
1010 *50 000*2,5 10-19 / 0,5 =2,5 10-4 J.
Le laser utilisé fournit une puissance lumineuse de 0,5 W. Sachant que
son rendement est faible : h~
1 %, la puissance perdue sous forme de chaleur est :
4,95 W ; 49,5
W ( exact ) ; 50 W ; 499 W.
Puissance
totale du laser : 0,5 / 0,01 ~ 50 W. Puissance perdue sous
forme de chaleur 50-0,5 = 49,5 W.
Les très basses températures obtenues permettent de réaliser des
horloges atomiques dont l’erreur relative est de l’ordre de 10-13.
Cela signifie qu’en une année, elles se décalent d’environ :
1 s ; 1 ms ; 1
µs ( exact ) ; 1 ns.
1 an =
365*24*3600 s =3,15 107 s ; décalage :3,15
107 * 10-13 ~3 10-6 s = 3 µs.
|
.
|
|
Pour
identifier une molécule complexe, on peut utiliser un certain nombre de
procédés physiques. L’un d’eux consiste à étudier le spectre
d’absorption de la molécule dans l’infrarouge. Les raies correspondent,
dans ce domaine spectral particulier, à des niveaux de vibration des
atomes à l’intérieur de la molécule.
On s’intéresse plus
particulièrement à la liaison covalente entre un atome de carbone et un
atome d’oxygène. On la modélise comme un ressort de raideur k reliant
les deux atomes. On pourra considérer qu’une des extrémités du ressort
est fixe et que l’autre est fixée à une masse m = 1×10-26
kg, libre d’osciller rectilignement sans frottement dans la direction
du ressort.
On identifie sur le
spectre d’absorption la raie correspondante : elle a pour fréquence f =
5×1013 Hz, ce qui correspond à la fréquence des
oscillations du ressort.
La raideur du ressort est k = 1×103 N.m-1
et l’élongation maximale (distance maximale de la masse par rapport à
sa position d’équilibre) est DLmax
= 8×10-12 m.
D’après la loi de Hooke, la force de rappel qui s’exerce sur un ressort
de raideur k,
lorsque la masse est écartée d’une distance DL de sa position
d’équilibre, est :
F
= k DL ; (
exact ) ; F = k DL2
; F = ½k DL2
; F = k / DL.
On
étudie la demi-oscillation qui correspond au passage du ressort, de son
état de compression maximale à son état d’élongation maximale. Le
travail de la force F sur cet intervalle est :
W= F / (2DL)
Faux, formule
non homogène, un travail est une force fois un déplacement.
W = -2F DL.
Faux la
force de rappel n'est pas constante.
W = +2F DL. Faux la force de rappel n'est
pas constante.
Aucun des résultats précédents ne convient. ( exact ).
Quand le ressort est dans son état d’élongation maximale, l’énergie
mécanique du système est Eméca = 3×10-20
J (correspondant ici à l’énergie d’un photon infrarouge absorbé). Une
demi-oscillation plus tard, quand le ressort est dans son état de
compression maximale, l’énergie potentielle du système est alors :
Epot = -3 10-20 J ; Epot
= -1,5 10-20 J ; Epot
= 1,5 10-20 J ; Epot = 3 10-20 J. (
exact ).
Lorsque
le ressort est dans l'état de compression maximale, l'énergie
mécanique
est sous forme potentielle élastique, l'énergie cinétique étant nulle.
L'énergie mécanique de cet oscillateur se conserve.
|
|
|