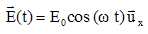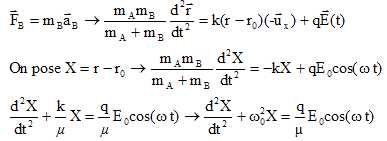Molécule de monoxyde de carbone. Concours CPR 2013 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . La pollution de l'air est un souci croissant qui devient crutial dans les sites sensibles où les concentrations en monoxyde de carbone ( CO) par exemple doivent faire l'objet de mesures constantes et précises. Pour ces mesures, on peut s'interesser au pic d'absorption de CO pour la longueur d'onde l = 4,70 µm. On cherche à comprendre l'origine de cette absorption. Dans quel domaine se situe cette longueur d'onde ? 4,70 µm appartient au proche infrarouge. Calculer la fréquence correspondant à cette longueur d'onde. f = c / l = 3,00 108 / (4,70 10-6) =6,38 1013 Hz = 63830 GHz. On modélise la molécule AB par l'association de deux points matériels A de masse mA et B de masse mB. On étudie cette molécule en se plaçant dans le référentiel barycentrique de la molécule ( noté R*) et associé au référentiel du laboratoire R0. La molécule est supposée rigide ( la distance AB = r est supposée constante ). On étudie ici la rotation de cette molécule autour d'un axe fixe D0 passant par G, barycentre des deux points, perpendiculaire à AB. La molécule tourne à la vitesse angulaire w. On pose GA = rA* et GB = rB*. 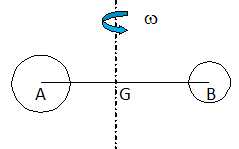Donner l'expression de l'énergie cinétique barycentrique de la molécule. Ec = ½mA vA2 +½mBvB2. vA = w rA* et vB = w rB*. Ec = ½(mA rA*2 +mB rB*2)w2. On écrit Ec = ½Iw2avec I = mA rA*2 +mB rB*2. AN : r = 0,115 nm ; mA =0,016 / NA =0,016 / (6,02 1023) =2,658 10-26 kg ;  mB = 0,012 / NA =0,012 / (6,02 1023) =1,993 10-26 kg ; rA*+rB* = r ; mA rA* = mB rB*; rA*(1+ mA / mB) = r ;  rA*=0,115 /(1+2,658 / 1,993) =0,0493 nm ; rB*=0,0657 nm. I =(2,658* 0,04932+1,993 *0,06572 ) 10-26 10-18=1,51 10-46 kg m-2. On montre que l'énergie liée à la rotation d'une molécule est quantifiée par un nombre quantique J selon la relation : Er =J(J+1) h2 /(8p2I), où J est un nombre entier naturel. Calculer la valeur de la fréquence de la raie spectrale correspondante à la transition entre les deux niveaux d'énergie ( de rotation) J=0 et J=1. f = DE / h avec DE = h2 /(8p2I) ; f = h /(8p2I) . f = 6,63 10-34/(8*3,142*1,51 10-46)=5,56 1010 Hz=55,6 GHz. Même quastion pour la transition J=0 et J=2. f = DE / h avec DE = 5h2 /(8p2I) ; f = 5 h /(8p2I) . f =5*5,56 1010 Hz=2,78 1011 Hz=278 GHz. La rotation moléculaire ne permet pas d'expliquer la raie d'absorption à 4,70 µm. . . On modélise la vibration d'élongation le long de la liaison AB par l'association de deux points matériels A(mA) et B(mB) reliés par un ressort de constante de raideur k et de longueur à vide r0 ( on néglige toute autre interaction ). On note r(t) la distance AB. A l'équilibre, la distance est notée re. L'axe orienté de A vers B est noté x'x et a pour vecteur unitaire ux. Le référentiel du laboratoire R0 est galiléen. Le référentiel barycentrique en translation par rapport à R0 est également galiléen. 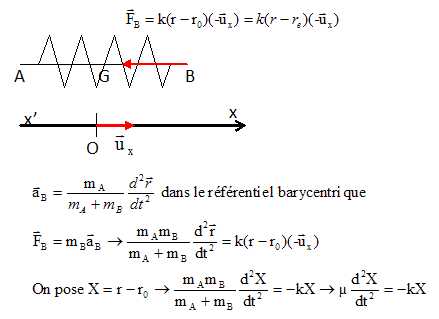A t=0, les vitesses initiales des deux points matériels sont nulles et r(t=0) = rM. Solution générale de l'équation différentielle  : X(t) = Cste  cos (w0t + F) avec w02 = k / µ. X'= -Cste w0 sin (w0t + F) ; X(t=0) = 0  d'où F=0. X(t=0) =Cste = rM -r0 ; X(t) =( rM-r0)cos (w0t). r(t) = r0 +X(t) = r0 +( rM-r0)cos (w0t). Calculer k si f = 6,38 1013 Hz. w0 = 2pf =(k/µ)½ ; k = (2pf)2 µ. k =(2*3,14 *6,38 1013)2( 0,016*0,012/((0,016+0,012) *6,02 1023) =1,83 103 N m-1. . On suppose que l'atome A porte une charge -q et l'atome B une charge +q. On suppose que l'interaction électrostatique entre les atomes est déja prise en compte dans la force de rappel du ressort.. 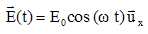On envoie alors sur la molécule alignée suivant l'axe x'x dans la direction de ux, une onde électromagnétique de pulsation w de telle façon que les atomes soient  chacun soumis au champ électrique Sous l'effet de l'onde les atomes se déplacent suivant l'axe x'x. Donner l'équation différentielle vérifiée par X. 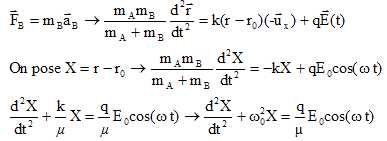En utilisant la méthode des nombres complexes, déterminer l'amplitude maximale des oscilations Xmax. X= Xmax ejF ; X" = -w2X =-w2Xmax ejF. L'équation différentielle s'écrit alors :-w2Xmax ejF+w02Xmax ejF =q/µE0. Xmax ejF( w02-w2) =q/µE0. On identifie Xmax =q/(µ( w02-w2))E0. Pour w = w0, on observe un phénomène de résonance.

menu