Quantité de
mouvement, mouvement parabolique, déviation d'ion, mouvement
circulaire. Concours Puissance 11 ( Fesic )
2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
Choc et
quantité de mouvement.
Un wagon de masse mw= 30 t, immobile sur une voie ferrée
rectiligne, est percuté par une locomotive de masse mL=: 120
t se déplaçant en marche arrière à une vitesse vL=1,8 km.h-1.
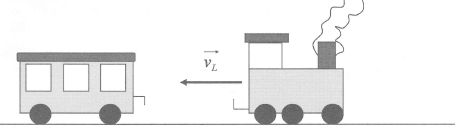
Le système {locomotive + wagon} est supposé isolé et l'étude est
réalisée dans le référentiel terrestre
considéré comme galiléen.
a) Il y a
conservation de la masse du système {locomotive + wagon}, mais pas de
sa quantité de
mouvement. Faux.
Le vecteur quantité de
mouvement du
système se
conserve lors du choc.
b) Avant le choc
avec le wagon, la quantité de mouvement de la locomotive est pL=
60 kg.m.s-1. Faux.
mL vL
= 120 103 *1,8 / 3,6 =6,0 104
kg m s-1.
Deux situations peuvent se produire
-1ère situation : Lors du choc , le wagon s'accroche à la
locomotive.
c) La vitesse de
l'ensemble ( locomotive + wagon) après accrochage est V= 1,44 km.h-1.
Vrai.
Conservation
de la quantité de mouvement : 6,0 104
= (mw+mL)V = (30+120) 103
V ;
V =6/15 =0,4 m/s ou
0,4*3,6 = 1,44
km.h-1.
- 2ème situation :
Lors du choc, le wagon et la locomotive restent séparés. Après le choc,
la locomotive a
une vitesse de 1,08 km.h-1.
d) Après le choc,
le wagon a une vitesse de 0,80 m.s-1. Faux.
Conservation
de la quantité de mouvement : 6,0 104
= mwv +120 103 *1,08/3,6 ;
6,0 104 = 20 103 v
+3,6 104 ; v =
24/20 = 1,2 m/s.
|
|
|
Le passing shot.
Le passing shot consiste pour un joueur de tennis (joueur A) à envoyer
la balle le long de la ligne de coté et au fond du court, lorsque le
joueur adverse (joueur B) monte au filet. Les dimensions du court sont
données sur le schéma suivant (échelle et proportions non respectées) :
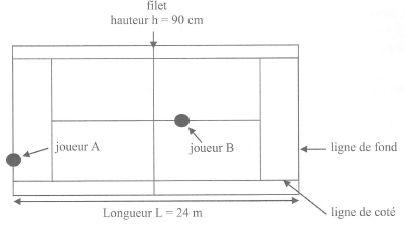
Lejoueur A tente un passingshot. A t0=0 s, placé sur sa
ligne de fond, il frappe la balle à une hauteur z0=50 cm,
selon un angle a=: 10° par
rapport au plan horizontal. Pour simplifier, on considérera que le
mouvement se fait sans frottements et on négligera la poussée
d'Archimède : le mouvement est parabolique et se fait dans un plan
vertical parallèle à la ligne de coté. La vitesse initiale de la balle
est v0= 25 m.s-l.
L'étude est réalisée à l'aide d'un repère cartésien d'axes Ox et Oz et
on suppose que le joueur B n'a pas réussi à toucher la balle.

a). Les équations
horaires de la balle sont :
x(t) =v0.(cos a) t
; z(t) =½gt2+ v0.(sin a)
t + z0. Faux.
x(t) =v0.(cos a) t ; z(t) =-½gt2+
v0.(sin a) t + z0.
b) L'équation de la
trajectoire est z = -gx2/(2(v0cos a)2)+ x tan a + z0. Vrai.
c) La balle passe à
1,4 m au-dessus du filet. Vrai.
z = -10*122/(2(25cos
10)2)+
12 tan 10 + 0,50
= -1,2 +2,1 +0,50 =1,4 m.
d) La balle
retombe plus loin que la ligne de fond du joueur B. Faux.
z = -10*242/(2(25cos 10)2)+ 24 tan 10 + 0,50 = -4*1,2 +2*2,1 +0,50 =
-4,8 + 4,2+0,5 = -0,1 m.
|
.
|
|
Déviation
d'atomes d'hélium.
Afin de mesurer la masse m d'un atome d'hélium 42He
, on étudie la déviation d'un jet d'hélium ionisé passant dans une
chambre où règne un champ électrostatique uniforme. Les atomes d'hélium
ionisés
pénètrent sous forme d'ions He2+ dans le dispositif, avec
une vitesse initiale horizontale de valeur v0= 1,0 x 10+6
ms-1, et sont recueillis surun détecteur situé à une
distance D= 10 cm de l'ouverture. Le champ électrostatique a une valeur
E=10 kV.m-1. On négligera toutes les forces autres que la
force électrique qui s'exerce sur chaque ion. On observe une déviation
vers le bas de d= 2,4 x 10-3 m.
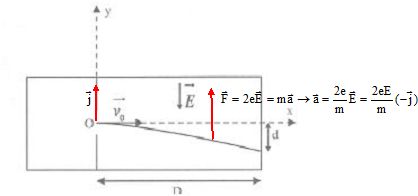
Donnée : charge élémentaire e = 1,6 10-19 C.
a) Les équations
horaires d'un ion hélium sont : x(t) =v0t et y(t) = -eE/m t2.
Vrai.
b) La trajectoire des ions est
hyperbolique. Faux.
Trajectoire parabolique y
= -eE/(mv02) x2.
c) La masse d'un
ion He2+ est d'environ m =6,7 x 10-27 kg. Vrai.
m= -eED2/ (-dv02)= 1,6 10-19*104*10-2
/(2,4 10-3* 1012)=1,6 / 2,4 10-26 =6,7
10-27 kg.
d) L'isotope 32He ionisé sera plus
dévié par ce dispositif.
Vrai.
La masse de cet isotope est plus petite et
y = -eE/(mv02) D2.
|
|
|
Cinématique des
mouvements circulaires.
Galatée est le quatrième satellite naturel de Neptune. Il a été
découvert lors du passage de la sonde Voyager 2 en 1989 (désignation
temporaire S/1989 N 4). Son nom vient de Galatée, une néréide (nymphe
marine) de la mythologie grecque' D',après wikipedia.
L'orbite de Galatée (point G) est quasi circulaire. On se place dans le
réferentiel Neptunocentrique affecté d'un repère de Frénet.
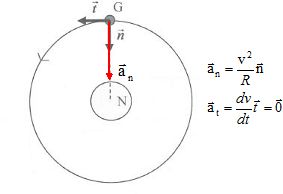
Données : Rayon de l'orbite
de Galatée : R= 6,2 x 104 km ; période de révolution de
Galatée : T=3,7 104 s ;
Masse de Neptune : M=1,0 x 1026 kg ; Constante
gravitationnelle : G =6,7 x 10-11 S.I.
a) Le mouvement de
Galaté est uniforme. Vrai.
b) Dans le repère de Frénet, on a : Faux. Faux.
c) La vitesse de
Galatée est donnée par : v= (GM/R)½ et a pour valeur 1,0 x 104
m.s-1. Vrai.
v=
(6,7 10-11*1026/(6,2 107)½
=(6,7 / 6,2 108)½ ~1,0 x 104
m.s-1.
d) La période de révolution de
Galatée T = 2p ( R3/(GM))½.
Vrai.
La troisième loi de Kepler s'écrit
: T2 = 4p2/(GM)
R3.
|
|
|