Loi
de l'hydrostatique appliquée à la plongée,
concours général 2013.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
La
plongée sous-marine est une activité qui peut se pratiquer à différents
niveaux : activité professionnelle
pour certains pêcheurs, sport extrême ou encore passe-temps et
découverte d’un milieu naturel. Nous allons au cours de ce sujet
aborder différents problèmes physiques nécessaires à une bonne
compréhension et à une pratique en toute s´ecurité de ce sport. La
plongée en apnée consiste à s´ejourner sous l’eau en retenant son
souffle. La durée de l’apnée dépend des caractéristiques
morphologiques du plongeur, mais aussi de facteurs extérieurs qui
augmentent la consommation d’oxygène.
Citer
trois facteurs qui peuvent modifier la durée de l’apnée.
La durée de l'apnée dépend du volume d'air dans les poumons, de l'état
du plongeur ( activité musculaire, repos, stress ) du plongeur, de la
température de l'eau.
Les
lois de l’hydrostatique.
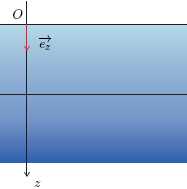
On s’intéeresse dans cette partie à l’évolution de la pression en
fonction de la profondeur. On repère la surface de l’eau par son
ordonnée z = 0. L’axe est orienté vers le bas. On suppose que le
champ de pesanteur g est uniforme.La
pression dans un fluide de masse volumique r vérifie la
relation de la statique de fluides : dP/dz = rg.
Donner la
valeur de la masse volumique re
de l’eau sous pression atmospérique P0 (c’est
à dire pour z = 0).
re
= 1,0 103 kg m-3 ou 1,0 g
cm-3.
On suppose que l’eau est un liquide homogène et incompressible en
équilibre dans le champ de pesanteur g = 9,81 m· s−2.
La masse volumique de l’eau est donc supposée constante et égale à re.
Montrer
que la pression évolue avec la cote z selon la loi suivante
: P = P0 + regz
(2)
dP = re g
dz ; intégrer : P = re
g z
+ cste.
P(0)= P0 = Cste ; P = P0
+ reg z
.
P0 est la
pression atmosphériqueet z la cote du point considéré.
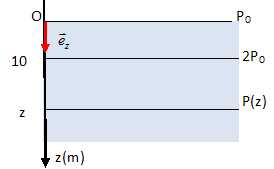
Représenter
sur une figure similaire à la figure ci dessus les isobares suivantes
: P = P0, P = 2P0 et P(z).
Composition
de l’air et ´equation d’état.
La durée de l’apnée d´epend de la capacité de chaque pratiquant à
économiser l’oxygène contenu dans son organisme et ses poumons. En
dehors des capacités génétiques et de l’état de forme du sujet,
certains facteurs peuvent accentuer cette consommation d’oxygène. Il
est alors important de comprendre le comportement de l’air inspiré en
fonction de la profondeur. Nous allons, dans un premier temps et pour
décrire certains phénomènes physiques assimiler l’air à un gaz
parfait : PV = nRT
où P est la pression, V le volume, n la quantité de matière en mol, R
la constante des gaz parfaits
R = 8, 31 J ·K−1 ·mol−1,
et T la température en kelvin (K). On définit la température en kelvin
de la manière suivante :
T(K) = 273 + q(
◦C).
Rappeler
les unités dans le système international de la pression P et du volume V.
La pression s'exprime en pascal ( Pa) et le volume en m3.
On suppose que l’air que l’on inspire est constitué de 79% de diazote
et de 21% de dioxygène.
Citer
deux autres gaz présents dans l’air sous forme de trace.
Les gaz nobles , dioxyde de carbone, vapeur d'eau, méthane, ozone.
Dans la suite, on négligera la présence des gaz autres que le
diazote et le dioxygène.
Calculer
la masse molaire de l’air.
M= M(N2)*0,79 +M(O2)*0,21
=28*0,79 +32*0,21 =22,12 +6,72 =28,84 ~28,8 g/mol.
L’air étant à la température T0 = 288 K et à la
pression P0 = 1, 00.105
Pa, exprimer
puis calculer le volume molaire de l’air, noté Vm0.
Vm0 =RT0/P0
=8,31*288/(1,00 105) =0,0239 m3/mol
= 23,9 L/mol.
Toujours dans ces conditions, exprimer
puis calculer la masse volumique de l’air. En déduire la masse d’air
contenu dans un volume V = 1 L
rair
=M/Vm0 =28,84 10-3 /
0,0239 =1,205 ~1,21 kg m-3 où 1,21 g/L.
|
| ..
.. |
|
|
La pression
partielle d’un gaz dans un mélange de volume VT
est égale à la pression de ce gaz s’il occupait à lui seul le volume
total VT.
Exprimer
les pressions partielles de dioxygène PO2 et de
diazote PN2 en
fonction de P0. Calculer
PO2 et PN2 en bar.
PO2 = 0,21P0 =0,21 105
Pa ; PN2
= 0,79P0 =0,79 105 Pa.
Pour
étudier les effets de l’apnée sur nos poumons, des scientifiques ont
réalisé différentes expériences au début du vingtième siècle. L’une de
ces expériences a été menée grâaceà un bathyscaphe.
Un bathyscaphe
est un sous-marin conçu pour se déplacer principalement verticalement.
Un ballon aux parois souples contenant le volume V0
= 1 L d’air à la pression atmosphérique (P0 = 1,
00.105 Pa) est attaché à un
sous-marin initialement à la surface de l’eau. Des mesures ont
permis de relever l’évolution du volume, et de la densité de l’air
contenu dans le ballon lors de la descente du sous-marin en fonction de
la profondeur z.
Dans la suite de
cette question, l’air est assimilé à un gaz parfait et l’eau à un
fluide incompressible. La température de
l’océan est supposée homogène et égale à q0
= 15°C.
Calculer
la quantité de matière nb et la
masse mb d’air
contenu dans le ballon.
nb=V0 /Vm0=1
/23,9 =4,184 10-2 ~4,2 10-2
mol ; mb ~1,2 g.
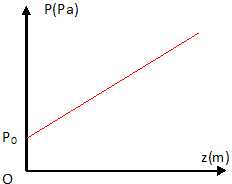
Représenter
en fonction de z l’évolution de la pression au sein du ballon.
Exprimer
le volume Vb du ballon
en fonction de z.
Vb = nbRT/P =nbRT/(P0
+ regz ).
Calculer
le volume occupé par l’air de ce ballon dans la fosse des
Mariannes située à une profondeur z =11000 m. Calculer r la masse
volumique de l’air à une telle profondeur. Comparer à la masse
volumique de l’eau.
En supposant la température et g constantes à cette profondeur : P
=1000 *9,81*11000 + 1,00 105 =1,08 108
Pa.
Vb =4,184 10-2*8,31*288 /
(1,08 108) ~9,3 10-7
L.
r
=mb
/Vb=1,2 10-3
/ (9,3 10-7) ~1,3 103
kg m-3,supérieure à celle de l'eau.
On
imagine qu’à cette profondeur, la ballon se perce. Que
devrait-on observer ?
La masse volumique de l'air étant supérieure à clle de l'eau, les
bulles d'air devraient couler.
On réalise l’expérience et on observe que
des bulles d’air remontent à la surface. Quelle est
l’hypothèse à remettre en cause ?
La température et
g ne sont pas constantes à cette profondeur. L'air ne peut plus être
considéré comme un gaz parfait.
|
.
|
|
Les scientifiques
ont réalisé différentes mesures lors de la descente. Ils se sont
intéressés au rapport a=
PVm / (RT0) où Vm
représente le volume molaire et où la température est constante et
égale `a 15 ◦C :
| P(bar) |
1,00 |
100 |
150 |
200 |
250 |
300 |
350 |
400 |
500 |
600 |
700 |
| a |
0,945 |
0,981 |
0,997 |
1,025 |
1,064 |
1,109 |
1,157 |
1,212 |
1,333 |
1,452 |
1,575 |
| rair(kg
m-3) |
1,27 |
122 |
180 |
234 |
282 |
325 |
363 |
396 |
450 |
496 |
533 |
Exprimer
la masse volumique rair
de l’air contenu dans le ballon en fonction d’abord du volume molaire Vm et de la
masse molaire Mair de l’air.
En déduire l’expression de la masse volumique rair en
fonction de la
pression P, du coefficient a, de la
température T0, de la
masse molaire Mair et de la
constante des gaz parfaits R.
rair
= Mair / Vm =Mair P /(a RT0 )
=0,0288/(8,31*288) P/a
=1,20 10-5 P/a.
La mesure
du coefficient a
la pression P = 1 bar est-elle conforme à la valeur attendue ? En quoi
est-ce surprenant ?
a= P0Vm
/ (RT0) =1,00 105*0,0239/(8,31*288)~1
dans le modèle des gaz parfaits.
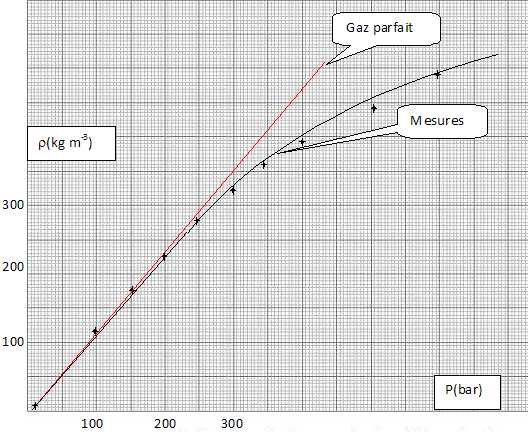
Représenter
la courbe repésentant la masse volumique en fonction de la pression.
Représenter la courbe obtenue en appliquant le modèle du gaz parfait.
Conclure.
Donner
un ordre de grandeur de la pression maximale permettant de travailler
dans l’hypothèse des gaz parfaits. Exprimer la profondeur
correspondante. Est-ce restrictif ?
Jusqu'à une pression de 200 bars ( profondeur : 2000 m), les deux
courbes sont pratiquement confondues. Les plongées en apnée
n'atteignent pas de telles profondeurs.
|
Dans
la suite de l’épreuve, la profondeur maximale permettra de travailler
en considérant que l’air se comporte comme un gaz parfait.
La plongée avec bouteille permet une plus grande liberté d’action du
plongeur dans l’eau que l’apnée.
Désormais, nous allons nous intéresser à la plongée avec bouteille.
On appelle capacité pulmonaire le volume d’air pouvant être inspiré.
Dans la suite, nous allons assimiler cette capacité pulmonaire au
volume Vp des poumons. Nous supposons que le
plongeur est en équilibre
avec le milieu extérieur : en particulier la pression de l’air `a
l’intérieur des poumons est supposée égale à la pression extérieure. On
note VpM le volume maximal des poumons, et Vpm
le volume minimal.
On donne VpM = 5 L et Vpm
= 1 L.
On suppose que le plongeur est à la profondeur z1
= 20 m. L’air de ses poumons occupe le volume Vp1
= 3 L (assimilé au volume de ses poumons). Le plongeur bloque sa
respiration et en particulier n’expire pas. En reprenant la relation
(2), exprimer le volume Vp(z) des poumons du
plongeur à la profondeur z en fonction de z, z1,
Vp1, re,
g et P0.
P = P0 + reg z ; P1 = P0 + reg z1 ; P Vp(z)= nRT ; n = Vp1P1/(RT) =Vp1(P0 + reg z1 )/(RT)
Vp(z)= Vp1(P0 + reg z1 ) /(P0 + reg z ) =Vp1P1/(P1 + reg (z-z1) ).
Quel est le risque encouru par un plongeur qui se déplace verticalement ?
En remontant respiration bloquée, z diminue, le volume des poumons augmente, pouvant dépasé VpM.
En descendant respiration bloquée, z aumentee, le volume des poumons diminue, pouvant dépasé Vpm. Il en résultera des lésions graves des poumons.
Exprimer puis calculer les profondeurs limites
au-del`a desquelles il peut subir des
l´esions (sa respiration ´etant toujours bloqu´ee). Conclure sur le
comportement `a adopter lors de la remont´ee
`a la surface.
|
|
|