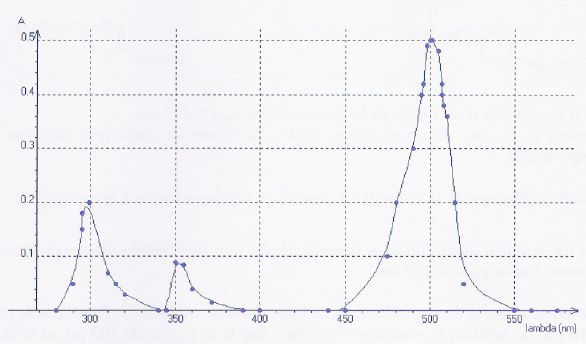
Principe de l'absorption vibrationnelle. Concours général 2014 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Principe de l'absorption vibrationnelle. Cette spectroscopie est une spectroscopie d'absorption. Citer un exemple de spectre mettant en évidence le phénomène d'absorption. Spectre d'absorption de l'éosine : le maximum d'absorption se situe à 500 nm ( couleur cyan). La solution d'éosine a la couleur complémentaire du cyan soit l'orange rosé. La lumière visible est constituée de radiations ou ondes électromagnétiques perceptibles par l'oeil. Rappeler le domaine des longueurs d'onde dans le vide correspondant à la lumière visible. [ 400 nm ; 800 nm ] Le domaine infrarouge utilisé en spectroscopie correspond à des ondes de longueur d'onde dans le vide comprises entre 2,5 et 15 µm.. Donner la relation entre la longueur d'onde dans le vide d'une onde électromagnétique et l'énergie du photon qui lui est associé. E = h c / l. E en joule; c =3,00 108 m/s ; h = 6,63 10-34 J s ( constante de Plank) et l, longueur d'onde en mètre. En déduire l'intervalle d'énergie correspondant au domaine des ondes infrarouges. On exprimera les énergies en joule et en eV. E = 6,63 10-34 *3,00 108 /(2,5 10-6)= 7,96 10-20 J ou 7,96 10-20/(1,6 10-19) =0,497 eV. E = 6,63 10-34 *3,00 108 /(15 10-6)= 1,33 10-20 J ou 1,33 10-20/(1,6 10-19) =8,29 10-2 eV. L'énergie d'une molécule est la somme de quatre termes correspondant à : - l'énergie électronique Ee de la molécule, - l'énergie de vibration Ev due aux oscillations effectuées par les noyaux autour de leur position d'équilibre, - l'énergie de rotation Er de la molécule autour de son centre de masse, - l'énergie de transition Et de la molécule. Les énergies électroniques, de vibration, de rotation sont quantifiées. Donner une définition de ce terme. L'énergie ne peut prendre qu'un petit nombre de valeurs. Toutes les valeurs ne sont pas permises. La différence d'énergie DEe entre deux niveaux électroniques est typiquement de 10 eV,  celle entre deux niveaux de vibration DEv de 0,10 eV et celle entre deux niveaux de rotation DEr de 10-3 eV. Montrer que la spectroscopie infrarouge est une spectroscopie d'absorption vibrationnelle. Les longueurs d'onde utilisées vont de 2,5 µm à 15 µm ; les énergies des photons associés s'étendent de 8 10-2 eV à 0,5 eV. Ces valeurs correspondent à des transitions entre deux niveaux vibrationnels. .. . Pour illustrer cette énergie de vibration on suppose l'analogie entre la liaison chimique et un  oscillateur harmonique linéaire. On se propose d'abord d'étudier un oscillateur élastique, puis d'appliquer cette étude à une molécule diatomique. 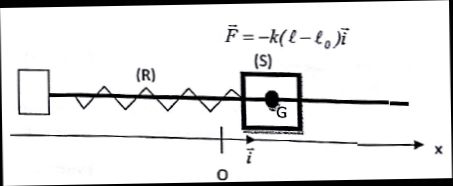Un solide S de masse m, de centre d'inertie G, peut glisser sans frottement sur un axe horizontal. Il est accrocher à un ressort R à spires non jointives, de raideur k = 4,0 N /m et de longueur à vide L0, dont l'autre extrémité est fixe. L'ensemble constitue un oscillateur élastique horizontal, non amorti. La masse du ressort est négligeable devant m, et S entoure l'axe de telle sorte que G se trouve sur celui-ci. On note O l'abscisse de G lorsque S est à l'équilibre. La force de rappel d'un ressort s'écrit : . On étudie le mouvement de translation de S dans le référentiel terrestre supposé galiléen. Le solide est écarté de 10 cm de sa position d'équilibre et abandonné sans vitesse initiale à la date t=0. Représenter, sans souci d'échelle, les forces en G s'exerçant sur le solide S. 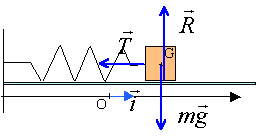En appliquant la deuxième loi de Newton au solide S, montrer que l'équation différentielle régissant le mouvement de son centre d'inertie s'écrit : d2x/dt2 +k/mx=0. Sur l'axe Ox, la somme vectorielle des forces s'écrit : -k(L-L0) = m a. On pose L-L0 = x ; a = d2x/dt2 ; par suite : d2x/dt2 +k/mx=0. Une solution de l'équation différentielle peut s'écrire sous la forme x(t) = Xm cos (2pt/T0+F), où Xm est l'amplitude et F la phase initiale. Retrouver l'expression de la période T0 en fonction de m et k. x' = -Xm 2p/T0 sin (2pt/T0+F) ; x" = -Xm (2p/T0 )2cos (2pt/T0+F) =-(2p/T0 )2 x. Repport dans l'équation différentielle : -(2p/T0 )2 x +k/m x = 0. (2p/T0 )2 = k/m ; T0 =2p(m/k)½. Calculer les valeurs de Xm et de F. x(0) =Xm cos F  = 0,10 ; F  =0 et Xm = 0,10 m. On s'intéresse maintenant aux vibrations d'une molécule diatomique hétéronucléaire. Pour modéliser ces vibrations, on considère que chaque atome se déplace dans un mouvement harmonique. La liaison est représentée par un ressort sans masse de raideur k qui relie les deux atomes 1 et 2 de la molécule. On note Ox l'axe parallèle à la liaison, x1(t) représente à l'instant t la position de l'atome 1 de masse m1, et x2(t) représente celle de l'atome 2 de masse m2. 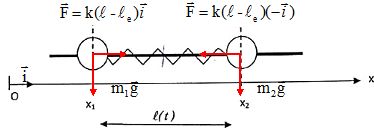On note l(t) la distance entre les atomes à l'instant t et le la distance à l'équilibre. Faire le bilan des forces s'exerçant sur l'atome 1 puis sur l'atome 2. Chaque atome est soumis à une force de rappel et à son poids. En appliquant la seconde loi de Newton à l'atome 1, établir l'équation différentielle du mouvement liant x"1 à l(t). Sur un axe horizontal la seconde loi de Newton s'écrit : k(l-le) = m1x"1. En appliquant la seconde loi de Newton à l'atome 2, établir l'équation différentielle du mouvement liant x"2 à l(t). Sur un axe horizontal la seconde loi de Newton s'écrit : -k(l-le) = m2x"2. Exprimer l(t) en fonction de x1(t) et x2(t) ; en déduire une relation entre leurs dérivées secondes respectives. l(t) =x2(t) -x1(t) ; l"(t) =x"2(t) -x"1(t). En déduire que le mouvement vibratoire peut être décrit par l'équation : µ l"(t)=-k(l-le) , où l'on introduit la masse réduite µ = m1m2/(m1+m2). l"(t) =-k(l-le) / m2-k(l-le) / m1 ; l"(t) =-k(l-le)( 1/m1+1/m2). l"(t) =-k(l-le) (m1+m2 ) / (m1 m2) =-k(l-le) /µ. Par analogie, donner l'expression de la période Tvib et de la fréquence de vibration fvib du système en fonction de µ et k. Tvib =2p(µ/k)½ ; fvib = 1/Tvib = 1/(2p)(k/µ)½. En spectroscopie moléculaire on introduit le nombre d'onde s = 1/l où l est la longueur d'onde dans le vide d'une onde électromagnétique de fréquence f. Les nombre d'onde s'expriment en cm-1. Montrer qu'il existe une relation de proportionnalité entre s et f. l = c / f ; f = c/l = c s. A quelle fréquence exprimée en hertz correspond un nombre d'onde de 1 cm-1 ? 1 cm-1 = 100 m-1 ; f = 3 108 *100 = 3 1010 Hz. Les nombre d'onde de vibration des molécules Br-Rb et Kr-Rb sont respectivement 181 cm-1 et 13 cm-1. La différence des valeurs entre ces deux nombre d'onde peut-elle se justifier par la différence entre les masses du brome et du krypton ? Justifier. Que peut-on en déduire sur les valeurs des constantes de raideur de ces deux liaisons. M(Br) = 80 g/mol ; M(Kr) = 84 g/mol ; M(Rb) = 85 g/mol. m(Br) =0,080 / (6,02 1023) =1,33 10-25 kg ; m(Rb) =0,085 / (6,02 1023) =1,41 10-25 kg. µ(Br-Rb) =1,33 10-25 *1,41 10-25 /((1,33+1,41) 10-25)=6,84 10-26 kg. m(Kr) =0,084 / (6,02 1023) =1,395 10-25 kg. µ(Kr-Rb) =1,33 10-25 *1,395 10-25 /((1,33+1,395) 10-25)=6,81 10-26 kg Les masses réduites étant du même ordre de grandeur, la différence des valeurs des nombres d'onde estt dues à des liaisons de constante de raideur très différentes. Le nombre d'onde  est proportionnel à la fréquence ; la fréquence est  proportionnelle à la  racine carrée de la constante de raideur. A un grand nombre d'onde correspond une plus grande constante de raideur. La constante de raideur de la liaison Br-Rb est plus grande que celle de la liaison Kr-Rb. Le krypton fait partie de la famille des gaz rares ( dernière colonne de la classification périodique ) ; le brome est un halogène ( avant-dernière colonne ) et le rubidium est un métal alcalin ( première colonne ). La différence des nombres d'onde ou des fréquences vibrationnelles est-elle surprenante ? Les gaz rares possèdent une couche électronique externe complète ; en conséquence ils présentent une forte inertie chimique. Dans l'éthanol, on cherche à étudier le mouvement de l'atome d'hydrogène du groupe OH par rapport au reste de la molécule. Donner la formule semi-développée de l'éthanol. Quelles sont alors les masses m1 et m2 à considérer ? H3C---CH2---OH. m1 ( masse de l'atome d'hydrogène ) = 10-3 / (6,02 1023) =1,66 10-27 kg ; m2 (masse du groupe H3C---CH2---O) = 0,045// (6,02 1023) =7,48 10-26 kg. En raisonnant sur la masse réduite µ, montrer que le mouvement de cet atome H est approximativement ce qu'il serait si H était attaché à une masse infinie par une liaison dont la constante de raideur est caractéristique de la liaison OH. En déduire l'expression de la valeur de µ. µ =m1m2/(m1+m2) avec m1 <<m2 d'où µ~m1. µ =1,66 10-27 *7,48 10-26 /(1,66 10-27+7,48 10-26 k) =1,36 10-27 kg. ( à 18 % près on retrouve la masse m1 de l'atome d'hydrogène ). Calculer k pour cette liaison si s = 3600 cm-1. fvib  = 1/(2p)(k/µ)½ = c s ; 1/(4p2)(k/µ) = c2s2 ; k =4p2µc2s2 ; k=4*3,142*1,66 10-27 *9 1016 *(3,6 105)2=7,6 102 N/m. Sachant que le nombre d'onde de la molécule H2 est s = 4160 cm-1, estimer celui de la molécule HD ( où D représente de deutérium, dont le noyau est constitué d'un proton et d'un neutron). On fait l'hypothèse que la constante de raideur de ces deux liaisons sont les mêmes. 1/(4p2)(k/µ1) = c2s12 ; µ1s12=µ2s22=k/(4p2c2). mH mH /(mH+mH)s12=mH mD /(mH+mD)s22 ; mH /(mH+mH)s12= mD /(mH+mD)s22 ; or mD = 2mH d'où :  mH /(mH+mH)s12=2 mH /(mH+2mH)s22 ; s22 =0,75 s12 ; s2 =0,75½s1=0,866 *4160 =3600 cm-1.

menu