Fission, bobine
inductive, écoulement d'un fluide, machine frigorifique, pyromètre.
Concours
technicien de l'industrie et des Mines
2013
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
Fission
de
l'uranium.
23592U + 10n
--->140bXe + a38Sr + 210n.
Déterminer
les entiers a et b.
Conservation du nombre de nucléons : 235+1 = 140+a+2, d'où a =94.
Conservation de la charge : 92 = b + 38, d'où b = 54.
Pourquoi
cette réaction peut-elle engendrer une réaction en chaîne ?
Cette réaction produit plus de neutrons qu'elle n'en consomme.
Vérifier
que l'énergie E libérée est de 135 MeV par la fission d'un noyau
d'uranium 235.
Variation de masse Dm = m(14054Xe)+m(9438Sr)+m(10n)-m(23592U).
Dm =139,925 + 93,915
+1,009-234,994 = -0,145 u ou -0,145 *1,67 10-27 =-2,4215 10-28
kg.
E = Dm c2 = -2,4215
10-28 *(3 108)2 = -2,179
10-11 J ou -2,179
10-11 /(1,6 10-13) = -136 MeV.
En déduire l'énergie
libérée par la fission de 1,0 g d'uranium 235.
Masse d'un noyau d'uranium 235 : 234,994*1,67 10-27 =3,924 10-25
kg.
Nombre de noyau dans 1,0 g d'uranium 235 : 1,0 10-3 / (3,924
10-25)
=2,55 1021.
Energie libérée : E'=-2,179
10-11 *2,55
1021= -5,55 1010 J.
Le signe moins traduit la libération d'énergie dans le milieu extérieur.
Calculer la masse de
pétrole produisant la même quantité d'énergie.
La combustion d'une masse de 1 kg de pétrole produit 42 MJ= 42 106
J.
5,55
1010 /(42 106) =1,3
103 kg.
Bobine inductive.
On se propose d'étudier le circuit ci-dessous. L'interrupteur K est
initialement ouvert. On utilise un oscilloscope à mémoire pour
visualiser les tensions. E = 6,0 V ; R = 50 ohms.
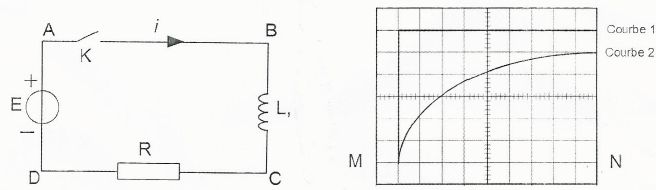
Sensibilité verticale sur les deux voies : 1 V /div ; balayage : 0,1
ms/div. L'origine des tensions est la droite MN.
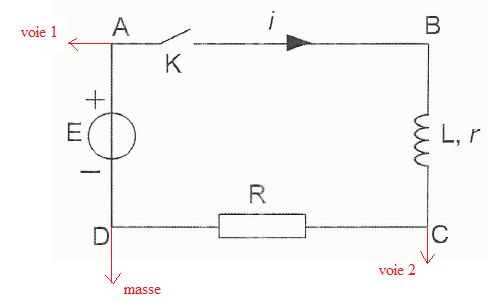
On souhaite à la fermeture de l'interrupteur, visualiser la tension aux
bornes du générateur et celle aux bornes du conducteur ohmique. Indiquer les
branchemants à effectuer.
Pourquoi
utilise-t-on un oscilloscope à mémoire ?
On ferme une seule fois l'interrupteur : le phénomène n'est pas
périodique.
Identifier
les tensions visualisées à l'écran en justifiant.
Courbe 1 : tension continue aux bornes du générateur de tension
continue.
Courbe 2 : tension aux bornes du résistor, image de l'intensité au
facteur R près ; retard à l'établissement du courant.
Exprimer
la tension aux bornes de la bobine. uBC = uL
= Ldi/dt +ri.
Montrer
qu'en régime permanent le courant i tend vers une valeur constante I0 que l'on déterminera.
En
déduire la valeur de r.
En régime permanent dI0/dt est nulle et uL = rI0.
(R+r)I0 = E ; RI0 = 1 V ; I0 = 1/50 =
0,02 A et r = 5/0,02 = 250 ohms.
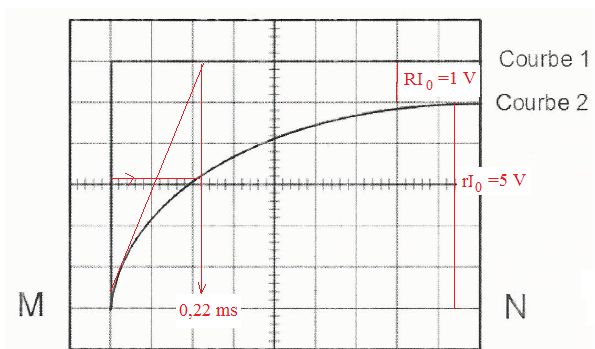
Déterminer
graphiquement la constante de temps t = L/(R+r) et en
déduire L.
t = 0,22 ms = 2,2
10-4 s ; L = t(R+r)
= 2,2 10-4 *300 =6,6 10-2 H.
|
| .
. |
|
|
Vitesse d'écoulement d'un fluide.
On
se propose de déterminer la vitesse d'écoulement, notée u, d'un fluide
dans une canalisation. On place en deux points A et B de la
canalisation deux transducteurs sonores T1 et T2 pouvant fonctionner indifféremment en émetteur et en récepteur d'ultrasons. A l'aide d'un oscilloscope on mesure la durée q que mettent les ultrasons pour parcourir la distance L qui séparent A et B.
Dans le fluide au repos, les ultrasons se propagent à la vitesse V.
Dans le fluide en mouvement à la vitesse u, les ultrasons se propagent :
- à la vitesse V+u dans le sens de déplacement du fluide,
- à la vitesse V-u dans le sens opposé.
Etablir l'expression litérale de la durée q1 mise par les ultrasons pour aller de A en B. q1 = L /(V+u).
Etablir l'expression litérale de la durée q2 mise par les ultrasons pour aller de B en A. q1 = L /(V-u).
En déduire t = q2-q1.
t = L(1/(V-u) -1/(V+u) =2Lu/(V2-u2).
Or u << V, d'où t =2Lu / V2 ; u =tV2 / (2L).
A.N : L = 2,00 m ; V = 1,5 103 m/s ; t = 5,0 µs.
u = 5,0 10-6*(1,5 103)2 / 4,00 =2,8125 ~2,8 m/s.
Calculer le débit volumique en unité SI puis en m3 /h. Diamètre de la conduite D = 30 cm.
Qv = pD2/4 u = 3,14 *0,302 / 4*2,8125 = 0,1988 ~0,20 m3 /s ou 0,20 *3600 = 7,2,102 m3/h. |
.
|
|
Machine frigorifique.
Une machine frigorifique à air, utilisée pour le stockage à basse température de produits chimiques est schématisée ci-dessous :
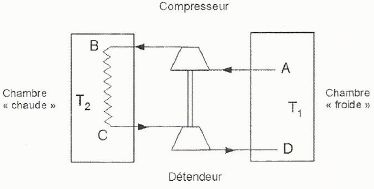
Elle est destinée à maintenir une chambre froide à la température T1. Une masse m = 1,0 kg d'air, prélevé dans la chambre froide à la température TA = T1
est comprimée adiabatiquement. L'air passe ensuite dans un échangeur
plongé dans une pièce dite chambre chaute dont la température T2, supérieure à T1, est considérée comme constante. L'air est ensuite détendu adiabatiquement et renvoyé à la température TD, dans la chambre froide où il va se réchauffer jusqu'à la température T1
considérée comme constante dans toute la chambre froide. Les pressions
de l'air dans l'échangeur et dans la chambre froide sont constantes et
la température de l'air en C est celle de la chambre chaude. Le travail
fourni par le fluide au cours de sa détente est intégralement utilisé
par le compresseur. L'air est considéré comme un gaz parfait et les
transformations sont réversibles. T1 = 268 K ; T2 = 293 K ; PA = 1,0 bar ; PB = 2,0 bar ; Cp air = 1,0 kJ kg-1 K-1 ; g = 1,4.
Tracer sur un diagramme de Clapeyron ( ou diagramme PV) le cycle décrit par l'air.
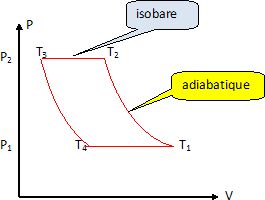
Vérifier que la température TB de l'air après la compression adiabatique est égale à 327 K.
PV = nRT ; V = nRT/P ; PVg =P (nRT)g/ Pg ; P(1-g) Tg = 1/(nR)g = K' ; T P(1-g)/g =K' ; ß =( 1-g1)/g = -0,4 / 1,4 =-0,2857.
Adiabatique réversible A--> B : PAß TA =PBß TB ; TB = TA (PA/PB )ß =268*0,5-0,2857=326,7~327 K.
Déterminer la température TD de l'air après la détente adiabatique.
Adiabatique réversible C-->D : PCß TC =PDß TD ; PBß T2 =PAß TD ; TD = T2 (PB/PA )ß =293*2-0,2857=240,36~240 K.
Pour les 4 transformations envisagées, exprimer le transfert thermique associé pour 1 kg d'air en fonction des températures.
QAB = QCD=0, adiabatiques.
Isobare B--> C : QBC =Cp air ( TC-TB) =Cp air ( T2-TB) ; Isobare D--> A : QDA =Cp air ( TA-TD)=Cp air ( T1-TD).
En déduire le travail W reçu par cycle et par kilogramme d'air.
W + QBC +QDA =0 ; W = -(QBC +QDA) = -1,0(293-327+268-240)= + 6,0 J.
Soit h l'efficacité de la machine. Définir h, l'exprimer en fonction des transferts thermiques et la calculer.
Efficacité : rapport du gain sur l'énergie dépensée h=QDA /W=QDA / (-QBC -QDA) = (TA-TD) / 6,0=(268-240) /6,0 ~ 4,7.
|
|
Pyromètre.
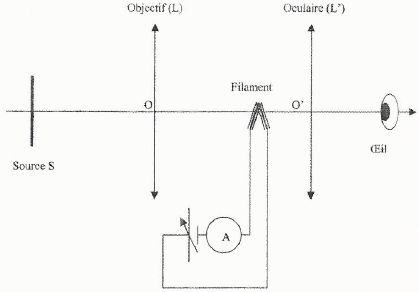
Pour mesurer à distance la température TS d'une source, on
utilise un pyromètre optique à disparition de filament ( gamme de
mesure 500°C - 5000 °C ). Le principe consiste à comparer l'exitance de
l'image de la source avec l'exitance d'un filament préalablement
étalonné, la mesure de l'intensité du courant électrique dans le
filament permet d'accéder à la température. L'exitance est la puissance
totale émise par le rayonnement par unité de surface. Si le filament
apparaît en plus clair ou en plus sombre que l'image de la source, sa
température est supérieure ou inférieure à Ts. Lorsque le filament disparaît, les températures sont identiques.
Proposer une unité pour l'exitance. Puissance en watt par unité de surface en m2, donc W m-2.
Rappeler les formules de conjugaison et de grandissement avec origine au centre optique. Calculer D =SO. on donne la fistance focale de l'objectif f' = 10 cm et le filament se trouve à une distance d = 15 cm de l'objectif.
Appliquer la formule de conjugaison
à l'objectif L :
1/f' = 1/d - 1/(-D) avec 1/f' =
1/0,1 = 10 d
; d = 0,15 m.
1/D = 1/f'-1/d = 10-1/0,15 = 3,33 soit D= 1/3,33=0,3 m =
30 cm.
L’oculaire (L’) a une vergence v= 5
d.
à quelle distance OO'
faut-il placer cette lentille pour observer l’image de
la source et le filament
confortablement
?
L'oeil observe sans fatigue
à l'infini.
L'image définitive doit donc
se située à l'infini ; l'image
intermédiaire de la source et le filament doivent
donc être dans le plan focal objet de l'oculaire
L'.
Appliquer la formule de conjugaison
à l'oculaire : on note A1B1,
l'image intermédiaire et A'B' l'image
définitive.
Les distances algébriques
sont écrites en gras et en
bleu.
5 =
1/O'A'
-
1/O'A1
avec
1/O'A'
= 0 ( image à l'infini ).
d'où
O'A1
= -1/5 = -0,2 m.
OO'
= O
A1+A1O'
= 0,15 +0,2 = 0,35 m =
35
cm.
|
|
|