Formules du
prisme.
Concours itpe 2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
Un
prisme, constitué par un matériau transparent, homogène, isotrope,
d'indice n = 1,5 et d'angle au sommet A = 60° se trouve plongé dans
l'air d'indice égal à 1,0.
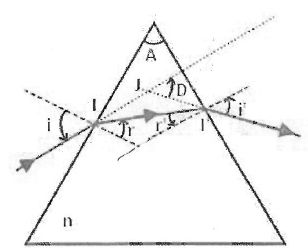
Exprimer les lois de Descartes en fonction de i, i', r, r' et n, traduisant les réfractions à l'entrée et à la sortie du prisme.
Réfraction à l'entrée : sin i = n sin r (1).
réfraction à la sortie : n sin r' = sin i' (2).
Montrer que les angles A et D peuvent s'écrire A = r+r' et D = i+i'-A.
L'angle r a pour complément l'angle BII' ( en notant B le sommet du prisme)
L'angle r' a pour complément l'angle BI'I ; d'où r+r'+ angle BII' + angle BI'I= 180°.
De plus dans le triangle BII' : A + angle BII' + angle BI'I= 180°.
Des angles ayant même supplément sont égaux, d'où : r+r'=A (3)
L'angle D a pour supplément l'angle IJI'.
Dans le triangle IJI' :( i-r )+ (i'-r') + angle IJI' = 180 °.
par suite D= ( i-r )+ (i'-r') = i+i'-(r+r') = i+i'-A(4).
Conditions d'émergence.
On cherche à déterminer l'angle i'lim pour que le rayon lumineux rase le prisme à la sortie en I'.
Que vaut i'lim dans ce cas ?
i'lim = 90°.
On note q la valeur de l'angle r' correspondante. En déduire une relation entre q et n.
(2) donne : n sin q = sin 90 = 1.
Montrer que ilim = sin-1(n sin(A-q).
(3) s'écrit : r =A-q ;
(2) donne : sin ilim = n sin (A-q) soit ilim =sin-1(n sin(A-q).
A.N : 1,5 sin q= 1 ; sin q = 1/1,5 =0,667 ; q = 41,8 °.
lim = sin-1(1,5 sin(60-41,8) =27,9°.
|
| .
. |
|
|
Minimum de déviation.
Expérimentalement, l'étude de D=f(i) montre que la déviation d'un
prisme, d'angle au sommet A constant, éclairé en lumière
monochromatique admety un minimum noté Dm.
En différenciant les 4 équations, déduire une relation entre dD/di, di et di'.
A et n sont des constantes.
cos i di = n cos r dr (5)
cos i' di' = n cos r' dr' (6)
dr +dr' =0 (7)
dD = di + di' (8)
Pour éliminer di', on ajoute : (5) cos r' +(6) cos r :
cos i cos r' di +cos i' cos r di' = n cos r cos r' dr + n cos r' cos r dr'.
cos i cos r' di +cos i' cos r di' = n cos r cos r' dr + n cos r' cos r (-dr)=0.
cos i cos r' di +cos i' cos r di' =0
di' = -cos i cos r' di /(cos i' cos r).
(8) conduit à : dD =di(1-cos i cos r' /(cos i' cos r)).
dD/di = 1-cos i cos r' /(cos i' cos r).
|
.
|
|
On note im, i'm, rm et r'm les valeurs des angles au minimum de déviation.
Quelles relations simples existent entre les angles i'm et im d'une part et rm et r'm d'autre part au minimum de déviation ?
Au minimum de déviation dD/di = 0 ; par suite cos im cos r'm =cos i'm cos rm.
im = i'm et rm = r'm.
La figure est symétrique par rapport au plan bissecteur du prisme.
Exprimer im en fonction de n et A.
rm = r'm = ½A. Par suite sin im = n sin (½A) ; im = sin-1(n sin (½A)).
Donner l'expression littérale de Dm en fonction de A et n.
Dm = im+i'm-A = 2im-A = 2sin-1(n sin (½A))-A.
A.N : im = sin-1(n sin (½A)) = sin-1(1,5 sin 30) =48,6°.
Dm = 2im-A =2*48,6-60 =37,2°.
|
|
|