Bilan énergétique d'une centrale nucléaire :
Concours technicien supérieur de l'industrie et des Mines 2010
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
Bilan
énergétique.
On supposera que chaque tranche de cette centrale fournit une puissance
électrique Ptr telle que |Ptr|
=740 MW. On négligera toutes les pertes d'énergie dans les circuits et
la turbine et on donne les valeurs numériques suivantes aux conditions
de fonctionnement de l'installation. Une centrale nucléaire, simplifiée
à un réacteur nucléaire, est composée de trois circuits distincts :
primaire, secondaire et refroidissement.
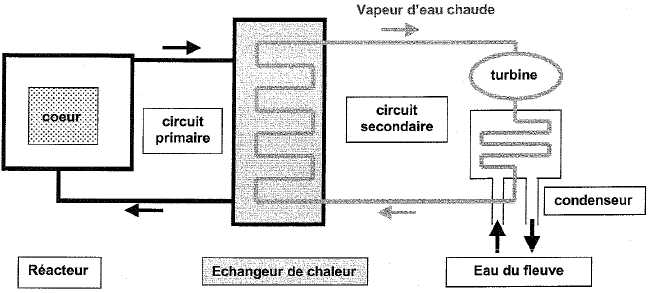
L'énergie
libérée par la réaction en chaîne est extraite du coeur du réacteur par
le fluide caloporteur circulant dans le circuit primaire à la
température q
= 290°C à la pression de 155 bars.
Dans
l'échangeur de chaleur, cette énergie, véhiculée par le fluide
caloporteur, permet de transformer l'eau du circuit secondaire en
vapeur d'eau, à la température qc
=270°C, sous une pression de 56 bars.
La
vapeur d'eau formée entraîne la turbine fournissant un travail
mécanique au rotor d'un alternateur ; celui-ci produit alors l'énergie
électrique.
A la sortie de la turbine, grâce à l'eau du circuit de refroidissement
prélevée froide à la température qf
=10°C dans le fleuve, la vapeur d'eau du circuit secondaire est ramenée
à l'état liquide à la température q'c
= 20 °C dans le condenseur.
Dans le circuit primaire, le fluide caloporteur est de l'eau liquide à
la température q
= 290°C sous haute pression ( 155 bars).
En
comparant les capacités thermiques massiques de l'eau dans les états
liquide et vapeur, expliquer pourquoi il est intéressant de conserver
le fluide caloporteur ( l'eau ) à l'état liquide.
Capacités thermiques massiques de l'eau liquide : c0
=4180 J K-1 kg-1 aux
environs de 10°C sous 1 bar.
c'0 =5250 J K-1
kg-1 aux environs de 290°C sous 155 bars.
Capacités thermiques massiques de
l'eau vapeur : c1 =3800 J K-1
kg-1 aux environs de 270°C sous 56 bars.
c'0 est bien supérieur à c1.
(c'0 = 1,38 c1).
Plus la capacité thermique massique est élevée, plus le fluide est
capable d'extraire de la chaleur du coeur du réacteur.
Pourquoi
la haute pression est-elle nécessaire ?
La haute pression permet de maintenir l'eau à l'état liquide.
Dans la suite de cette partie, on ne tiendra pas compte de l'énergie
apportée par les pompes.
Indiquer,
en prenant comme système l'eau du circuit secondaire, si l'énergie est
transférée par chaleur ou travail et indiquer le signe des énergies
échangées :
DE1
entre l'eau du circuit primaire et l'eau du circuit secondaire.
L'eau du circuit secondaire reçoit de l'énergie sous forme de chaleur
du circuit primaire : DE1
>0.
DE2
entre la turbine et l'eau du circuit secondaire.
La vapeur d'eau du circuit secondaire cède de l'énergie sous forme de
travail à la turbine : DE2
< 0.
DE3
entre le circuit de refroidissement et l'eau du circuit secondaire.
La vapeur d'eau du circuit secondaire
cède de l'énergie sous forme de chaleur à l'eau du fleuve : DE3
< 0.
A
l'aide du premier principe de la thermodynamique, effectuer le bilan
d'énergie, pour un cycle de l'eau du circuit secondaire, en fonction de
DE1,
DE2,
DE3.
La variation de l'énergie interne du fluide est nulle sur le cycle : DE1 +
DE2
+ DE3
= 0.
Donner
l'expression du rendement r du circuit secondaire en fonctions des
énergies échangées.
Le
rendement est le rapport entre l'énergie utile ( travail fourni à la
turbine ) à l'énergie dépensée ( énergie reçue de la part du
circuit primaire ) : r = | DE2|
/ DE1
= | DE2|
/| DE2
+
DE3|.
En
déduire son expression en fonction des puissances P2 cédée à
la turbine et P3 cédée au
fleuve.
r
=|P2 |/ |P2+P3|.
Dans la suite on considérera que P 2 = P tr.(
pertes négligées)..
|
| .
. |
|
|
Le
rendement réel est r = 0,4.
Soit la masse d'eau meau, circulant dans le
circuit de refroidissement pendant l'intervalle de temps Dt.
Etablir
la relation entre meau, Dt, le débit
volumique D dans le circuit de refroidissement et la masse volumique de
l'eau µL.
Débit volumique = volume d'eau / durée = (masse d'eau / masse volumique
de l'eau) / durée.
D = meau / (Dt
µL).
Donner l'expression de l'énergie DE3
entre l'eau du circuit secondaire et le circuit du refroidissement en
fonction de meau, de l'élévation de température
du fleuve Dqf
et de la capacité thermique massique de l'eau de refroidissement.
DE3 =
meau c0
Dqf = D Dt µL
c0
Dqf .
|
.
|
|
Déduire P3
en fonction de D, µL, Dqf
et c0.
DE3 /
Dt
= P3 = D µL
c0
Dqf .
Montrer
que le Dqf
peut se mettre sous la forme Dqf = Ptr
(1-r) / (D µL
c0 r).
r = Ptr / (Ptr +P3
) =Ptr / (Ptr
+D µL
c0
Dqf ) ; r Ptr + rD µL
c0
Dqf = Ptr ; rD µL
c0
Dqf =Ptr- r Ptr ; Dqf =Ptr(1-r) / ( rD µL
c0).
A.N : D = 168 m3/s.
Dqf =740 106
*0,6/(0,4*168*1000*4180)=1,58 ~1,6 °C.
Comme la centrale est équipée de 4 réacteurs ayant un circuit de
refroidissement commun, sachant que l'eau de ce circuit de
refroidissement peut être rejetée loin des berges à condition que sa
température n'exède pas 30°C, le rejet
est-il possible ?
La puissance est multipliée par 4 et tous les autres facteurs restent
constants, en conséquence l'élévation de température de l'eau du fleuve
sera 4*1,58 = 6,3 °C. Le rejet ne sera sans doute pas possible durant
la période estivale. Il restera possible durant le reste de l'année.
L'alternateur.
Un alternateur de 80 m de long pesant 1200 tonnes est muni d'un rotor
de diamètre d =1,2 m tournant à 25 tours par seconde.
Quelle
est la vitesse angulaire w en rad/s
?
w
= 2 p f =
2*3,14*25 = 157,08~1,6 102 rad/s.
Déterminer
la période T et la fréquence f de ce mouvement.
N= 25 Hz ; T = 1/N = 1/25 = 4,0 10-2 s.
Calculer
la vitesse v d'un point de la périphérie du rotor.
v = w r =w ½d = 157,08 *0,6
=94 m/s.
Déterminer
le nombre de paires de pôles que doit posséder l'alternateur pour
produire une tension alternative de fréquence f = 50 Hz.
p = f / N = 50 / 25 = 2 paires de pôles.
|
Ligne
électrique.
L'alternateur précédent, assimilable à un générateur sinusoïdal,
fournit une puissance moyenne P sous une tension efficace U.
Le facteur de puissance est égal à l'unité. Une ligne électrique, de
résistance linéïque r par conducteur, sert à transporter cette
puissance sur une distance L. On donne r = 0,05 ohm km-1
; L = 50 km ; P =900 MW ; U = 40 kV.
Quelle
est en fonction de r, L, U et P, la puissance totale Pj
perdue par effet Joule dans la ligne ? Faire l'application numérique.
Pj = RI2 avec I = P / U
et r = 2rL ; Pj = 2rL P2/U2
= 2*0,05*50*(900 106)2/
400002=2,5 109 W.
Cette valeur étant supérieure à P, toute la puissance initiale est
perdue en ligne.
Pour diminuer cette perte , le distributeur d'énergie utilise un
transformateur élévateur de tension efficace de sortie U' = 400 kV.
la tension de sortie est sinusoïdale de même pulsation que celle de
l'alternateur ; la puissance moyenne est la même à l'entrée et à la
sortie ;le facteur de puissance est égal à 1 à l'entrée comme à la
sortie.
Déterminer
l'intensité efficace I1 du courant débité par
l'alternateur.
I1 = P / U =900 106 / 40
000 =2,25 104 ~2,3 104 A.
Déterminer
l'intensité efficace I2 du courant dans la ligne
très haute tension.
I2
= P / U' =900 106 / 400 000 =2,25 103
~2,3 103 A.
Le nombre de spires du primaire est N1 = 100.
Calculer
le nombre de spires au secondaire.
Rapport de transformation m = U'/U = 400 / 40 = 10.
m = N2/N1
; N2 = m N1 =10*100 =
1,0 103 spires
Reprendre
le calcul de la puissance Pj perdue dans la
ligne et conclure.
Pj
= 2rL P2/U2 =
2*0,05*50*(900 106)2/ 400
0002=2,5 107 =
25 MW, c'est à dire Pj
/P = 25/900 =0,027 ~3 %.
Pour limiter les pertes en ligne, on transporte l'énergie électrique
sous très haute tension.
|
|