Chute
libre, mouvement parabolique.
Concours kiné Assas 2014
|
|
.
.
|
|
|
|
|
|
|
Un
enfant lâche une balle de tennis supposée ponctuelle, sans vitesse
initiale, de sa fenêtre située à une hauteur h = 6,0 m au dessus d'une
verrière oblique. la balle rebondit sur la verrière, en un point A,
symétriquement par rapport à la normale (n) à la verrière en ce point,
sans changement de valeur de sa vitesse. Elle atteint le sol en un
point B, à une hauteur H = 3,0 m sous la fenètre de l'enfant et à une
distance L= 12 m du pied du mur de l'immeuble.
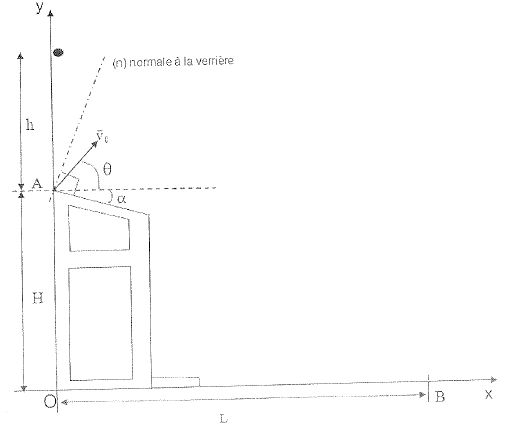
On cherche à déduire l'angle a.
Donner
la relation ente les angles a
et q.
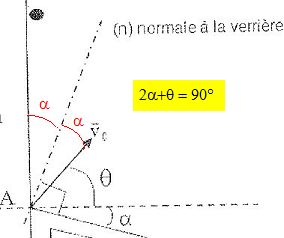
Donner
l'expression littérale de la norme de la vitesse v0 de la
balle à son arrivée en A.
Conservation de l'énergie mécanique entre le départ et A : mgh = ½mv02
; v0 = (2gh)½.
Trajectoire
de la balle entre A et B.
Dééterminer
dans le repère (O, x, y) les équations horaires de l'accélération, de
la vitesse et du vecteur position. L'origine des dates et celle du passage en A.
Accélération ( chute libre ) : (0 ; -g )
Vitesse initiale : v0 cos q ; v0
sin q.
La vitesse est une primitive de l'accélération :
vx = v0 cos q ; vy = -gt + v0
cos q.
Position initiale en A : 0 ; H.
La position est une primitive de la vitesse :
x =v0
cos q t ;
y = -½gt2 +v0
sin q t +
H.
|
|
|
En déduire
l'équation de la trajectoire de la balle.
t = x / (v0
cos q)
;
y = -½g
x2 / (v0
cos q)2
+v0
sin q x
/ (v0 cos q) +H.
y = -½g
x2 / (v0
cos q)2
+
x tan q
+ H.
B est un point de la trajectoire de la balle. Quelle
équation du second degré en tan q obtient-on
?
Au point B, y =0 et x = L.
0 = -½g L2 / (v0 cos q)2
+
L tan q
+ H.
Or 1/ cos2q
= 1+tan2q
:
0 = -½g L2 / v02
(1+tan2q)+
L tan q
+ H.
-½g L2 / v02
tan2q + L tan
q
+ H-½g L2
/ v02=0.
( réponse D).
On divise chaque terme par L : -½g L / v02
tan2q + tan q
+ H/L-½g L
/ v02=0.
|
.
|
|
Quelle est
l'unité du discriminant D
de cette équation du second degré ?
D
= b2-4ac = 1+4(½g L / v02)(H/L-½g L / v02)=
1+2g L / v02(H/L-½g L / v02 )).
D =1+2gL/ v02(H/L-½g L/ v02 )).
Or
v02= 2gh : D =1+L(H/L- L/ (4h) )/
h).
D =1+H/ h- L2/ (4h2).
Le
discriminant est sans dimension.
En
remplaçant v0 par son expression, quelle est
finalement l'expression de l'équation en tan q ?
-½g L / v02
tan2q + tan
q
+ H/L-½g L
/ v02=0.
-½g L /
(2gh) tan2q + tan
q
+ H/L-½g L
/ (2gh)=0.
- L /
(4h) tan2q + tan
q
+ H/L- L
/ (4h)=0.
( réponse B).
A.N
: h = 6,0 m ; H = 3,0 m ; L = 12 m.
-12 / 24 tan2q + tan
q
+ 0,25- 0,5=0.
-0,5 tan2q + tan
q
-0,25=0.
tan2q -2 tan q
+0,5=0.
D'
= 1-0,5 = 0,5 ; D'½
= 0,707 ; tan
q
=1+0,707 = 1,707 ; q
=59,6 ~60°.
tan
q
=1-0,707 = 0,293 ; q
=16,3~16°.
a1 = (90 -q)/2 =(90-59,6)/2=15,2° ~15°.
a2 ==(90-16,3)/2=36,85° ~37°.
|
|
|