Interférences
: détermination d'un indice de réfraction.
Concours kiné Assas 2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
On
réalise une expérience d'interférences lumineuses avec les fentes de
Young éclairées perpendiculairement à leur plan par un faisceau laser
de longueur d'onde l.
Les deux fentes fies F1 et F2 sont séparée d'une
distance "a". On observe la figure d'interférences dans un plan
parallèle au plan des fentes et situé à une distance D
>>a. On considère sur l'écran d'observation un
axe Ox dont l'origine se trouve sur la médiatrice du segment [F1F2],
orienté vers le haut.
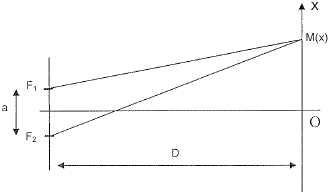
La différence de marche est d
= F2M-F1M = ax/D.
Figure
d'interférences.
A quelle condition sur
d un point
M(x) de l'écran ::
- se trouve une frange
brillante : dFB
= k l
avec k entier relatif.
- se trouve une frange sombre : dFS
= ½(2k+1) l
avec k entier relatif.
Donner
l'expression de l'interfrange
i.
i = l D
/ a.
Quelle
relation existe-t-il entre x et i :
- M(x) se trouve sur une frange
brillante : d = ax/ D = k l
; x = k l D /a ; x = k i.
- M(x) se trouve sur une frange
sombre : d = ax/ D = ½(2k+1) l ; x = ½(2k+1) l
D /a ; x =½(2k+1) i.
|
|
|
La
distance séparant 11 franges brillantes consécutives vaut 5,40 mm.
Calculer
en nanomètres la longueur d'onde de la source laser. a =
1,00 mm et D =1,00 m.
10 i = 5,40 mm ; i = 0,54 mm = 5,4 10-4 m.
i = l D / a ; l = a i / D = 1,00 10-3 *5,4
10-4 / 1,00 =5,40 10-7 m
=540 nm.
Quelle
est la nature de la frange d'abscisse x = -2,97
?
x / i = -2,97 / 0,54= -5,5 = (2k+1) / 2 avec k = -6.
Il s'agit d'une
frange sombre.
Quelle est
la nature de la frange d'abscisse x = 3,78
?
x / i = 3,78 / 0,54=7= k, nombre entier.
Il s'agit d'une
frange brillante.
|
.
|
|
Détermination
de l'indice de réfraction d'un milieu.
Quelle est pour la lumière, l'expression littérale de la durée du
parcours d'un trajet de longueur d dans l'air ?
Dt = d / c.
On
interpose maintenant sur le trajet de la lumière, une lame transparente
d'épaisseur e et d'indice de réfraction n.
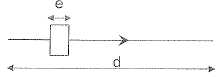
Quelle
est dans ces condition, la nouvelle expression de la durée de parcours
d'un trajet de longueur d dans ces conditions ?
Dt'
=(d-e) / c +
ne /c=d /c +(n-1)e/c = Dt + (n-1)e / c.
On place maintenant devant la fente F1 la lame
transparente décrite ci-dessus.
Soit t = Dt2-Dt1
la différence de durée entre les trajets F2M et F1M.
Exprimer t en
fonction de d, c, e et n.
Dt2=F2M/ c ; Dt1=F1M/ c + (n-1)e / c;
t = F2M/ c - (n-1)e / c -F1M/ c = d / c - (n-1)e / c.
Monter que
la condition d'interférences constructives peut s'écrire t = kT, où
T est la période temporelle de l'onde lumineuse.
d'
=d-(n-1)e = kl
; d'
/ c = d / c - (n-1)e / c
= t
= kl
/ c . Or T = l
/ c : t = kT.
Donner
l'expression de l'abscisse x des franges d'interférences brillantes et
en déduire l'abscisse x0 de la
frange centrale.
t = kT
= d / c - (n-1)e / c.
d = ax/ D ; kT
= ax/ (D c) - (n-1)e / c.
x =k D T c / a +(n-1)e D / a.
x =k D l
/ a +(n-1)e D / a.
x =k i+(n-1)e D / a.
Pour la frange centrale k = 0 et x0 = (n-1)e D / a.
L'ensemble du système de franges est déplacé du côté de la lame.
A.N
: a = 1,00 mm ; D = 1,00 m ; e = 0,100 mm ; x0 =
2,50 cm.
n-1 =x0 a / (eD) ; n = 1+x0 a / (eD).
n = 1+2,50 10-2 *1,00 10-3
/ (1,00 10-4) = 1,25.
|
|
|