Pendule
simple ; projectile ; système GPS et relativité.
Concours kiné Berck 2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
Pendule
simple.
Un pendule simple est formé par un solide ponctuel de masse m, fixé à
un fil inextensible de longueur L et de masse négligeable. Le pendule
est fixé en un point fixe A. On écarte le pendule de la verticale d'un
angle q0
et on le lâche sans vitesse initiale. Il effectue des oscillations non
amorties. On appelle q
l'abscisse angulaire que fait le pendule avec la verticale. On
enregistre les variations de q
en fonction du temps. On donne m = 250 g.
Parmi
les afirmations suivantes, combien y en a-t-il d'exactes ?
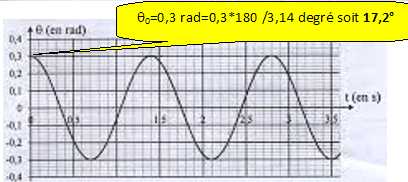
q0
= 15 °. Faux.
La période T est égale à 1,4 s. Vrai.
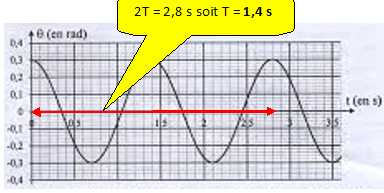
La longueur du fil est L = 49 cm. Vrai.
T = 2 p
(L/g)½ ; L = T2g / (4p2)=1,42*9,81
/(4*3,142) ~0,49 m.
L'énergie potentielle de pesanteur initiale est Epp
= 53 mJ. Vrai.
L'origine de l'énergie potentielle est prise à la position d'équilibre.
Epp = mgL (1-cosq0)=0,25*0,49*9,81(1-cos
17,2) =5,3 10-2 J = 535 mJ.
Au passage à la position d'équilibre
la vitesse vaut v = 0,65 m/s. Vrai.
L'énergie mécanique intiale est
sous forme potentielle et vaut 0,053 J.
A la position d'équilibre l'énergie mécanique est sous forme cinétique
: ½mv2.
Conservation de l'énergie mécanique : 0053 = ½*0,25*v2
; v =0,65 m/s.
|
|
|
Calculer
la valeur de la tension F exercée par le fil sur le solide ponctuel à
la position d'équilibre.
Le
solide est soumis à son poids P = mg et à la tension F du fil.
A la position d'équilibre, ces forces ont même direction mais sont de
sens contraire.
Ecrire la seconde
loi de Newton sur un axe vertical orienté vers le haut.
F-mg = mv2/L ; F = m(g +v2/L)
=0,25(9,81+0,652/0,49) ~2,7 N.
|
.
|
|
Projectile.
A la date t=0, on lance un projectile considéré comme ponctuel, à
partir d'un point O avec une vitesse initiale v0
faisant un angle a
avec l'horizontale. L'objectif d'une caméra est placé dans un plan
horizontal situé à une hauteur H au dessus du sol. le projectile passe
lors de son mouvement ascendant dans le plan de l'objectif à l'instant t1,
puis lors de son mouvement descendant àl'instant t2.
On néglige l'action de l'air sur le projectile. On donne v0
= 10,5 m/s ; a
= 42,3°; Dt
= t2-t1 = 1,02 s.
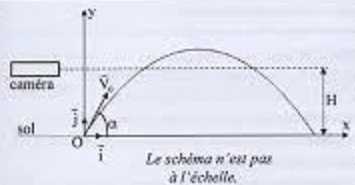
Calculer H.
Equations horaires : x = v0
cos a t ;
y = -½gt2 +v0 sin a t.
On résout l'équation H = -½gt2 +v0
sin a t
ou t2
-2v0 sin a
/ g t +2H/g = 0.
t2
-2*10,5 sin 42,3 /9,81 t +2H/9,81 = 0.
t2
-1,44 t +0,204 H =0
Discriminant D
= 1,442-4*0,204H =2,074-0,8155 H.
t1 = ½(1,44-D½) ; t2 = ½(1,44+D½)
; t2
-t1
=D½ =
1,02 ; D
= 1,022 =1,04.
2,074-0,8155 H
= 1,04 ; H = (2,074-1,04) / 0,8155 =1,27 m.
|
|
|
Relativité
et système GPS.
Le
système GPS est composé d'une constellation de 24 satellites, chaque
satellite étant équipé de plusieurs horloges atomiques. Pour calculer
la position, il faut prendre en compte les effets relativistes. On se
limitera ici au phénomène de dilatation des durées : l'horloge du
satellite va retarder par rapport à la même horloge située sur terre.
On admettra qu'un satellite GPS est en orbite circulaire àl'altitude h
= 20200 km.
Masse de la terre M = 5,97 1024 kg ; rayon
terrestre R = 6,37 103 km.
Dtm
: durée mesurée ; Dtp
: durée propre ; Dtm
= g Dtp ;
g
= (1-v2/c2)-½.
Calculer
la dérive journalière ( en µs de l'horloge atomique du satellite par
rapport à la même horloge sur terre.
Vitesse du satellite : v =( GM / (R+h))½.
v = (6,67 10-11 *5,97 1024
/(6,37 106 +2,02 107))½
=3,87 103 m/s.
Dtp
- Dtm
=(1-g)Dtp.
1-g =1- (1-( 3,87
103/ (3,00 108))2)-½
=8,326 10-11 s.
Dérive journalière : 24*3600*8,326 10-11 ~7,2 10-6
s = 7,2 µs.
|
|
|


