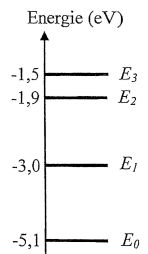
Niveau d'énergie, pendule élastique, projectile, mouvement d'un palet. Concours kiné EFOM 2014 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Niveau d'énergie. Le diagramme ci-dessous donne les premiers niveaux d'énergie de l'atome de sodium. L'état fondamental est caractérisé par une énergie E0. Dans une ampoule contenant de la vapeur de sodium atomique sous faible pression, on trouve un dispositif produisant un faisceau d'électrons d'énergie cinétique réglable. A un photon d'énergie 1,0 eV est associée une onde électromagnétique de longueur d'onde l = 1240 nm. A. Un atome de sodium peut éventuellement être excité par un électron d'énergie cinétique 1,1 eV. Vrai. Si l'atome de sodium se trouve déja à l'état excité E1 où E2 il peut être excité par cet électron. Par contre cela n'est pas possible si l'atome de sodium se trouve à l'état fondamental. B. Un atome de sodium dans son état fondamental peut être excité par un électon d'énergie cinétique 6,0 eV. Faux L'atome de sodium perd un électron, il est ionisé. Un atome de sodium dans l'état excité E1 se désexcite. C. Son énergie diminue. Vrai. D. Il peut produire un photon d'énergie 3,0 eV. Faux. Il émet un photon d'énergie 5,1-3=2,1 eV. E. La radiation produite appartient au domaine visible. Vrai. 1240 / 2,1 =590 nm. Pendule élastique. Un ressort à spires non jointives de constante de raideur k = 10 N / m, de longueur à vide L0 = 20 cm et suspendu verticalement. Lorsque la longueur du ressort est L > L0, le ressort exerce une force de rappel de même direction que le ressort et de sens opposé à l'étirement de celui-ci. La norme de cette force est donnée par F = k(L-L0). On donne g = 10 m s-2. A. Une masse de 100 g allonge le ressort de 10 cm.Vrai. Poids : 0,1*10 = 1 N; allongement :1/10 = 0,1 m = 10 cm. B. Une masse de 100 g allonge le ressort de 30 cm. Faux. On réalise maintenant le montage ci-après avec deux ressorts caractérisés par ( k, L0) et (k', L'0) et accrochés à deux points fixes distants d'une longueur L > L0+L'0. On néglige les dimensions de l'objet devant les longueurs des ressorts. 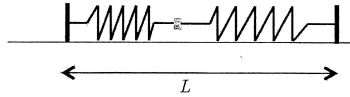C. Si L0 = L'0 le ressort ayant la constante de raideur la plus grande est celui qui est le plus court à l'équilibre. Vrai. A l'équilibre : k(L1-L0) =k'(L2-L0) ; Si k < k', L1-L0 >L2-L0. D. Si k = k', le ressort ayant la plus grande longueur à vide est celui qui est le plus long à l'équilibre. Vrai A l'équilibre : k(L1-L0) =k(L2-L'0) ; L1-L0 =L2-L'0 ; Si L1 < L2, L0 <L'0 . E. Si k = k', le ressort ayant la plus grande longueur à vide est celui qui s'allonge le plus à l'équilibre. Faux. Pour une même constante de raideur et une même force de rappel, l'allongement est identique. Projectile.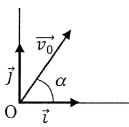 On lance un projectile depuis l'origine du repère avec une vitesse initiale v0. On suppose que le projectile n'est soumis qu'à son poids. A. La durée passée en l'air n'est pas proportionnelle à v0. Vrai. La portée est égale à x = v0 cos a t, soit t = x / (v0 cos a).   B. L'abscisse du point de la trajectoire d'altitude maximale est proportionnelle à v0. Faux. équations horaires x = v0 cos a t ; y =-½gt2 + v0 sin a t. Au sommet de la trajectoire la composante verticale de la vitesse est nulle  -gt + v0 sin a =0  ; t =v0 sin a / g Repport dans y : yS =-½(v0 sin a)2+ (v0 sin a)2 / g = ½(v0 sin a)2/ g. xS =v0 cos a v0 sin a / g = v02sin (2a) / 2g. C. Pour une vitesse initiale donnée, le projectile est envoyé le plus haut possible pour a = 45°. Faux yS = ½(v0 sin a)2 / g est maximal pour a = 90°. D. L'abscisse du point de chute est proportionnelle à v02. Vrai. x = v02sin (2a) / g. D. Le vecteur accélération garde une norme constante. Vrai. Accélération de la pesanteur g en chute libre. . Mouvement d'un palet. On étudie le mouvement d'un palet de masse m = 1 kg glissant sur une rampe de planche à roulettes modélisée par trois portions retilignes. 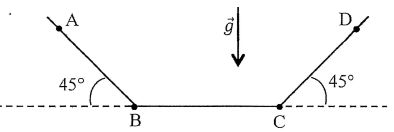Les passages en B et C se font sans modification de la vitesse du palet et on néglige les frottements fluides dans l'air. AB = BC = 1 m cos 45 = sin 45 ~0,7. Le palet est lâché sans vitesse du point A. En l'absence de frottement : A. Le palet atteint le point D situé à la même altitude que A. Vrai. B. Le mouvement est accéléré entre B et C. Faux ( entre B et C aucune force ne travaille, la norme de la vitesse est constante ). Le palet est maintenant soumis à des frottements solides opposés à la vitesse et de norme f constante. Ces frottements sont tels que le palet glisse dès qu'on le lâche. C. Si le palet dépasse B, le mouvement est accéléré entre B et C. Faux. La vitesse diminue du fait des frottements solides. D. Si f = 2N, le palet s'arrête avant d'atteindre le point C. Faux. Hypothèse : le point C est atteint Travail des frottements entre A et C : -f (AB+BC )= -4 J. Energie mécanique en A : mgAB sin 45 =10*1*0,7 = 7 J. Energie mécanique en C : 7-4 = 3 J. E. Si f = 3 N, le palet dépasse le point C. Vrai. Hypothèse : le point C est atteint. Travail des frottements entre A et C : -f (AB+BC) = -6 J. Energie mécanique en A : mgAB sin 45 =10*1*0,7 = 7 J. Energie mécanique en C : 7-6 = 1 J.

menu