Oscillations
mécaniques, pendule, propagation d'une onde : concours audioprothésiste
Nancy 2005
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
Oscillations
mécaniques.
On dispose d'un solide de masse m =150 g avec laquelle on réalise
successivement 2 montages :
montage
1 : on associe la masse à un ressort ; montage 2 : on constitue un
pendule simple. Pour les deux montages, on enregistre les oscillations.
Identidier
chaque courbe.
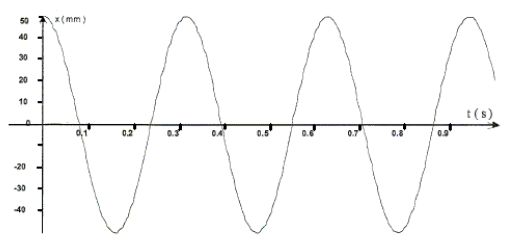
Oscillateur élastique : on représente
l'abscisse x du centre d'inertie de la masse en fonction du temps.
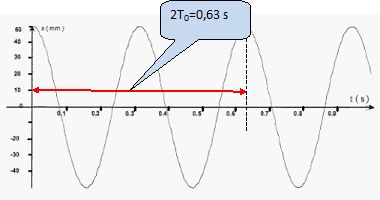
Pendule simple : on
représente l'amplitude angulaire en fonction du temps.
Les
frottements sont-ils négligeables ? Expliquer.
L'amplitude reste constante au cours du temps, les frottements sont
négligeables..
Déterminer
graphiquement la période propre. ( voir graphes ci-dessus
).
En
déduire la longueur du pendule et la raideur k du resort.
On
prendra g = 9,81 m s-2.
T0 = 2p(m/k)½ ; k = 4p2m/T20
=4*3,142*0,150 / 0,82=9,25
~9,3 N m-1.
T0 = 2p(L/g)½ ; L =gT20
/(4p2)= 9,81 *12 /(4*3,142)~0,25 m.
|
|
|
Calculer
dans chaque cas, les énergies potentielles maximale et minimale.
L'origine
des l'énergie potentielle est prise au passage à la position
d'équilibre. A cette position, l'énergie potentielle est minimale et
vaut zéro.
Oscillateur élastique : Ep = ½kx2max
; xmax = 0,5 cm = 5 10-3
m ( lecture graphe).
Ep
=0,5*9,25*(5 10-3)2=1,156
10-4 ~1,2 10-4 J.
Pendule : Ep=mgL(1-cos q0)
; q0=
10° ( lecture graphe ).
Ep=0,15*9,81*0,25(1-cos
10) ~5,6 10-3 J.
Que
peut-on dire pour les deux systèmes :
- de l'évolution de l'énergie mécanique.
En absence de frottement l'énergie mécanique du système reste constante.
- de l'évolution temporelle de l'énergie cinétique par rapport à
l'énergie potentielle.
L'énergie mécanique est la somme de l'énergie cinétique et de l'énergie
potentielle.
Energie cinétique et énergie potentielle varient ens sens inverse.
|
.
|
|
Propagation
d'une onde.
Pour
mesurer la célérité d'un signal transversal le long d'une corde, on
utilise deux cellules photoélectriques A et B, distantes de 2 m et
reliées à un chronomètre électronique.
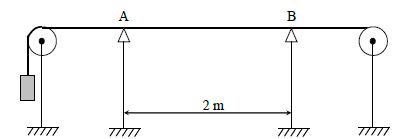
Il
est posible de faire varier la tension de la corde ( force exercée par
la masse suspendue ) et de mesurer la valeur T de cette tension. On
peut également utiliser des cordes de masses linéiques différentes.
Expliquer
le principe de l'expérience permettant de mesurer la célérité c du
signal transversal le long de la corde.
La
distance AB est connue. Pour déterminer la durée de la
propagation
du signal entre A et B, la première cellule photoélectrique déclenche
le chronomètre au passage du signal, tandis que la seconde cellule
provoque l'arrêt du chronomètre au passage du signal.
Donner
l'expression littérale de la realtion qui lie la durée Dt de la
propagation du signal entre A et B, la distance d = AB et la célérité c
du signal.
d = c Dt.
Au cours d'une première expérience, la masse linéique de la corde est µ
=0,1 kg m-1. On mesure Dt pour différentes
valeurs de la tension T.
Compléter
la troisième ligne du tableau suivant.
| T(N) |
40 |
20 |
15 |
10 |
| Dt(s) |
0,10 |
0,14 |
0,16 |
0,20 |
| c
(m/s) |
2/0,10 =
20 |
2/0,14~14,3 |
2/0,16
=12,5 |
2/0,20
=10 |
| c / T½ |
20/40½
=3,16 |
14,3 / 20½
=3,20 |
12,5 / 15½
=3,22 |
10 / 10½
=3,162 |
La
célérité est-elle une fonction croissante de la tension de la corde
?
La célérité et la tension varient dans le même sens. La célérité est
une fonction croissante de la tension.
La
célérité est-elle une grandeur proportionnelle à la tension
de la corde ?
Non, quand la tension double, la célérité ne double pas. Quand la
tension quadruple, la célérité double.
Au cours d'une seconde expérience, la tension de la corde est T = 40 N.
On mesure la durée Dt
pour différentes cordes. Compléter
la troisième ligne du tableau.
| µ(kg
m-1) |
0,10 |
0,40 |
1,6 |
1,0 |
| Dt(s) |
0,10 |
0,20 |
0,40 |
0,32 |
| c
(m/s) |
2/0,10 =
20 |
2/ 0,2~10 |
2/0,4 =5 |
2/0,32
~6,3 |
| c µ½ |
20*0,10½=6,32 |
10*0,40½=6,32 |
5*1,6½=6,32 |
6,3*1½=6,3 |
Quelle
est la grandeur caractéristique de chaque corde ?
La masse linéique µ est une caractéristique de chaque corde.
La
célérité est-elle une fonction croissante de la masse linéique de la
corde.
La célérité et la masse linéique varient en sens contraire. La célérité
n'est pas une fonction croissante de la masse linéique. |
|
Modélisation.
On souhaite vérifier que la valeur de la célérité du signal le long de
la corde est donnée par c = (T / µ)½.
Montrer
que cette relation est cohérente avec les réponses précédentes.
Voir les quatrièmes lignes de chaque tableau.
Montrer
par analyse dimensionnelle que la grandeur ( T/µ)½
est homogéne à une vitesse.
T est une force, c'est à dire une masse fois une accélération : [T]= M
L T-2 ; µ est une masse par unité de longueur :
[µ]= M L-1.
[T/µ]=L2
T-2[(T
/ µ )½]=L T-1 ( m s-1).
Vérifier,
à partir d'un exemple numérique de la seconde expérience, que cette
relation permet de retrouver la valeur expérimentale de c.
T = 40 N ; µ =0,1 kg m-1 ; c =(40/0,1)½
= 20 m/s.
Acoustique.
La figure suivante reprsente la variation temporelle de la pression
acoustique en un point donné. Cette variation caractérise une onde
acoustique sinusoïdale qui se propage.
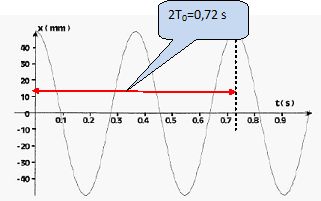
Déterminer
la période T, la fréquence f et la longueur d'onde l ; c = 340 m/s.
T = 0,025 s ; f = 1/T = 1/0,025 = 40 Hz ; l = c T =340
*0,025 =8,5 m.
Déterminer
la pression efficace peff de l'onde
acoustique.
pmax = 1 Pa, lecture graphique ; peff
= pmax / 2½
=1/1,414 = 0,707 ~0,71 Pa.
Calculer
le niveau sonore de l'onde acoustique étudiée.
L = 20 log( peff / p0)
avec p0 = 2 10-5 Pa.
L = 20 log(0,707 /(2 10-5))~91 dB.
|
|
|
|