Super héros en
danger.... Bac
S Amérique du Nord 2015
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
|
|
|
|
Rocketer utilise un
réacteur placé sur son dos pour voler.
Données : vitesse constante du fluide éjecté vf = 2 103
m/s ; masse initiale du système : mr = 120 kg dont 40
kg de fluide au moment du décollage ;
débit massique du fluide constant Df = mf /
Dt où mf
est la masse de fluide éjecté pendant la durée Dt ; les frottements de
l'air sont supposés négligeables.
Propulsion par
réaction.
Lorsqu'un moteur expulse vers l'arrière un jet de fluide, il apparaît
par réaction une force de poussée dont la valeur est égale au produit
du débit massique de gaz ejecté par la vitesse d'éjection des gaz.
Rocketer réalise quelques essais de mouvements ascensionnels verticaux.
Le mouvement est composé de deux phases : phase 1 : durant Dt1 = 3,0 s il
passe de l'immobilité à la vitesse v1, vitesse qui reste
constante au cours de la phase 2.
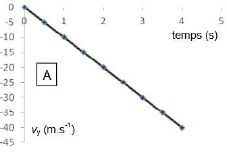
Pour la phase 1, donner la direction et le sens du vecteur accélération
aG du système. Que dire de l'accélération durant la phase 2
? Justifier.
Phase 1 : la vitesse
croît, l'accélération a le sens de la vitesse, vertical vers le haut.
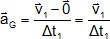
Phase 2 : la vitesse est
constante, le mouvement est rectiligne uniforme : l'accélération est
nulle.
Etude de la phase
1.
On assimile Rocketeer et son équipement à un système noté M dont on
néglige la variation de masse ( due à l'éjection de gaz ) durant la
phase 1.
Juste après le décollage, la force de poussée F est l'une des forces
s'exerçant sur le système. Quelle est l'autre force s'exerçant sur le
système ?
Le poids, verticale, vers
le bas, valeur P = mr g = 120 *10 = 1,2 103 N.
Trois valeurs d'intensité de force de poussée sont proposées. Justifier
que seule la proposition C permet le décollage. A : 800 N ; B : 1200 N
; C : 1600 N.
Pour décoller, il faut
que la poussée soit supérieure au poids P.
En supposant que la poussée soit égale à 1600 N, montrer que la masse
du fluide consommé durant la phase 1 est égale à 2,4 kg.
La
valeur de la poussée est égale au produit du débit massique de gaz
ejecté par la vitesse d'éjection des gaz. F = mf / Dt1 *vf ;
mf
=F Dt1 / vf = 1600 *3,0 / (2 103)=2,4
kg.
Déterminer l'accélération de Rocketeer et en déduire v1.
Suivant un axe vertical ascendant, la seconde loi de Newton s'écrit :
F-P = mr a.
a = (F-P) / mr =(1600-1200) / 120 = 3,333 ~3,3 m s-2.
v1 = a Dt1 =3,333 *3,0
= 10 m s-1.
|
| .
. |
|
|
Problème technique.
Après quelques dizaines de mètres, le jet-pack ne répond plus et tombe
en panne. Au bout de 80 m d'ascension verticale, la vitesse de
Rocketeer est nulle. Il amorce alors un mouvement de chute verticale.
La position du système est repéré sur un axe vertical dirigé vers le
haut et la date t=0 correspond au début de la chute, soit à l'altitude y0
= 80 m.
Les graphes suivants proposent quatre évolutions de la vitesse vy,
suivant l'axe Oy, du système au cours du temps. Quelle est la
représentation cohérente ?
Le système est en chute
libre ( les frottements de l'air étant négligés), la valeur de la
vitesse est une fonction croissante du temps vy
= -10 t. La vitesse initiale étant nulle.
La vitesse est dirigée
vers le bas, en sens contraire de l'axe Oy.
Montrer que lors de la chute, la
position de Rocketeer est donnée par : y(t) = -5t2+80.
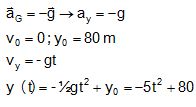
|
.
|
|
A 10 kilomètres du lieu de décollage, Batman, alerté dès le début de la
chute de Rocketeer saute dans sa Batmobile, véhicule se déplaçant au
sol.
Quelle doit être la valeur minimale de la vitesse moyenne de la
Batmobile pour sauver Rocketeer ? Commenter.
Durée de la chute de
Rocketeer : 0 = -5t2+80 ; t = 4 s.
Vitesse moyenne minimale
de la Batmobile : 10 103 / 4 =2,5 103
m/s soit 2,5 103*3,6 = 9,0 103
km/h.
Cette vitesse ne
correspond pas à la vitesse d'une voiture réelle ; avec une telle
vitesse, la batmobile risque de décoller.
|
|