L'indigo
: synthèse, teinture. Bts QIABI 2015
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
A.
L'indigo, une couleur, mais aussi une molécule.
A.1.1.
Entourer les fonctions alcool de la molécule d’isatan B et préciser
leur classe.
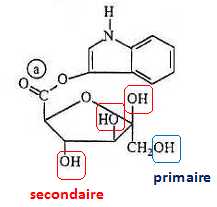
A.1.2.
Déterminer la formule brute de l’indoxyle.
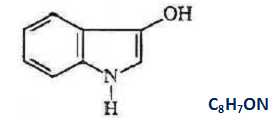
A.2.1.On
s’intéresse à la formation de l’indigo par oxydation de l’indoxyle.
A.2.1.a)
Écrire la demi-équation électronique pour le couple (indigo/indoxyle)
en milieu acide en utilisant les formules brutes des molécules.
Indigo C16H10N2O2
+4H+ +4e-
=2 C8H7NO.
A.2.1.b)
Écrire la demi-équation électronique pour le couple (O2 /
H2O) en milieu acide.
O2 +4H++4e-
= 2H2O.
A.2.1.c)
Écrire l’équation de la réaction qui a lieu lors de la formation de
l’indigo.
C16H10N2O2
+
2H2O
=2 C8H7NO +O2.
A.2.2. Expliquer
pourquoi l'indigo est une substance colorée.
La molécule comporte un grand nombre de doubles liaisons conjuguées (
groupes chromophores C=C et C=O).
B.
Synthèse de l'indigo.
B.1. Donner
deux raisons permettant de justifier l'utilisation d'indigo de
synthèse (une des raisons devra s’appuyer sur un calcul).
Il
faut cueillir environ 700 kg de plantes pour obtenir 1 kg de pigment
indigo. Le procédé dure plusieurs mois. La production mondiale est de
14000 tonnes.
Il faudrait donc cueillir 700*14000 *1000 = 9,8 109
kg de plantes. C'est impossible.
Un chimiste doit mettre au point les conditions de synthèse de l'Indigo
afin d'améliorer le rendement de cette production au sein de son
entreprise.
Il réalise pour cela le protocole expérimental donné.
Dans
la synthèse, on utilise de l’acétone (aussi appelée
propanone).
B.2.1.a)
Indiquer la verrerie que le chimiste doit utiliser pour
prélever l'acétone.
On prélève environ 10 mL d'acétone, volume peu précis, à l'aide d'une
éprouvette graduée.
B.2.1.b)
Donner la formule semi-développée de l’acétone.
H3C-CO-CH3.
B.2.1.c)
L’analyse du spectre RMN de l’acétone montre un unique
singulet vers 2,2 ppm. Justifier cette observation et comparer la
valeur de ce déplacement chimique à celle des protons
d’un alcane.
L'acétone
possède six protons équivalents, le carbone voisin ne comporte pas de
proton. Donc un singulet. En alpha des groupes méthyles se trouve le
groupe carbonyle C=O, déblindant, d'où le déplacement chimique observé
( 2,2 ppm au
lieu de de 1 ppm dans le cas des alcanes )
B.2.1.d)
Sur le spectre infra-rouge de l’acétone, on observe une bande
d’absorption vers 1 700 cm-1, cette bande n’est
plus présente sur le
spectre du produit obtenu après réduction de l’acétone.
À quelle liaison est due cette bande à 1 700 cm-1
sur le spectre
infra-rouge ?
La bande fine et intense à 1700 cm-1 est due à
la présence du carbonyle C=O.
B.2.2. Légender
le schéma du
montage de la filtration sous vide, en utilisant les mots contenus dans
la liste suivante : filtrat, fiole à vide, papier filtre, entonnoir
Büchner, trompe à vide, excipients solides.
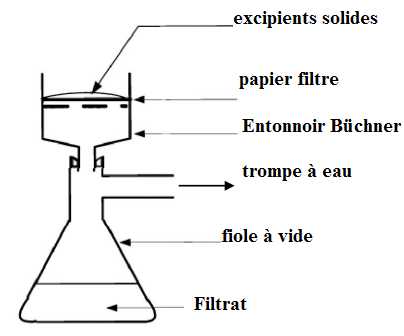
B.2.3.
Expliquer pourquoi la filtration sous vide est préférée à une
filtration simple.
La filtration sous vide créée une dépression dans la fiole à vide. Le
liquide passe rapidement dans la fiole à vide.
B.2.4.
Le chimiste souhaite déterminer le rendement de cette synthèse sachant
que la masse d'indigo mi obtenue après séchage
est de 0,49 g.
Données
: masses molaires (en g.mol-1) : M(indigo) = 232
; M(2-nitrobenzaldéhyde) = 151 ;
masse volumique de l’acétone : r =
0,79 g.cm-3.
Montrons que
le 2-nitrobenzaldéhyde est le réactif limitant :
n = m / M(2-nitrobenzaldéhyde) = 1,00 / 151 =6,62 10-3
mol.
n(acétone) = r
V / M(acétone) =0,79 *10 / 58 = 0,28 mol.
n(soude) = 0,004*2 = 0,008 mol.
Le 2-nitrobenzaldehyde, la soude et l'acétone réagissent mole à mole :
le 2-nitrobenzaldehyde
est le réactif limitant.
Calcul
de la masse maximale d'indigo attendue.
A partir de 2 moles de 2-nitrobenzaldehyde
on obtient une mole d'indigo.
n(indigo) =0,5* 6,62 10-3
=3,31 10-3 mol.
Masse d'indigo attendue m = 3,31 10-3
232 =0,768 g.
Le rendement
r est le rapport entre la masse d'indigo obtenue et la masse d'indigo
attendue si la réaction était totale.
r = 0,49 / 0,768 ~0,64 (64 %).
B.2.5.
Le chimiste veut ensuite déterminer la masse de 2-nitrobenzaldéhyde
nécessaire à la production de 100 kg de pigment. Préciser le calcul
qu’il doit effectuer et faire l’application numérique.
1,0 g de 2-nitrobenzaldéhyde
conduit à 0,49 g d'indigo.
100 /0,49 =204 ~2,0 102 kg.
|
| .
. |
|
|
C. La
couleur indigo.
B.3.1.
Répondre par VRAI ou FAUX aux affirmations suivantes. Pour les
affirmations fausses, justifier et corriger.
a)
La lumière blanche est monochromatique. Faux.
La lumière blanche contient toutes les couleurs de l'arc en ciel, elle
est polychromatique.
b)
Le prisme disperse la lumière par diffraction. Faux.
La réffraction : le verre est un milieu dispersif pour la
lumière blanche.
c)
Les radiations de la lumière visible ont une longueur d'onde
comprise entre 400 nm et 800 nm. Vrai.
d)
L'indice de réfraction du prisme dépend de la longueur d'onde de la
radiation lumineuse. Vrai.
e)
La fréquence d'une radiation monochromatique de couleur
violette
est supérieure à celle d'une radiation de couleur rouge. Vrai.
Le spectre obtenu par le chimiste est représenté ci-dessous.
B.3.2.a)
Nommer les grandeurs portées sur les axes (en ordonnée et en abscisse)
et donner leur unité.
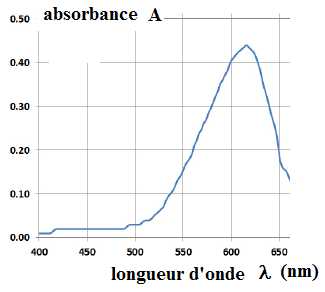
B.3.2.b)
Ce spectre permet-il de justifier la couleur de l'indigo ?
L'absorption est maximale vers 620 nm (orangé) ; l'indigo est bleu,
couleur complémentaire de l'orangé..
|
|
|
|
Dosage spectrophotométrique.
L’amateur de bonbons dissout un bonbon dans l'eau d'une fiole jaugée de
50 mL. Il obtient une solution B.
Il réalise ensuite une échelle de teintes à partir d'une solution mère
de colorant de concentration cMère = 34,5
µmol.L-1.
Les concentrations des solutions réalisées sont données dans le tableau
ci-dessous :
| Solutions
filles |
1 |
2 |
3 |
4 |
5 |
| Concentrations
( µmol/L) |
1,14 |
2,72 |
4,08 |
5,44 |
6,80 |
Après mesure de l'absorbance de
chaque solution fille, il trace la courbe représentant l'absorbance A
en fonction de la concentration c exprimée en µmol.L-1.
C.1.1.
Donner le nom général de ce type de courbe.
Il s'agit d'une courbe d'étalonnage.
C.1.2.
Il obtient une droite d'équation: A = 83,7.10-3
× c
Citer la loi mise en évidence.Loi de Beer-Lambert.
C.2.
Combien de bonbons par jour ?
L'absorbance de la solution B mesurée est : Ab =
0,518
Déterminer le nombre de bonbons nb que cet
amateur qui pèse 70 kg peut consommer par jour sans risque pour sa
santé. Conclure.
Données : masse molaire de E132 : M(E132) = 466 g.mol-1
; DJA (E132) = 5 mg / kg.
cb = Ab
/(87,3 10-3) =0,518 / (87,3
10-3)=6,18 µmol/L soit 6,18 10-6
*0,050 ~3,1 10-7 mol E132 dans un bonbon.
Masse E132 dans un bonbon : 3,1
10-7 *466 =1,44 10-4 g =
0,144 mg.
Il peut consommer chaque jour : 5*70 / 0,144 ~ 2,4 103
bonbons.
Teinture
à l'indigo.
"La teinture à l’indigo, c'est un tour de magie. La couleur bleue
n'apparait que lorsqu'on enlève le tissu de la cuve ! "
D.1.1.
Indiquer la couleur du bain de teinture en justifiant la réponse.
L’indigo (Ind) est insoluble dans l’eau. On utilise alors une forme
réduite appelée leucodérivé (IndH2), jaune et
soluble dans l’eau.
D.1.2.
Rédiger le texte du mail (en 5 lignes maximum) que vous allez envoyer
au vendeur lui expliquant le "tour de magie". Utiliser un vocabulaire
scientifique précis.
L'indigo, insoluble dans l'eau, ne permet pas de fabriquer une
teinture. Par contre la forme réduite IndH2 du
couple oxydant / réducteur (Ind / IndH2) est
soluble et de couleur jaune. Tant que le tissu reste dans le bain, il
prend une couleur jaune. A sa sortie du bain, la forme IndH2
est oxydée par le dioxygène de l'air en Ind, de couleur bleue.
D.1.3.
Placer les 3 couples (oxydant / réducteur) intervenant sur l’axe de
potentiel standard.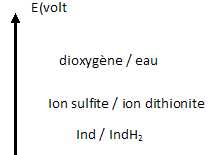
Observation au microscope.
On
peut distinguer les fibres naturelles des fibres synthétiques au
microscope par leur contour caractéristique. Les fibres de soie ont une
surface plane avec des irrégularités, ce qui les distingue des fibres
synthétiques dont la surface est plus régulière. L’image obtenue avec
l’objectif 40X est représentée ci-dessous :

Le diamètre moyen de ce fil de soie est estimé à 50 µm.
D.2.2.1. Justifier que cette estimation est en accord avec l’image obtenue au microscope.
L'échelle indique : 8 mm correspondent à 200 µm. Le diamètre du fil est de 2 mm soit 50 µm.
D.2.2.2. Calculer le diamètre apparent (en rad) à l'oeil nu de la fibre à la distance minimale de vision distincte dm = 25 cm.
La fibre est-elle visible à l'oeil nu ?
50 10-6 / 0,25 =2 10-4 rad.
Cette valeur est inférieure au pouvoir de résolution de l'oeil qui est de 3.10-4 rad. La fibre n'est pas visible à l'oeil nu.
D.2.3. Peut-on affirmer que la fibre est bien de la soie naturelle ?
Non, la surface de la fibre est trop régulière.
|
|
|
|