QCM électricité. Concours CPR 2014

QCM électricité. Concours CPR 2014

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

.
.

Réponse d'un circuit RLC.
Le circuit est alimenté par un générateur de force électromotrice E. Le condensateur est initialement non chargé. On suppose que t = RC = L/R. On ferme l'interrupteur K à l'instant t=0.

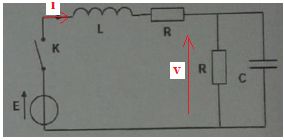
1. L'équation différentielle vérifiée par l'intensité i(t) s'écrit :
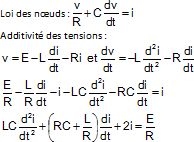Réponse A.
2. L'intensité du courant dans le circuit varie selon la relation :
Réponse A.
Réponse d'un cirduit RC.
Le générateur de tension délivre des signaux e(t) en crénaux d'amplitude E, de valeur moyenne nulle et de période T.

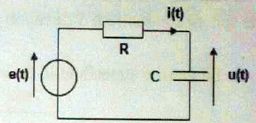
3. Les tensions maximale u_max et minimales u_min aux bornes du condensateur sont :.

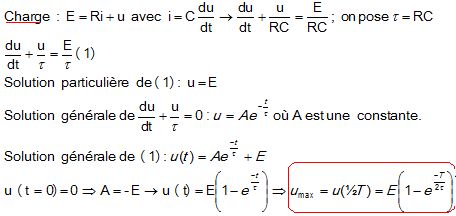
Lorsque ½T est supérieur à 5 t, u_max tend vers +E.
Lors de la décharge, la réponse A propose : u_min = -E(1-e^{-T / (2t)}) / (1+e^{-T / (2t)})
Lorsque ½T est supérieur à 5 t, u_mini tend vers -E. La réponse A convient.

Les conducteurs.
Une sphère conductrice S de rayon R est portée au potentiel V.
4. La densité superficielle de cette sphère est :
charge (coulomb) = surface sphère (m²) fois densité superficielle(Cm^-2)
Q=4pR²s.
potentiel V = Q / (4pe₀R) = Rs /e_{0 ;}s = Ve₀ /R. Réponse C.
5. On applique sur la partie haute de la sphère un petit disque métallique de masse m, de rayon r et d'épaisseur négligeable. Le potentiel auquel il faut porter la sphère pour que le disque se soulève est :
A l'intérieur d'un conducteur en équilibre le champ est nul.
A la surface d'un conducteur en équilibre le champ vaut s/e₀.
Au voisinage, à l'extérieur de la surface d'un conducteur , le champ E est normale à la surface, a pour valeur s/e₀. Il est dirigé vers la surface si les charges sont négatives et vers l'extérieur si elles sont positives.
Le disque prend une charge de densité s (charge disque q = s pr² )au contact de la sphère. Ce disque est soumis à une force F colinéaire au champ et de même sens, de valeur
qE= s² pr²/(2e₀) avec s= Ve₀/R.
F = e₀pr² V²/(2R²)
Le disque se soulève dés que cette force est supérieure au poids du disque( mg).
d'où la valeur limite de V : V²= 2mgR² / (e₀pr²). Réponse B.

.
.

6. La sphère est portée au potentiel V₁ > V, le disque atteint une position d'équilibre à une hauteur z au dessus de la sphère. La hauteur z s'exprime par :
Le disque se soulève d'une hauteur z au dessus de la sphère emportant la charge s pr².
Compte tenu des dimensions du disque, la charge de la sphère n'est guère modifiée. La sphère crée à cette hauteur z un champ E de valeur
E= 1/ (4pe₀) Q/(R+z)²= RV₁ / (R+z)²Le disque atteind une position d'équilibre lorsque la force électrique s pr²E est égal au poids du disque.
s pr²RV₁ / (R+z)²= mg avec s= V₁e₀/R
(R+z)²= pe₀V₁²r² /(mg) = 2R²V₁² / V².
R+z= 2^½RV₁/V ; z = R(2^½V₁/V -1). Réponse A.

Champ créé par un fil.
On considère un fil isolant rectiligne supposé infini uniformément chargé ( charge l par unité de longueur).
7. Le champ électrique créé par le fil en un point I du plan médiateur situé à une distance "a" du fil est :
On exprime les champs élémentaires créés par les éléments dl et dl' symétriques du point O.
Les composantes axiales de ces champs s'annulent ; les composantes radiales s'ajoutent.
Réponse D.

Déplacement sur rail de Laplace.
Une barre MN se déplace à vitesse constante v sur deux barres conductrices parallèles supposées infinies distante de d. Le galvanomètre de résistance R est à l'abscisse x=0 et la résistance des barres est r ( W m^-1 ). L'ensemble est placé dans un champ B uniforme. La barre reste normale à l'axe.
8. L'intensité du courant dans le galvanomètre est :
Par ses effets électromagnétiques, le courant induit engendre une force de freinage ( Loi de Lenz ).
Longueur du circuit à la date t=0 : 2x₀+d ; à la date t : 2(x₀-vt) +d.
Résistance totale ( circuit + galvanomètre) : 2(x₀-vt)r +dr +R.

Coefficient de self-induction.
On considère deux fils conducteurs distincts, rectilignes et parallèles ayant chacun un rayon r. Les axes des deux fils sont distants d'une distance d et traversés par deux courants constants de sens contraire et de même intensité I.
9. Le coefficient de self-induction par unité de longueur est :

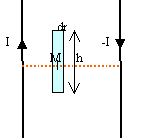
Champ crée par les 2 conducteurs en M : B=µ₀I / (2px) + µ₀I / (2p(d-x)).
Flux de B à travers une bande de largeur dx et de hauteur h paralèlle aux fils :
dF = B h dx =µ₀Ih / (2p)[ dx/x + dx/(d-x)]
En intégrant entre r et d-r : F =µ₀h / p ln((d-r)/r) I
Inductance L=µ₀ / p ln((d-r)/r) par unité de longueur. Réponse C.

Détermination du coefficient d'induction mutuelle.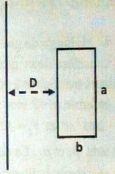
Un cadre rectangulaire de cotés vertical a et horizontal b et de résistance R comporte N spires. Ce cadre est placé au voisinage d'un fil conducteur vertical, très long, parcouru par un courant d'intensité I. Le cadre et le fil se trouvent dans le même plan. La distance du fil au cadre est D.
10. Si le courant d'intensité I est continu, le coefficient d'induction mutuelle fil-cadre est :
Champ crée par le conducteur à la distance x : B=µ₀I / (2px).
Flux de B à travers une bande de largeur dx et de hauteur a: dF = B adx =µ₀IN adx / (2px).
Intégrer entre D et D+b : F = µ₀I Na / (2p) ln((D+b) / D).
M = µ₀ Na / (2p) ln(1+b / D). Réponse B.

11. Si le courant dans le fil est alternatif sinusoïdal d'intensité i = I_m sin (wt), l'intensité du courant induit vérifie la relation :
Fem induite dans le cadre : e = -dF/dt = -MwI_m cos (wt).
Si on néglige l'inductance L du cadre : e = Ri ; MwI_m cos (wt)+ Ri =0. Réponse A.
Si on tient compte de l'inductance L du cadre : e = Ri+Ldi/dt ; MwI_m cos (wt)+ Ri +Ldi/dt =0. Réponse D.

.

menu