Satellite,
mouvement d'un cerceau.
Concours ENS 2015.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
A1. On
s'intéresse à la mise en place sur une orbite circulaire équatoriale
d'altitude h = 200 km d'un satellite de masse m=4200 kg. Initialement
le satellite est sur la base de lancement au niveau de la mer, au
voisinage de l'équateur.
On étudie le mouvement du satellite dans le référentiel géocentrique,
supposé galiléen. R = 6400 km ; M = 6,0 1024 kg ; G = 6,67 10-11
N m2 kg-2.
1. La vitesse v du satellite sur
l'orbite circulaire est :
v2 = GM/r = GM((R+h) ; v = [GM
/ (R+h)]½.
v = [6,67
10-11 *6,0 1024 / / ((6400+200) 103)]½=7,79
103 m /s ~7,8 km /s.
Réponse B.
2.
La période T du satellite sur son orbite est :
Le satellite décrit la circonférence 2p(R+h) à la vitesse v en T
secondes.
v = 2p(R+h)
/ T ; T = 2p(R+h)
/ v =6,28 *6600 / 7,79 =5,32 103 s= 1 h 29 min. Réponse B.
3.
La variation d'énergie mécanique du satellite entre sa position au sol
et son orbite d'altitude h est : ( on choisit l'origine de l'énergie
potentielle de pesanteur à l'infini ).
L'énergie mécanique initiale est égale à EM init= -GMm / R.
L'énergie mécanique finale vaut : EM final= ½mv2 -MGm /(R+h) =½m MG /
(R+h) -MGm /(R+h)
EM
final= -½m MG / (R+h).
DEM= -½m MG / (R+h) +GMm
/ R= GMm [1 /R -1/(2(R+h)) ].
4. Dans cette question, on tient
compte des frottements. Leur influence fait que :
L'énergie mécanique du satellite freiné par
l’atmosphère diminue du travail des frottements.
Or
E= -Ec=-½mv2 ; si E diminue alors la vitesse du
satellite augmente.
Or
E=-½Ep = -½mGM/( R+h) ; si E diminue alors la distance h
diminue.
Réponse B.
|
| .
. |
|
|
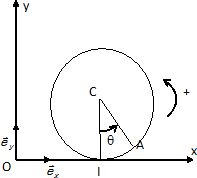
A2. Un
cerceau homogène de masse m, de centre C et de rayon a roule sans
glisser sur l'axe Ox d'un repère galiléen. Le cerceau est astreint à se
déplacer dans le plan vertical yOx.
On
désigne par I le point de contact du cerceau avec le sol, par A un
point fixe du cerceau, par x l'abscisse instantanée de C. A l'instant
t=0, x=0 et q=0.
5. La relation
entre x et q est
: x = -a q
avec q en radian. Réponse A.
6. En utilisant le
théorème de Koenig, l'énergie cinétique du cerceau dans le repère R est
:
Ec =½m v2+½J w2 = ½m x'2
+½ma2q'2.
Le roulement s'effectue sans glissement et q' =x' / a :
Ec
=½m x'2
+ ½mx'2 = mx'2. Réponse B.
7. L'expression de
la vitesse vA du point A dans R, exprimée dans le repère xOy
est :
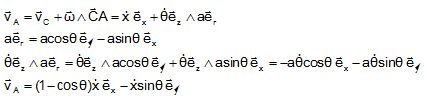 Réponse A. Réponse A.
8.
Un lest ponctuel de masse M est soudé au point A du cerceau. L'énergie
cinétique dans R du cerceau ainsi lesté est :
L'énergie cinétique du cerceau lesté est égale à l'énergie cinétique du
cerceau augmentée de l'énergie
cinétique du lest.
Ec = mx'2 +½MvA2 =mx'2
+½M [(1-cosq)2x'2 +sinq2x'2 ]
Ec
=mx'2
+M[(1-cosq)x'2. Réponse C.
|
|
|
|
9. L'expression de la puissance P
dans R du poids du lest est :.
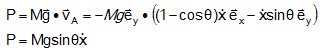 Réponse D. Réponse D.
10. On étudie les petit mouvement du
cerceau lesté autour de sa position d'équilibre. On montre que pour q <<1, l'équation
différentielle à laquelle obéit l'abscisse x du cerceau s'écrit : x" +w0x=0.
L'expression de w0
est :
Seul le poids du lest a une puissance non nulle. Le théorème de la
puissance cinétique appliquée au cerceau lesté dans R s'écrit :
dEc/dt = P.
2mx'x"+2M(1-cosq)x'x"
= Mgsinqx'.
2mx"+2M(1-cosq)x" = Mgsinq.
On étudie les petites oscillations autour de la position d'équilibre
stable qéq
= -xéq /a.
On linéarise l'équation différentielle au voisinage de la position
d'équilibre, au premier ordre :
2mx" =Mg q
avec x= -aq.
2mx" +Mg x / a=0.
2max"+Mgx =0 ; w02
= Mg / (2ma). Réponse C.
|
|
|
|