QCM Optique,
points de Bravais. Concours CPR 2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
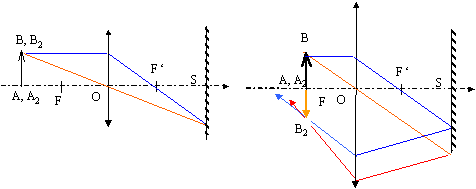
Système optique.
Un système optique est constitué par :
- une lentille convergente L, de centre O, de distance focale f. F et
F' sont les foyers de L ;
- un miroir plan centré en S sur l'axe Oz de la lentille, et disposé
parallèlement à celle-ci à la distance d = 2 f.
Un objet réel est disposé perpendiculairement à l'axe optique dans une
position telle que p = distance algébrique de OA. Soit A1B1
son image après traversée de L et réflexion sur M.
17. La position de
l'image A1B1 s'exprime par :
Soit A'B' l'image de AB
à travers la lentille L. La formule de conjugaison de Descartes donne :
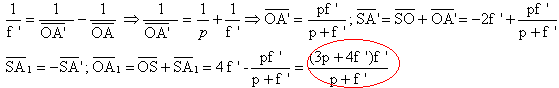
A1B1
est l'image de AB' dans le miroir ;
A1B1 est symétrique de AB' par rapport au plan du
miroir et en conséquent SA1
= -SA'.
Réponse B.
.
18.
Soit A2B2 l'image définitive après retraversée de
la lentille. La position p2 de cette image s'exprime par :
La seconde traversée de la lentille se
fait dans le sens contraire de l'axe Oz : donc le foyer image est
maintenant F. La formule de Descartes s'écrit alors ( A1B1
objet et A2B2 image) :
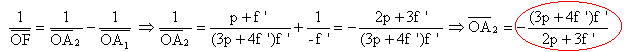
Réponse B.
|
| .
. |
|
|
19.
La condition à laquelle doit satisfaire p pour que AB et A2B2
soient dans le même plan ( correspondant à deux points de l'axe dit
points de Bravais ) est :
A est au point de Bravais si
OA2 = p
p(2p+3f ') = -(3p+4f ') f ' ;
2p² +3pf ' + 3pf ' +4f '² =0
p² + 3 f ' p + 2 f '² = 0
p doit être solution de l'équation du second degré ci-dessus
p1 = -2 f ' et p2
= - f '.
Réponse A.
|
|
|
|
20. Le grandissement g transversal du système est
:
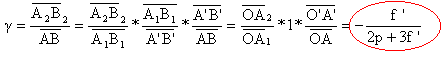
dans les positions de
Bravais, ce grandissement vaut g
1 = 1 et g 2 = -1.
Réponse D.
|
|
|
|