Les modèles primitifs de l'atome ; laser et rétine. Second concours, école normale supérieure 2015 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . 1. le modèle de Rutherford Rutherford décrit l'atome d'hydrogène selon le lodèle planétaire : l'électron de masse m est en mouvement circulaire autour du noyau réduit à un proton. La force subie par l'électron est radiale attractive, de valeur F = e2 /(4pe0r2). On négligera la force gravitationnelle devant la force électrostatique. 1.1- Faire un schéma de la situation. 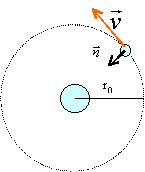1.2- Démontrer que le mouvement de l'électron est uniforme. La force électrostatique, perpendiculaire à la vitesse, ne travaille pas. D'après le théorème de l'énergie cinétique, l'énergie cinétique de l'électron n'est pas modifiée. La valeur de la vitesse de cet électron est donc constante. Le mouvement est uniforme. 1.3- Etablir l'expression de la vitesse v en fonction de e0, e, r et m. 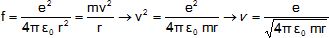1.4- En déduire son énergie cinétique Ec. Ec = ½mv2 =0,5 e2 /(4pe0r). 1.5- L'énergie potentielle de l'électron est : Ep = - e2 /(4pe0r). Exprimer son énergie mécanique Em en fonction de e0, e et r . Em = Ec +Ep = 0,5 e2 /(4pe0r)- e2 /(4pe0r) = -0,5 e2 /(4pe0r). 1.6- Que vaut son énergie mécanique lorsque r tend vers l'infini ? Commenter. L'énergie mécanique de l'électron tend vers zéro si r tend vers l'infini. L'électron est libre, il n'est plus lié à l'atome. 1.7- Le modèle de Rutherford est-il satisfaisant ? Pourquoi ? Ce modèle n'est pas satisfaisant. L'électron rayonne de l'énergie, son énergie mécanique diminue et il va finir par s'écraser sur le proton. Ce modèle ne rend pas compte de la quantification de l'énergie. 2. Le modèle de Bohr. Bohr formule l'hypothèse que l'électron ne peut se déplacer que sur certains cercles de rayon rn. Ces rayons sont tels que le produit m vn rn, appelé moment cinétique de l'électron vérifie la loi : m vn rn= n h /(2p). n est un nombre entier, h la constante de Plank, vn la vitesse de l'électron sur le cercle de rayon rn. 2.1- Si le modèle planétaire de Rutherford était valide, comment devrait être le spectre d'émission de l'hydrogène ? Dans ce modèle, l'énergie de l'électron n'est pas quantifié. Le spectre d'émission de l'hydrogène serait continu et non pas discontinu. 2.2- Pourquoi parle t-on de quantification du moment cinétique dans le modèle de Bohr ? Toutes les valeurs ne sont pas possibles, seules un petit nombre est permis. h /(2p), 2 h /(2p), 3 h /(2p)..... . . 2.3- Déterminer l'expression de rn en fonction des constantes e0, h, m, e et n. 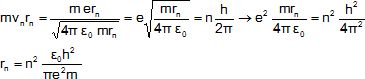2.4- Exprimer rn en fonction de r1 et calculer r1. 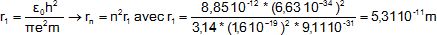2.5- Montrer que l'énergie mécanique de l'électron sur le cercle de rayon rn peut se mettre sous la forme En = -E0 / n2. 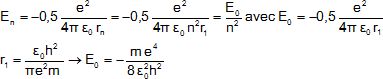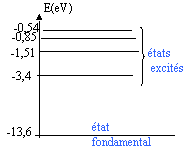2.6- Calculer E1, E2, E3 en (eV) et représenter ces trois niveaux sur un diagramme énergétique. E0= -9,11 10-31*(1,6 10-19)4 / (8*(8,85 10-12 )2*(6,63 10-34)2)= -2,17 10-18 J. -2,17 10-18 /(1,6 10-19)~ -13,6 eV. E1 = -13,6 eV ; E2 = E0/4 = -3,38 eV ; E3 = E0/9 = -1,51 eV.; 3- Pour aller plus loin. Le modèle fut appliqué à l'étude des hydrogénoïdes ( He+ ; Li2+ ; Be3+...). On note Z le numéro atomique de l'hydrogénoïde étudié, c'est à dire le nombre de protons présents dans le noyau. 3.1- Quelle est la particularité d'un ion hydrogénoïde ? Un ion hydrogénoïde posséde un électron et Z protons : il a la même structure électronique que l'atome d'hydrogène. 3.2- Exprimer la force électrostatique et l'énergie potentielle de l'électron de l'hydrogénoïde. F = Ze2 /(4pe0r2). Ep = = - Ze2 /(4pe0r) 3.3- Comparer les valeurs des niveaux d'énergie d'un hydrogénoïde de numéro atomique Z à celles des niveaux d'énergie de l'atome d'hydrogène. On remplace e2 par Ze2 dans les expressions ci-dessus : En = E0 (Z / n)2. 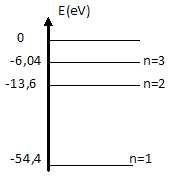3.4- Représenter les trois niveaux d'énergie pour l'hydrogénoïde He+( Z=2). Comparer à l'atome d'hydrogène. Commenter. E'1 = 4E0 = -4*13,6 = -54,4 eV. E'2 = E0 =  -13,6 eV. E'3 = E0 (2 / 3)2. = -2*1,51 = -6,04 eV. Ces énergies sont, en valeurs absolues, quatre fois plus grandes que les énergies correspondantes de l'atome d'hydrogène. Laser et rétine. Le laser à ions d'argon émet dans le vert à une longueur d'onde l = 514,5 nm avec une puissance P = 0,50 W. L'angle de divergence du faisceau est W = 5,2 mrad. A sa sortie, le faisceau a un diamètre D = 200 µm. 4.1- Citer deux caractéristiques d'un laser. Faicesau de lumière pratiquement monochromatique, très directif, transportant une grande énergie par unité de surface. 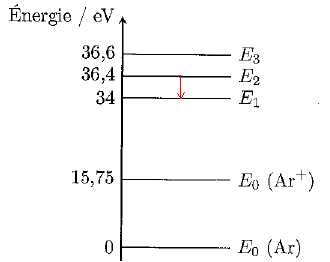4.2- Quelle est la variation d'énergie correspondant à l'émission de la raie verte du laser ? E = h c /l =6,63 10-34*3,00 108 / (514,5 10-9)=3,86 10-19 J ~2,42 eV. 4.3- Indiquer la transition correspondante sur le diagramme d'énergie. 4.4- Le faisceau est-il détectable par un observateur placé latéralement à l'axe du faisceau ? Oui, si l'air contient de fines particules en suspension ; non, dans le cas contraire. 4.5- Quel est le diamètre du faisceau à la distance d = 50 cm ? Dans l'approximation des petits angles : 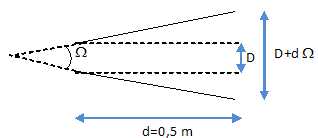200 10-6 +0,5 *5,2 10-3 = 2,8 10-3 m =2,8 mm. 4.6- Accidentellement, l'oeil de l'expérimentateur se trouve dans l'axe du faisceau à 50 cm de la source. Ce faisceau entre-t-il entièrerment dans la pupille ? Le diamètre de la pupille est supérieur à 3 mm. Le faisceau pénètre entiérement dans la pupille. 4.7- L'oeil peut être modélisé par une lentille mince de distance focale f = 17 mm. Calculer le diamètre du D" de la tache lumineuse sur la rétine. La source lumineuse peut être considérée à l'infini ( 17 mm << 50 cm). Le diamètre apparent de cette source est voisin de : a=200 10-6 / 0,5 = 4 10-4 rad. L'image de cette source se forme sur la rétine : D" ~ a f = 4 10-4 *0,017 =6,8 10-6 m. 4.8- Evaluer l'intensité lumineuse de cette tache. Surface de la tache circulaire sur la rétine : pD"2/4=3,14 *(6,8 10-6)2/4 ~3,6 10-11 m2. Intensité lumineuse (Wm-2) = Puissance ( W) / surface (m2)=0,50 / (3,6 10-11)=1,4 1010 W m-2. 4.9- Par comparaison, l'intensité de la lumière solaire est Is = 1000 W m-2. Commenter. La lumière laser est très dangereuse pour l'oeil. .

menu