Chute d'une balle, transferts thermiques. Concours Adjoint Technique Principal de recherche et de Formation Toulon 2013 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Chute libre d'une balle de golf d'une hauteur de 1,80 m. Masse de la balle : m = 45,0 g ;volume de la balle : V = 58,2 mL ; valeur de la pesanteur lunaire : 1,65 SI. 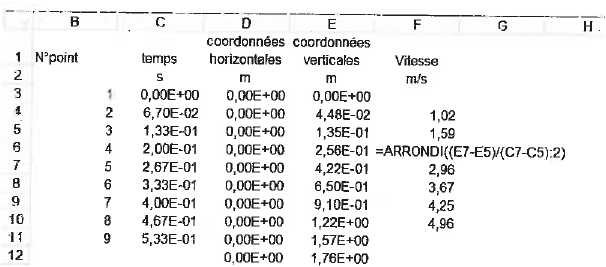Donner le nom d'un logiciel de pointage vidéo.Regressi et Regavi Donner l'intervalle de temps séparant deux positions successives de la balle. 0,067 s = 67 ms. En vous aidant de la formule donnée dans la cellule F6, calculer la valeur de la vitesse que doit afficher cette cellule. La fonction ARRONDI(nombre2) affiche le nombre avec un arrondi à deux chiffres après la virgule. =ARRONDI((0,422-0,135) / (0,267-0,133) :2))=2,14 m/s. 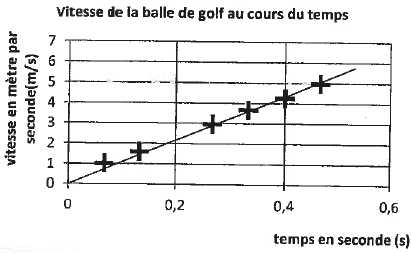Définir le mouvement de la balle dans le référentiel terrestre et donner la relation entre vitesse et temps. La vitesse est une fonction linéaire du temps. La chute est uniformément accélérée. v = k t avec k = 9,81 m s-2 sur la terre ou 1,65 ms-2 sur la lune. Dans l'hypothèse d'une vitesse initiale nulle v = (2gh)½. Retrouver ce résultat à l'aide du théorème de l'énergie cinétique. Variation d'énergie cinétique : ½mv2-0 ; seul le poids travaille ( chute libre ) : travail dupoids mgh. ½mv2=mgh soit v2 = 2gh. Calculer la vitesse de la balle si h = 1,8 m. v =(2*9,81*1,8)½=5,9 m/s. Si la hauteur de chute libre est quadruplée, par combien est multipliée la vitesse? La vitesse est proportionnelle à la racine carrée de la hauteur. La vitesse double. Dans cet exercice la balle est soumise à trois forces : son poids, la poussée d'Archimède et les forces de frottement exercées par l'air. Calculer le poids de la balle sur  terre. P = mg = 0,0450*9,81 =0,441 N. La poussée d'Archimède est proportionnelle au volume de la balle. Masse volumique de l'air r=1,20 g/L= 1,2 kg m-3. Calculer la valeur de la poussée. F =Vgr =58,2 10-6*1,2*9,81 =6,85 10-4 N. . . La force de frottement est proportionnelle au carré de la vitesse. Par combien environ sont multipliées les forces de frottement lorsque la balle passe de la position 2 à la position 8. La vitesse passe de 1,02 m/s à 4,96 m/s. La vitesse étant multipliée par environ 5, la valeur des forces de frottement est multipliée par environ 25. Lorsque la hauteur de chute devient importante, le principe d'inertie prévoit que la bille atteigne une vitesse limite. Vlim = 31,1m/s. Enoncer le principe d'inertie. Dans un référentiel galiléen, le centre d'inertie d'un système pseudo-isolé est soit au repos soit animé d'un mouvement rectiligne uniforme. Convertir la vitesse limite en km/h. 31,1 *3,6 ~112 km/h. Calculer l'énergie cinétique de la balle lorsqu'elle atteint sa vitesse limite. ½mv2 =0,5*0,045*31,12 ~21,8 J. . Transferts thermiques. On utilise un chauffe-ballon contenant un ballon avec 300 g d'eau. La puissance annoncée par le constructeur de ce chaufe-ballon est P=200 W. L'élément chauffant est un conducteur ohmique purement résistif. Lorsque l'appareil est en fonctionnement, on utilise un compteur électrique muni d'un disque qui tourne pour mesurer l'énergie électrique consommée. C =2,5 Wh /tour indique la quantité d'énergie consommée en Wh lorsque le disque effectue un tour. On branche le chauffe-ballon à la sortie du compteur. Le compteur effectue exactement 10 tours en un temps t = 7 minutes et 19 secondes. Calculer en joules l'énergie consommée par le chauffe-ballon. W=2,5 *10 = 25 Wh ou 25*3600 = 9,0 104 J = 90 kJ. Calculer en watts la puissance réelle P' du chauffe-ballon. P' = W / Dt = 9,0 104 / ((7*60+19)=205 W. On mesure la température de l'eau à l'aide d'un thermomètre. Calculer l'élévation maximale de la température de l'eau. Ceau = 4180 J kg-1 K-1. W = m ceau Dq ; Dq = W /(m ceau) = 9,0 104 /(0,3*4180) = 7,8 ~78°C. .

menu