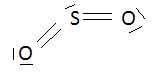Autour du dioxyde
de soufre : procédé Bayer, dosage du dioxyde de soufre dans un vin
blanc. Concours DGCCRF 2015
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
Etude
de la molécule.
Représenter le schéma de lewis de la molécule de dioxyde de soufre.
Indiquer sa géométrie. Type
AX2E.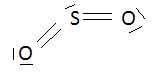
Obtention
industrielle.
Un
des procédés industriels d'obtention du dioxyde de soufre consiste à
réaliser la combustion du soufre dans le dioxygène de l'air dans un
four.
S(s) + O2(g) --> SO2(g)
DrH(298
K) ~-300 kJ mol-1.
Un
mélange constitué d'une mole de soufre, de deux moles de dioxygène et
de huit moles de diazote est introduit à 298 K dans un four. Faire le
bilan des espèces en fin de réaction en considérant celle-ci comme
totale.
Une mole de
dioxyde de soufre, une mole de dioxygène et huit moles de diazote.
Calculer l'énergie libérée par cette réaction chimique.
Cette
réaction libère 300 kJ par mole de dioxyde de soufre formé.
Calculer
la température des gaz à la sortie du four après combustion effectuée
sous une pression constante de 1,00 bar, en admettant que le système
gazeux évolue de manière adiabatique.
3,00 105 = (Cp,m(O2) +Cp, m(SO2) +8Cp, m(N2)) Dq.
3,00 105 =
(34,24 +51,10 +8*30,65) Dq ; Dq ~908°C.
Température
des gaz : 298+908 ~1,2
103 K.
Procédé
Bayer.
On
étudie l'équilibre suivant dans un domaine de température où tous les
composés sont gazeux et assimilés à des gaz parfaits : 2SO2(g)
+O2(g) = 2SO3(g).
Calculer
l'enthalpie et l'entropie standard de réaction à 298 K.
Commenter
les signes et indiquer l'influence de l'augmentation de la température
à pression constante sur un tel équilibre.
|
O2(g)
|
SO2(g)
|
SO3(g)
|
|
DfH°298
( KJ/mol)
|
0
|
-296,8
|
-395,7
|
|
S°298 ( J K-1
mol-1)
|
205,0
|
248,1
|
256,6
|
L’approximation
d’Ellingham consiste à supposer que DrH° et DrS° sont indépendantes de la
température en dehors des changements d’état.
DrH =2 DfH°298 (SO3(g) -2 DfH°298 (SO2(g))-DfH°298(O2(g))
DrH = 2(-395,7 -(-296,8)) = -197,8 kJ/mol.
DrH négative : réaction
exothermique favorisée par une diminution de la température à pression
constante.
DrS = 2S°298 (SO3(g) - 2S°298 (SO2(g))- S°298(O2(g))
DrS =2*256,6-2*248,1-205,0 = -188 J K-1
mol-1.
DrS négative : le nombre de
molécules final est inférieure au nombre de molécules initial.
Donner
l'expression de l'enthalpie libre standard de réaction en fonction de
la température T. En déduire l'expression de la constante
thermodynamique d'équilibre.
DrG =
DfH
-T DrS.
DrG = -197,8 103 +188,0 T = -RTln
K°.
lnK° =197,8 103 / (8,314 T)- 188 /8,314.
lnK° = 2,379
104 / T -22,61.
|
.
.
|
|
|
Retrouver
l'influence sur l'augmentation de température à pression constante sur
l'équilibre étudié.
Si la température diminue, à pression constante, ln K augmente,
l'équilibre est déplacé dans le sens direct.
Quelle est l'influence de la pression totale à
température constante sur l'équilibre ?
Le
nombre de moles final est inférieur au nombre de moles initial. Une
augmentation de pression, à température constante, déplace l'équilibre
dans le sens direct.
On travaille dans cette question à
pression constante notée P. L'équilibre est obtenu à partir d'un
mélange stoechiométrique de dioxyde de soufre et de dioxygène. On note a le
taux de dissociation du dioxyde de soufre et n0
la quantité initiale de dioxygène. Indiquer l'expression de K
en
fonction des pressions partielles des différents constituants puis en
fonction de a,
P et P0, pression standard.
K = P2SO3 P0/ (PO2 P2SO2).
a =2x
/(2n0) = x/n0.
|
avancement
(mol) |
2SO2(g) |
+O2(g) |
=2SO3(g) |
| initial |
0 |
2n0 |
n0 |
0 |
| à
l'équilibre |
x |
2n0-2x=2n0(1-a) |
n0-x=n0(1-a) |
2x= 2n0a |
Nombre total de mole à
l'équilibre :3n0-x = n0(3-a).
Pressions partielle des gaz : PSO3
=2x/(3n0-x) P =2a/(3-a)P ;
PO2 =(n0-x) /(3n0-x) P =(1-a) / (3-a)P ; PSO2 =(2n0-2x)/(3n0-x) P =2(1-a) / (3-a)P.
K = 4a2 (3-a)P0/
(4(1-a)3P) = a2 (3-a)P0/((1-a)3P) .
A quelle pression
doit-on travailler si on souhaite obtenir un taux de dissociation de 98
% à la température de 450 °C ?
P0 = 1 bar ; T = 450+273 =723 K ;
ln K = 2,379 104 / 723 -22,61 = 10,2945 ; K =
2,957 104.
2,957 104 =0,982(3-0,98)
/(1-0,98)3 P).
2,957 104 =1,94 / (8 10-6
P) ; P = 8,2
bar. |
.
|
|
Dosage du dioxyde de soufre dans un vin blanc.
Le SO2
est peut être la seule substance indispensable dans les chais de
vinification. Lors de l'incorporation de l'anhydride sulfureux SO2,
dans un moût ou un vin, une fraction de celui-ci va se combiner aux
sucres, ou plus généralement aux aldehydes ( éthanal ) présents
dans le vin.
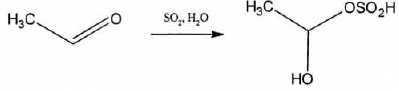
On peut utiliser la méthode de Ripper. La forme libre de SO2
est dosée en milieu acide par titrage iodométrique direct et la forme
combinée par la différence entre l'anhydride sulfureux total et
l'anhydride sulfureux libre. Le SO2 combiné est hydrolysé en milieu basique : en effet, en milieu basique, le SO2
combiné est libéré sous forme de sulfite de sodium. En présence d'acide
sulfurique ( 5 mL à 5 mol/L ), celui-ci permet de régénérer le dioxyde
de soufre.
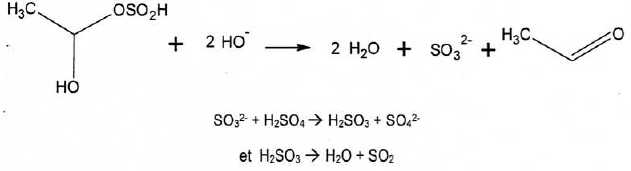
Le dioxyde de soufre total est alors dosé par une solution de diiode à 4,00 10-3 mol/L en présence d'un indicateur coloré.
Ecrire l'équation de dosage associé à la méthode de Ripper et calculer sa constante thermodynamique d'équilibre.
E°(SO42-/SO2) = 0,17 V ; E°(I2/I-) =0,54 V.
SO2 +2H2O= SO42- + 2e- +4H+. E°1 = E°(SO42-/SO2) +0,03 log( [SO42-][H+]4/[SO2] )
I2 + 2e- = 2I- ; E°2 = E°(I2/I-) +0,03 log ([I2]/[I-]2).
SO2 +2H2O +I2= SO42- + 2I- +4H+. K = [SO42-][H+]4/[I-]2 / ([SO2][I2] ).
A l'quilibre E°1 = E°2 ; E°(SO42-/SO2) +0,03 log( [SO42-][H+]4/[SO2] ) =E°(I2/I-) +0,03 log ([I2]/[I-]2).
E°(I2/I-) - E°(SO42-/SO2) =0,03 log( [SO42-][H+]4/[SO2] )-0,03 log ([I2]/[I-]2) = 0,03 log K.
log K = (0,54-0,17) / 0,03 = 12,3 ; K = 2,15 1012 ~2,2 1012.
On dose une prise d'essai de E = 25,00 mL d'un vin blanc par la méthode
de Ripper, après avoir libéré le dioxyde de soufre combiné. Volume à
l'équivalence V= 7,80 mL.
Proposer un indicateur coloré permettant de détecter l'équivalence de ce dosage. Préciser les changements de couleur observés.
La seule espèce colorée est le diiode ; ce dernier forme avec l'empois d'amidon
un complexe de teinte violet foncé.
Avant l'équivalence le diiode est en
défaut, après l'équivalence, il est en excès. A l'équivalence, la teinte de la
solution passe du vert très pale au violet foncé.
Calculer la teneur totale en dioxyde de soufre de ce vin en mg/L et conclure.
A l'équivalence : quantité de matière de diiode n(I2) =7,80 10-3 *4,00 10-3 = 3,12 10-5 mol.
Quantité de matière de dioxyde de soufre : n(SO2) = n(I2) =3,12 10-5 mol dans 25,00 mL de vin blanc.
[SO2]=3,12 10-5 /0,0250 =1,248 10-3 mol/L soit : [SO2] M(SO2) =1,248 10-3 *64=7,99 10-2 g/L = 79,9 mg/L.
Cette valeur étant inférieure à 150 mg/L, le vin blanc est conforme à la norme.
|
|
|