Saut
à ski, équilibre d'une échelle, électricité. Concours
Ecole
Nationale Supérieure Maritime 2015
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
Tremplin
de saut à ski.
Un
champion de saut à ski, assimilable à un corps ponctuel S, s'élance
d'un point A avec une vitesse initiale nulle sur une piste de saut.
Masse du skieur m = 70 kg.
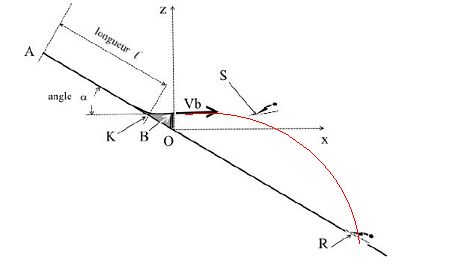
Du point A au point K, la piste est considérée comme rectiligne, puis
elle se termine par un tremplin horizontal qui s'achève au point B, à
la même altitude que le point K. La courbure entre le haut de la piste
et le tremplin est négligée, mais on considère qu'elle permet de
conserver la même vitesse entre les points K et B.
La piste de réception est le prolongement du haut de la piste et les
points A, K, O et R sont alignés sur une droite inclinée d'un angle a =
27° par rapport à l'horizontale.
Dans tout le problème, on néglige les frottements de l'air sur le
skieur et ceux des skis sur la piste.
On associe au référentiel terrestre le repère (Ox, Oz) ; le point O est
situé 6 mètres sous le point B et à sa verticale.
1.
Déterminer la distance l
entre les points A et K pour que la vitesse du skieur soit de 90 km.h-1
au point B.
Entre A et
K, l'énergie
mécanique se conserve. Pour cette question l'origine de l'énergie
potentielle de pesanteur est prise en K.
En A
l'énergie mécanique du skieur est sous forme potentielle : mg l sin a.
En K
l'énergie mécanique est sous forme cinétique ½mv2.
mg l sin a = ½mv2.
l = ½v2 / (g sin a) avec v = 90/3,6 = 25 m /s.
l =0,5*252
/(9,8 sin 27) =70,23 ~70 m.
2. Faire le bilan
des forces qui s'exercent sur le skieur à partir du point B et donner
les caractéristiques de ces forces.
Le skieur
est en chute libre Il est soumis uniquement à son poids, verticale
vers le bas, valeur mg = 70*9,8 =686 N.
3.
Etablir les équations horaires du point S dans l'air : x et z = f(t).
Dans le
repère proposé, accélération ( 0 ; -g).
Vitesse vx=vb ; vz= -gt.
Position x =
vbt ; z = -½gt2.
4.
Etablir l'équation cartésienne du point S dans l'air : z = f(x).
t = x / vb ; z = -½gx2 /v2b.
5.
En déduire la nature de la trajectoire du point S et la représenter
approximativement.
La
trajectoire est une branche de parabole.
6.
Etablir l'équation cartésienne de la droite représentant la piste de
réception OR.
z = - tan a
x = -tan 27 x = -0,5095 x~ -0,51
x.
7.
Le skieur se réceptionne au point R, calculer les coordonnées de ce
point.
-0,51 xR = -½gx2R / v2b.
xR = 2*0,51v2b / g =2*0,51 *252 /9,8 ~65 m.
zR = -0,51 *65 ~ -33 m.
8. Exposer sans
faire de calcul ce qui changera si le skieur prend de l'élan au départ
en poussant sur ses bâtons par exemple.
La vitesse
initiale sera plus grande ; donc vb et xR vont croître.
9.
De même, sans faire de calcul, exposer ce qui changera si le skieur
pousse sur ses jambes dans la dernière partie du tremplin.
vb et donc xR vont croître.
|
| .
. |
|
|
Equilibre
d'une échelle.
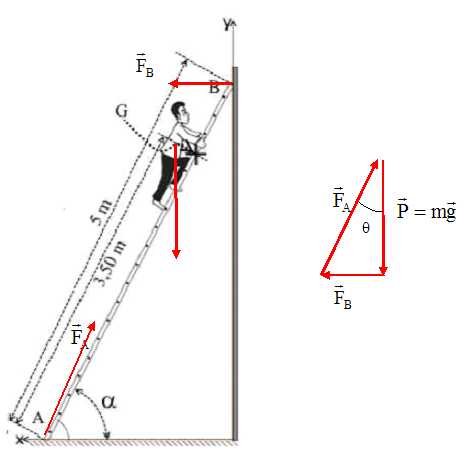
On considère un peintre qui monte sur une échelle reposant, en A, sur
un sol horizontal, avec un angle de 75° par rapport à l'horizontale, et
qui est appuyée contre un mur vertical, en B. Voir le schéma ci-dessous.
La masse de l’échelle est négligeable et sa longueur est de 5 mètres.
Le peintre a une masse de 80 kg et on considère que son centre de
gravité se situe sur l’échelle à 3,50 mètres du point A. Le mur et le
haut de l’échelle sont lisses, la réaction au point B est donc
perpendiculaire, ou normale, au mur.
Le sol et le bas de l’échelle ne sont pas lisses et on considère qu'il
y a un coefficient
de frottement, µS , égal à 0,20 ; ce qui
correspond à un angle q
de 11°.
On considère que l’échelle est en équilibre. Données : g = 10 N.kg-1
; a
= 75°.
1. Etablir le bilan
des forces s’appliquant sur l’échelle et les représenter sur un schéma.
L'échelle
est soumise au poids du peintre, à l'action du mur en B et à l'action
du sol en A.
2.
Calculer chacune de ces forces.
P = 80*10 = 8,0 102 N.
Moment de P
par rapport à un axe passant par A et perpendiculaire au plan de la
figure :
Bras de
levier : 3,5 cos 75 = 0,9058 m ; moment de P : 800 *0,9058
=724,7 Nm.
Le moment de
FA par rapport à cet axe
est nul.
Moment de FB par rapport à cet axe :
bras de
levier : 5 sin 75 = 4,83 Nm ; moment de FB : -4,83 FB.
A
l'équilibre la somme des moments est nulle : -4,83 FB + 724,7 =0 ; FB
=1,5 102
N.
FA = P / cos q =800 / 0,981 ~814 ~8,1 102
N.
3.
Vérifier que l’échelle tient en équilibre.
F2A =P2 +F2B =(8,02 +1,52 ) 104 ; FA ~8,1 102
N.
4.
Exposer ce qui se passerait si le peintre se déplaçait à 4 mètres du
point A.
Moment du
poids par rapport à l'axe :
Bras de levier : 4 cos 75 =
1,035 m ; moment de P : 800 *1,035 =828 Nm.
Le moment de
FA par rapport à cet axe
est nul.
Moment de FB par rapport à cet axe :
bras de
levier : 5 sin 75 = 4,83 Nm ; moment de FB : -4,83 FB.
Dans
l'hypothèse d'un équilibre, la somme des moments est nulle :
-4,83 FB + 828 =0 ; FB
=171 ~1,7 102 N.
FA restant inchangée : F2A diffère deP2 +F2B et l'équilibre est rompu.
L'échelle va glisser sur le mur et tomber.
|
|
|
|
Electricité.
. On considère le dipôle de la figure
ci-dessous.
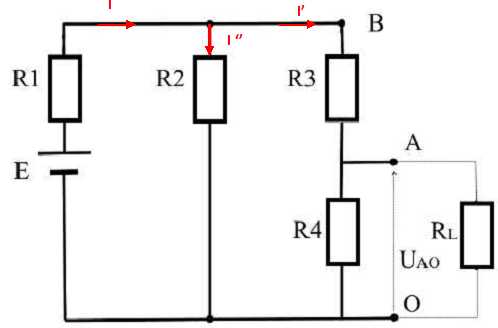
Données :E = 24 V ; R1 = 2 W ; R2 = 8 W ; R3 = 8 W ; R4 = 16 W ; RL = 6 W.
Pour les questions 1 à 3 incluse, la résistance de charge, RL, n'est
pas raccordée aux points O et A ; pour les questions 4 et 5, elle l'est.
1. Déterminer la tension à vide entre les points O et A, UAO.
Nota : on pourra calculer la tension UBO en considérant la résistance
équivalente entre R2, R3 et R4, puis étudier le diviseur de tension R3 / R4 ou bien
appliquer la loi des mailles et des noeuds ou toute autre méthode.
Résistance équivalente à R3 et R4 en série : R5 = R3+R4 = 8+16 = 24 W.
Résistance équivalente à R2 et R5 en dérivation : R6 = R2R5 /(R2+R5) =8*24 / 32 = 6 W.
Résistance équivalente à R1 et R6 en série : R7 = R1+R6 =2+6 = 8 W.
Intensité du courant principal I= E / R7 = 24 / 8 = 3 A.
Intensité du courant dans R5 : I' +I'' = I = 3 et UBO =8I''=24 I' ; I" = 3 I' ; I'=0,75 A
UAO = R4 I' =16*0,75 = 12 V.
2. Déterminer la résistance équivalente entre les points O et A si la
source de tension, E, est remplacée par un court-circuit.
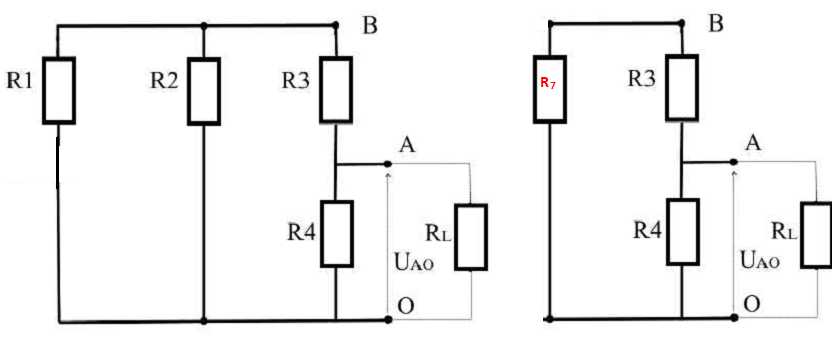
Résistance équivalente à R1 et R2 en dérivation : R7 = R1R2 /(R1+R2) =2*8 / 10 = 1,6 W.
Résistance équivalente à R7 et R3 en série : R8 = R7+ R3= 9,6 W.
Résistance équivalente à R4 et R8 en dérivation : RTh = R4R8 /(R4+R8) =16*9,6 / 25,6 ; RTh = 6 W.
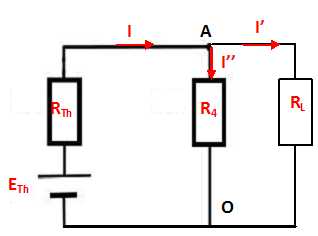
3. Représenter le modèle de Thévenin équivalent au dipôle OA.
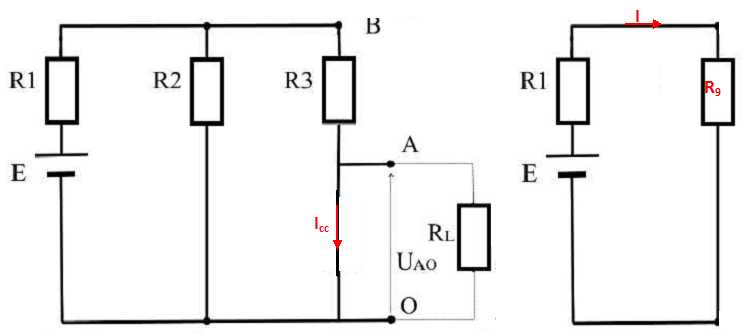
Résistance équivalente à R3 et R2 en dérivation : R9 = R3R2 /(R3+R2) =8*8 / 16 = 4 W.
Résistance équivalente à R1 et R9 en série : R10 = R1+ R9= 2+4=6 W.
Intensité principale I = E / R10 = 24 / 6 = 4 A.
Intensité du courant Icc : I2 +Icc= I = 4 et UBO =8I2=8 Icc ; I2 = Icc ; Icc = 2 A.
Fem du générateur de Thévenin Eth = Icc RTh=2*6 ; Eth =12 V.
4. On raccorde la résistance de charge RL aux bornes OA, calculer la
tension à ses bornes et le courant qui la traversera.
Résistance équivalente à R4 et RL en dérivation : R11 = R4RL /(R4+RL) =16*6 / 22 = 4,36 W.
Résistance équivalente à RTh et R11 en série : R12 = RTh+ R11= 6+4,36 =10,36 W.
Intensité principale I = ETh / R12 = 12 / 10,36 = 1,158 ~1,2 A.
Intensité du courant I' : I' +I''= I = 1,158 et UAO =16 I''=6 I' ; I" = 0,375 I' ; I' = 0,842 ~0,84 A.
UAO =RL I' = 6*0,84 =5,054 ~5,0 V.
5. Calculer la puissance dissipée dans la charge.
UAO I' =5,054 *0,842 ~4,3 W.
6. Calculer la puissance fournie par la source de tension, E.
Résistance équivalente à R4 et RL en dérivation : R13 = R4RL /(R4+RL) =16*6 / 22 = 4,36 W.
Résistance équivalente à R12 et R3 en série : R14 = R13+R3 =4,36+8 = 12,36 W.
Résistance équivalente à R2 et R14 en dérivation : R15 = R2R14 /(R14+R2) =8*12,36 / 20,36 = 4,86 W.
Résistance équivalente à R15 et R1 en série : R16 = R15+R1 =4,86+2 = 6,86 W.
Intensité du courant principal I= E / R16 = 24 / 6,86 = 3,5 A.
Puissance fournie par la source E : E I = 24 *3,5 ~84 W.
|
|
|
|