Gravitation.
Concours GEIPI 2015
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
|
|
|
|
Au cours d’une
émission télévisée matinale, un point route est effectué où
apparaissent plusieurs
écrans de contrôle de la situation routière, correspondants à
différents points du territoire.
Il est 8 heures du matin ce 20 octobre 2014 (293e
jour de l’année, N = 293) et le téléspectateur
constate qu’il fait nuit à Paris (latitude : 48,85° Nord, longitude :
2,35° Est) et jour à Nice, où le
soleil se lève (latitude : 43,70° Nord, longitude : 7,25° Est). Nous
vous proposons de vérifier cet
état de fait par le calcul en affectant l’indice 1 à Paris et l’indice
2 à Nice.
Le trajet du centre O de la terre autour du Soleil est une ellipse.
Quelle position le centre du Soleil occupe-t-il par rapport à cette
ellipse ?
Le centre du
soleil est un foyer de l'ellipse.
Pour simplifier, on fait maintenant l’hypothèse que cette trajectoire
est circulaire uniforme. La
vitesse V de O est alors constante, donnée par l’expression : v = (GM / r)½.
G
= 6,6700 10-11 m3.kg-1.s-2
est la constante de gravitation
M = 2,0059 1030 kg est la masse du soleil
r = 1,5000 1011 m est la distance Terre‐Soleil.
Calculer V en l’exprimant en m.s-1.
V = ( 6,6700
10-11*2,0059
1030
/(1,5000
1011) )½ =2,9866 104 m/s.
On considère donc que le centre de la terre O effectue un cercle autour
du Soleil. Quelle
est la distance d parcourue par la terre lors d’un tour complet ?
d = 2 p r = 2*3,14159 *1,5000 1011=9,4248 1011 m.
Déterminer l’expression littérale du temps T d’un tour complet (période
de révolution) en
fonction de p,
G, M et r. Calculer T en l’exprimant en secondes puis en jours.
2 p r = V T =(GM
/ r)½ T ; T = 2 p r1,5 / (GM )½
.
T = 2*3,14159 *(1,5000 1011)1,5
/ (6,6700
10-11*2,0059
1030)½ ;
T =3,15583 107 s =365,26 J .
Que
retrouve-t-on en exprimant le rapport T2/r3 ?
Comment se nomme la loi correspondante ?
On retrouve
la 3ème loi de Kepler T2/r3 = 4 p2/(GM).
La
durée du jour J en un point de la terre est donnée par l’expression (1)
où d
est la déclinaison
du soleil (angle fait par la direction Terre-Soleil dans le plan de
l’équateur terrestre) et f est
la
latitude du lieu.
J = 24(1-1/p arcos ( tan f tan d)) (1).
Pour d
= 0, calculer la durée du jour J0.
J0 =
24(1/3,14159 arcos 0) ; arcos 0 = 3,14159 / 2 =1,5708.
J0 =
24(1-1/3,14159 *1,5708) =12 heures.
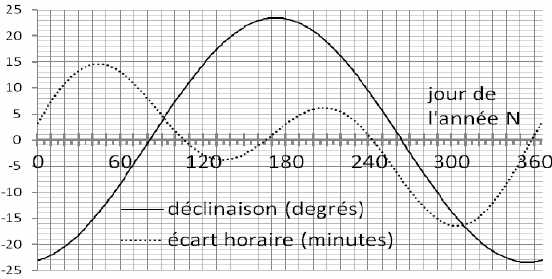
En
les relevant sur le graphique ci-dessous (en abscisse le numéro N du
jour, N = 1 correspondant au 1er janvier), donner les numéros des 2
jours correspondant de l’année. Comment appelle-t-on ces deux journées
particulières ?
Les équinoxes N
= 81 et N = 264.
Déterminer d
(à exprimer en degrés) pour le 20 octobre 2014 (N = 293) en le relevant
sur
le graphique. ~
-11,5 °.
|
| .
. |
|
|
Convertir en radian la déclinaison δ et les latitudes de Paris et Nice.
d = -11,5 *3,14159 / 180 =
-0,2007 rad.
f1 = 48,85 *3,14159 / 180 =
0,8526 rad.
f2 = 43,70 *3,14159 / 180 =
0,7627 rad.
Effectuer avec la formule (1) le
calcul des durées du jour à Paris et Nice ce 20 octobre,
soit J1 et J2, exprimées
en heures et minutes (l’équinoxe d’automne étant passée, la durée du
jour
est inférieure à 12h).
J1 = 24(1 -1/3,14159 arcos ( tan
0,8526 *tan(-0,2007)) =10,205
h. ( 10 h 12 min )
J2 = 24(1 -1/3,14159 arcos ( tan
0,7627 *tan(-0,2007)) =10,505
h.( 10 h 30 min)
En déduire l’heure
du lever du soleil ce jour là à Paris (notée HL1)
et Nice (notée HL2),
exprimées en heures et minutes : On a : HL = 12 h – J/2 . Ces résultats
correspondent à des
heures solaires exactes.
HL1=
12-10,205 / 2 ) ~6,90
h ou 6 h 54 min.
HL2=
12-10,505 / 2 ) ~6,75
h ou 6 h 45 min.
|
.
|
|
En tout point du territoire,
l’heure administrative de référence est la même, mais doit être corrigée
pour retrouver l’heure solaire locale exacte H. H est donnée, pour
chaque lieu, par la formule :
H = 6 +DHg-E(2)
DHg est la correction de
longitude. DHg s’obtient en comptant 4 minutes par
degré de longitude Est
E est un écart horaire fonction du jour de l’année (en minutes) donné
sur le graphe (III) (ici, pour N = 293, E<0 donc –E>0).
Relever E sur le graphe. E = - 16 min.
Avec DHg1 = 9 mn 24s
et DHg2 = 29 mn,
corrections de longitude pour Paris et Nice respectivement, calculer H1
et H2, heures solaires vraies respectivement à
Paris et
Nice pour ce jour là (N = 293) à cette heure administrative là (Ha =
8h), en appliquant donc la formule (2).
H1 = 6h+9' 24" +16' ~ 6 h 25' .
H2 = 6h+29' +16' = 6 h 45' .
|
|
|