Etude d'un pendule
simple.
Concours Audioprothèsiste Nancy 2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
|
|
|
|
|
|
|
On
étudie l'influence d'un certain nombre de paramètres sur les
oscillations d'un pendule simple. Pour cela, on utilise un système
informatisé d'acquisition des données qui permet d'obtenir l'évolution
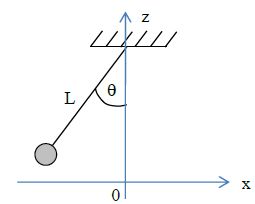
au cours du temps de l'écart angulaire. Dans le plan vertical du
mouvement du pendule, on définit un axe horizontal (Ox) et un axe
vertical (Oz), dont l'origine O coïncide avec la position d'équilibre
du centre d'inertie du mobile.
Intensité de la pesanteur terrestre : g =9,81 m.s-2, intensité de la pesanteur lunaire : g =1,6 m.s-2,
intensité de la pesanteur martienne : g = 3,6 m.s-2.
Influence de l'écart angulaire initial.
On écarte le pendule de sa position d'équilibre de telle sorte que le fil de longueur L fasse un angle q0
avec la verticale, puis on le lâche sans vitesse initiale. On obtient
la courbe suivante après avoir déclenché l'enregistrement au moment du
lâcher.
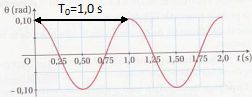 . .
Déterminer la valeur de l'écart angulaire q0 initial en degrés.
0,10 rad soit 0,10 *180 / 3,14 = 5,73 ~5,7°.
Déterminer graphiquement la valeur de la période propre T du pendule. T0 = 1,0 s.
Donner l'expression de la période propre du pendule, puis exprimer la longueur L du pendule en fonction de T0 et g. Calculer la valeur de L.
T0 = 2 p(L / g)½ soit L = T02 g / (4p2).
L = 1,0*9,81 /(4*3,142)=0,2485 m ~0,25 m.
|
| .
. |
|
|
On relève la valeur de la période propre pour différentes valeurs de l'écart angulaire initial q0 :
q0(°)
|
2,0
|
5,0
|
8,0
|
18,0
|
25,0
|
32,0
|
T0(s)
|
1,0
|
1,0
|
1,0
|
1,1
|
1,5
|
1,8
|
Que pouvez-vous remarquer ? Quelle loi est ainsi illustrée ?
Pour des angles inférieurs à 10°, la période ne dépend pas de l'amplitude angulaire. Isochronisme des petites oscillations.
|
.
|
|
Influence de la longueur du pendule.
Pour un même écart angulaire initial, on réalise la même expérience que
précédemment avec des pendules de différentes longueurs L et on
détermine leurs périodes propres T0. On obtient le graphique suivant.
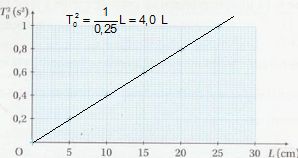
Quelle est la relation mathématique entre le carré de la période propre et la longueur ?
Le carré de la période est proportionnel à la longueur.
Calculer le coefficient directeur K de la droite en s2.m-1. K = 4,0 s2 m-1.
En utilisant l'expression de la période propre, trouver la formule littérale du coefficient directeur K.
Graphiquement T02 = K L. D'autre part T02 =4p2/ g L.
On identifie : K = 4p2/ g.
Déduire des questions précédentes la valeur de l'intensité de la pesanteur et la comparer à celle donnée dans l'énoncé.
g = 4p2/ k = 4*3,142 / 4,0 = 9,87 m s-2.
Ecart relatif : (9,87-9,81) / 9,81 = 0,006 ( 0,6 %).
Influence de l'intensité de la pesanteur.
Sur quel astre (Terre, Lune ou Mars) les oscillations seront-elles les plus lentes ? Justifier la réponse.
La période est inversement proportionnelle à la racine carrée de g. Sur terre la période est la plus faible.
Etude énergétique des oscillations du pendule simple.
Représenter sans souci d'échelle les forces appliquées sur le pendule.
Tension du fil et poids du pendule.
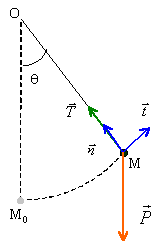
Donner l'expression de l'énergie cinétique du pendule simple. Ec = ½mv2.
Donner l'expression de l'énergie potentielle de pesanteur en fonction de z, puis en fonction de q et L.
Ep = mgz = mgL(1-cos q).
Donner l'expression de l'énergie mécanique totale du pendule.
E = Ec + Ep = ½mv2 +mgL(1-cos q).
Le logiciel d'acquisition des données nous fournit par la suite les évolutions des trois formes d'énergie selon l'abscisse x.
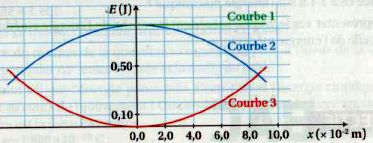
Attribuer à chaque type de courbe, la forme d'énergie correspondante. Justifier votre choix.
Courbe 2 : l'énergie cinétique est maximale pour x = 0.
Courbe 3 : l'énergie potentielle est nulle pour x = 0.
Courbe 1 : énergie mécanique constante en absence de frottement, somme des énergies potentielle et cinétique.
Vérifier la relation entre l'énergie mécanique et les énergies potentielle et cinétique à l'abscisse x=0,060 m.
Ec = 0,62 J ; Ep =0,2 J ; E = 0,82 J. E = Ec +Ep.
Établir les expressions des travaux des forces appliquées au pendule.
La tension, perpendiculaire à chaque instant à la vitesse, ne travaille pas.
Travail du poids entre les altitudes z1 et z2 < z1 : W = mg(z1-z2).
Quelle relation particulière relie la variation d'énergie potentielle au travail d'une des deux forces ?
Le travail du poids est égal à l'opposé de la variation d'énergie potentielle.
|
|
|
Quelle force est responsable du transfert d'énergie au cours du mouvement ?
Le poids est responsable du transfert d'énergie, énergie potentielle / énergie cinétique.
Est-ce qu'une force de frottement agit sur le pendule ?
L'énergie mécanique étant constante, les frottements sont nuls.
|
|
|