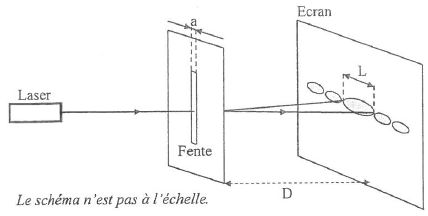
Diffraction, interférences, mesure de l'épaisseur d'une lame de verre. Concours kiné Berck 2015 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . On dispose de 2 lasers: un laser rouge de longueur d'onde l1 et un laser violet de longueur d'onde l2. Diffraction par une fente verticale. La lumière du laser rouge est diffractée par une fente de largeur a. On observe la figure de diffraction sur un écran situé à la distance D de la fente. La tache centrale a une largeur L1. On remplace le laser rouge par le laser violet. Dans les même conditions expérimentales, la tache centrale de diffraction a une largeur L2. l1 = 632 nm ; a = 100 µm ; L1 = 6,83 cm ; L2 = 4,38 cm. Déterminer la valeur de D ( en m). L1 = 2 l1 D /a ; D =L1 a / (2 l1 ) =6,83 10-2 *100 10-6 /(2*632 10-9). D =5,4035 ~5,40 m.   En déduire l2. L2 = 2 l2 D /a. l2= a L2/ (2D) =100 10-6*4,38 10-2 /(2*5,4035). l2=4,053 10-7 m ~ 405 nm. Interférences par des fentes d'Young. 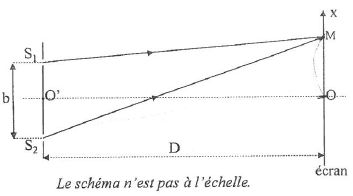On éclaire deux fentes d'Young avec le laser violet. La distance des deux fentes est notée b. O' est le milieu du segment S1S2. La différence de marche d au point M se calcule par : d = S2M-S1M =bx/D. L'interfrange i est la distance qui sépare les milieux de deux franges consécutives de même nature. i =5,85 mm. Calculer b ( en µm). i = l2 D/b ; b = l2 D/ i =4,053 10-7 *5,40 /(5,85 10-3). b = 3,741 10-4 m ~374 µm. Calculer l'interfrange i' ( en mm) si on avait utilisé le laser rouge. i' = l1 D/b  =632 10-9 *5,40 /(3,741 10-4). i' =9,123 10-3 m ~ 9,12 mm. . . Détermination de l'épaisseur d'une lame de verre.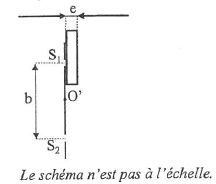 On éclaire à l'aide du laser violet les deux fentes d'Young, mais devant la fente S1, on dispose une petite  lame de verre à faces parallèles, d'indice de réfraction n et d'épaisseur e. On garde les mêmes conditions expérimentales que dans l'expérience précédente. Cette lame augmente le temps du trajet de l'onde lumineuse issue de S1 de t = (n-1) e / c. Les franges d'interférences sont alors décalées vers les x positifs de x0. x0 = 3,62 cm ; n =1,50 ; c = 3,00 108 m/s. Déterminer e en µm. . Soit t = Dt2-Dt1 la différence de durée entre les trajets S2M et S1M. Dt2=S2M/ c ; Dt1=S1M/ c + (n-1)e / c;  t = S2M/ c - (n-1)e / c -S1M/ c = d / c - (n-1)e / c avec d = bx/D. Condition d'interférences constructives : d' =d-(n-1)e = kl2 ; d' / c = d / c - (n-1)e / c  = t = kl2 / c . Or T = l2 / c : t = kT avec T période de l'onde. t = kT = d / c - (n-1)e / c. d = bx/ D ; kT = bx/ (D c) - (n-1)e / c.  x =k D T c / b +(n-1)e D / b.  x =k D l / b +(n-1)e D / b. x =k i+(n-1)e D / b. Pour la frange centrale k = 0 et x0 = (n-1)e D / b. L'ensemble du système de franges est déplacé du côté de la lame. e = bx0 / (D(n-1))=3,741 10-4 *3,62 10-2 /(5,4*0,50)=5,016 10-6 ~5,02 µm. .

menu