Un son peut en
masquer un autre.
Bas S Métropole 09/2016.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
|
|
|
|
|
Les
oreilles captent les sons et le cerveau les interprète. La
psychoacoustique est la science qui étudie l’interprétation des sons
par le cerveau. Un des effets psychoacoustiques, l’effet de masquage,
est étudié dans cet exercice.
1. La fondamentale manquante.
Le cerveau a la capacité de reconstituer certaines informations
manquantes pour construire une perception auditive interprétable. C’est
le cas pour un son musical dont on perçoit la hauteur bien que sa
fréquence fondamentale ait été supprimée. Un son joué par un piano est
numérisé puis transmis. Son spectre après réception est donné
ci-dessous. La composante spectrale correspondant à la fréquence
fondamentale a été supprimée au cours d’un traitement spécifique du
signal.
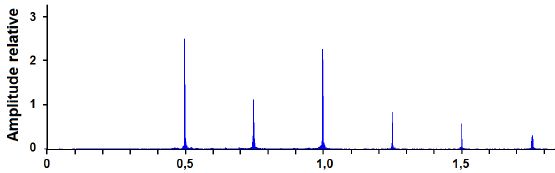
Déterminer la hauteur du son joué par le piano. Expliquer votre raisonnement.
Les fréquences des harmoniques sont un multiple de la fréquence du fondamental ( hauteur du son).
Les fréquences des harmoniques sont un multiple de 0,25 kHz
La fréquence du fondamental, la hauteur du son, est 0,25 kHz.
2. L’effet de masquage
Si deux sons purs sont écoutés simultanément, le plus intense, appelé
son masquant, peut créer une gêne sur la perception du second, le son
masqué. Il peut même le rendre inaudible. La comparaison des courbes
des figures 1 et 2 données à la suite, permet de mettre en évidence ce
phénomène psychoacoustique appelé « effet de masquage ».
Le graphique
suivant indique les valeurs minimales de niveau d'intensité sonore
audible en fonction de la fréquence lorsque le son est écouté en
environnement silencieux.
Figure 1 : seuil d'audibilité humaine en fonction de la fréquence.
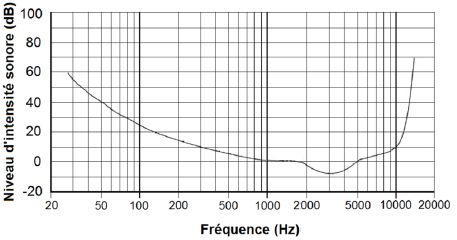
Exemple de lecture : un son de fréquence 80 Hz doit avoir un niveau sonore supérieur à 30 dB pour être audible.
|
|
|
Figure 2 : seuil d’audibilité humaine d’un son en présence d’un son masquant de niveau d’intensité
sonore 55 dB et de fréquence 1 kHz.
Le graphique suivant indique les valeurs minimales de niveau
d'intensité sonore audible en fonction de la fréquence lorsque le son
est écouté simultanément avec un son pur de fréquence 1kHz et de niveau
d’intensité sonore 55 dB.
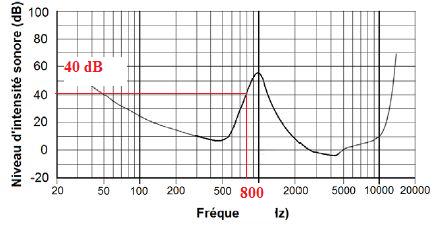
2.1.
Déterminer le niveau d’intensité sonore minimal pour qu’un son de
fréquence 800 Hz soit audible en présence d’un son masquant de
fréquence 1 kHz et de niveau sonore 55 dB.
Un son de fréquence 800 Hz doit avoir un niveau sonore supérieur à 40 dB pour être audible en présence du son masquant cité.
|
|
|
|
Le format MP3 exploite l’effet de masquage pour compresser l’enregistrement numérique d’un signal sonore.
Cela consiste à réduire l’information à stocker sans trop dégrader la
qualité sonore du signal. La compression de l’enregistrement permet
donc de réduire le « poids » numérique (ou la taille du fichier) d’un
enregistrement musical.
Le spectre fréquentiel de la note La3 jouée par une flûte traversière dans un environnement silencieux est donné ci-dessous.
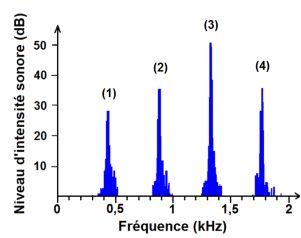
La
flûte joue la note La3 en présence d’un son masquant de fréquence 1 kHz
et de niveau d’intensité sonore de 55 dB qui correspond au cas de la
figure 2. L’enregistrement numérique du signal sonore est compressé au
format MP3.
2.2. En étudiant chaque pic du spectre de la figure, indiquer celui ou ceux qui seront éliminés par ce codage MP3. Justifier.
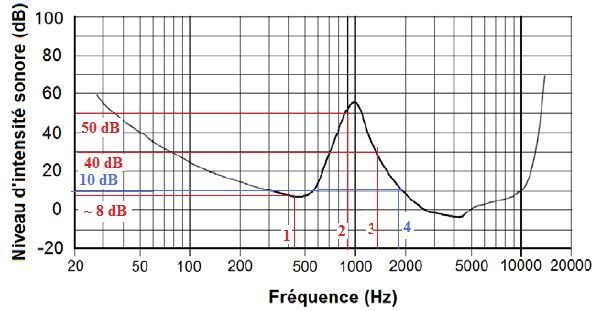
Le pic n°2 est éliminé : pour être audible le niveau d'intensité sonore doit être supérieur à 50 dB.
2.3. Une chanson de
3 minutes est enregistrée sur un CD. Cet enregistrement est compressé
au format MP3. Le « poids » numérique du fichier obtenu est alors égal
à 2,88 106 octets. À l’aide des données, déterminer le facteur de compression du format MP3 après en avoir proposé une définition.
Débit binaire lors de la lecture d’une musique enregistrée sur CD : 1,41×106 bits.s-1.
Débit binaire du fichier compressé : 2,88 106 *8/(3*60)=1,28 105 bits.s-1.
Facteur de compression = débit binaire los de la lecture / débit binaire du fichier compressé =14,1 / 1,28 =11,0.
|
|
.
2.4. Effet de masquage lors du passage d’un train
Dans une ambiance sonore calme deux personnes conversent à un mètre
l’une de l’autre. L’auditeur perçoit la parole de l’orateur avec un
niveau d’intensité sonore égal à 50 dB.
Un train passe. La parole de l’orateur est masquée par le bruit du
train. On suppose que dans ces conditions, le bruit du train masque
toutes les fréquences audibles.
On admettra que le niveau d’intensité sonore minimal audible de la
parole, en présence du train, est égal à 60 dB quelle que soit la
fréquence. Pour être entendu, l’orateur parlera plus fort ou se
rapprochera de son auditeur.
2.4.1. L’orateur ne
se rapproche pas mais parle plus fort. Là où se trouve l’auditeur, le
niveau d’intensité sonore est de 70 dB, déterminer s’il perçoit le son.
Il perçoit le son : le niveau d'intensité sonore perçu est de 70 dB,
valeur supérieure au niveau d'intensité sonore minimal audible en
présence du train ( 60 dB).
Pour une source isotrope (c'est-à-dire émettant de la même façon dans
toutes les directions), l’intensité sonore en un point situé à une
distance d de la source est inversement proportionnelle à d2, c'est-à-dire que l’intensité sonore I =k /d2 où k est une constante.
2.4.2. Si l’orateur
ne parle pas plus fort mais se rapproche de l’auditeur, à quelle
distance de l’auditeur devra-t-il se placer pour être audible ?
Justifier.
A un niveau sonore de 50 dB : I = I0 10L/10 =10-12 * 105 = 10-7 W m-2 ; I = k / d2 avec d = 1 m ; I = k.
A un niveau sonore de 60 dB :
I mini = 10-12 * 106 = 10-6 W m-2 ; Imini = k / d2min = I / d2min ;
d =[I / Imini ]½ =0,10½ =0,32 m.
|
|