L'effet Doppler peut-il perturber un danseur ? Bac S Amérique du Sud 2016. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . Lors de la répétition générale d’un ballet, Alice, la pianiste, ponctue la fin du 1er acte en jouant une série de La3 successifs au cours desquels Kilian, le danseur, effectue un saut appelé « grand jeté ». Après le baisser du rideau, le directeur artistique trouve Kilian et Alice en pleine discussion. Kilian a perçu des La3 successifs qui lui semblaient de hauteurs différentes et pense qu’Alice n’a pas joué la même note. Alice conteste et affirme qu’elle a bien joué la même note. L’objectif de l’exercice est de comprendre l’origine de ce désaccord. Tableau du déroulement chronologique de la fin du premier acte. 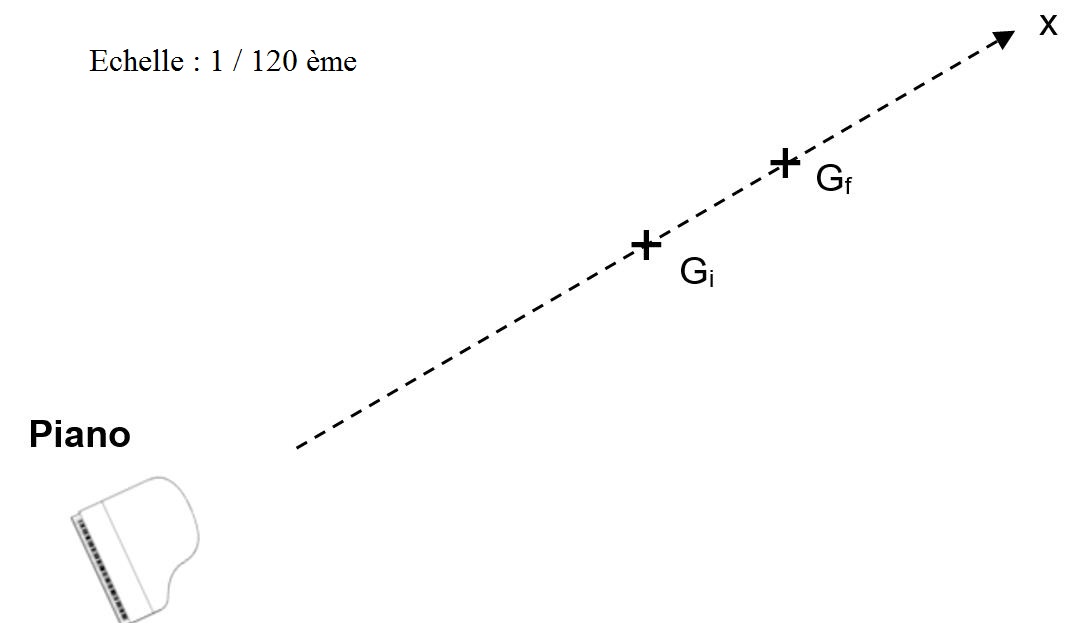Pianiste Mi3 Si3 Ré3 La3 La3 La3 La3 La3 La3 La3 Danseur immobile course d'élan et grand jeté Données On adoptera les notations suivantes : G représente le centre de gravité de Kilian,  Gi est la position de G au début du grand jeté ; Gf est la position de G à la fin du grand jeté,  Dt est la durée du grand jeté (Dt = 0,710 s). . 1. Détermination de la vitesse de Kilian 1.1. Déterminer la distance horizontale parcourue par Kilian lors de son grand jeté. 1.2. En déduire la vitesse horizontale moyenne de Kilian lors de son grand jeté. G1G2  = 1,8 x120 / 100 =2,16 m. v = G1G2 / Dt = 2,16 / 0,710 = 3,04~3,0 m /s. On supposera dans la suite de l’exercice que la vitesse horizontale du danseur reste constante lors du grand jeté. 2. Fréquence du son perçu par Kilian 2.1. Quelle est la fréquence des notes émises par le piano pendant le grand jeté de Kilian ? Mi3 : 330 Hz ; Si3 : 494 Hz ; Ré3 : 294 Hz ; La3 ; 440 Hz. 2.2. Quelle est la fréquence des notes perçues par Kilian pendant son grand jeté ? Expliquer en détail votre raisonnement et votre calcul (on ne prendra en compte que la composante horizontale du mouvement de G). Si le récepteur s’éloigne de l’émetteur, la fréquence perçue est : fR = fE(vson /(vson +v). fR =440(340 /(340 +3,0) = 436 Hz. 2.3. Sachant que Kilian a une oreille entraînée par des années d’études musicales, expliquer s’il peut percevoir cette différence de hauteur. L’oreille humaine n’est capable de percevoir la différence de hauteur entre deux sons successifs que si la variation relative des fréquences entre ces deux sons, notée Df / f est supérieure ou égale à une certaine valeur appelée seuil différentiel relatif, Sdr. Pour une oreille entraînée, Sdr = 1 /1000, quelle que soit la fréquence. (440-436) / 440 ~9 10-3, valeur supérieure à 10-3. Kilian perçoit cette différence de hauteur du son. 2.4. Un autre danseur n’ayant pas l’oreille entraînée, aurait-il été capable de percevoir cette différence de fréquence ? Pour une oreille non entraînée, Sdr ~ 3 10-3 à 440 Hz. (440-436) / 440 ~9 10-3, valeur supérieure à 310-3. Une oreille non entraînée perçoit cette différence de hauteur du son. 3. Discussion entre Alice et Kilian. Expliquer l’origine du désaccord entre Alice et Kilian. Alice, la pianiste, est immobile par rapport à l'émetteur, le piano. L'émetteur et le récepteur ne sont pas en mouvement relatif : l'effet Doppler ne se manifeste pas. Kilian n'est pas immobile par rapport à l'émetteur, le piano. L'émetteur et le récepteur sont pas en mouvement relatif, Kilian s'éloigne du piano : l'effet Doppler se manifeste. Le son perçu par Kilian en mouvement est plus grave et son oreille entraînée le perçoit. .

menu