Satellisation. Concours ingénieur ITPE 2016.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.



. .



.
.



La terre est assimilable à une sphère de rayon R = 6400 km. Elle effectue un mouvement de rotation uniforme de période T = 24 h dans le référentiel géocentrique supposé galilléen. On donne l'intensité de la pesanteur à la surface de la terre g0 = 9,8 m s-2. On admettra que l'énergie mécanique d'un satellite en orbite elliptique est identique à celle d'un satellite en orbite circulaire moyennant la substitution r <-->a où r et a représentent respectivement le rayon et le demi-grand axe de l'ellipse.

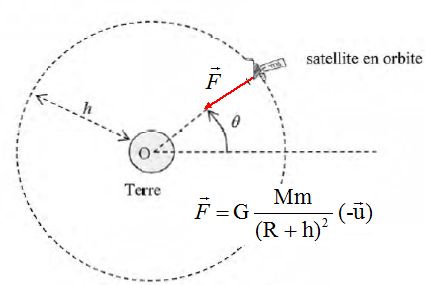Orbite circulaire à faible altitude.
L'altitude du satellite est très inférieure à celle du rayon terrestre.
1.1. Rappeler l'expression de la vitesse et de l'accélération d'un point mobile en coordonnées polaires.
1.2. Démontrer que la composante radiale de l'accélération est égale à v2 / R.



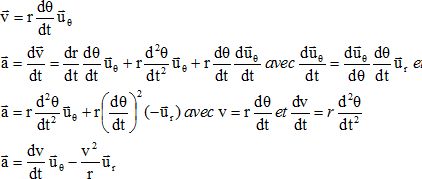
 1.3 On pourra utiliser le principe fondamental de la dynamique au satellite pour exprimer la vitesse v et en déduire la période T0 du satellite.

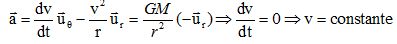
La valeur de la vitesse étant constante, le mouvement est uniforme.
 v2 = GM/r = GM((R+h) ; v = (GM/(R+h))½.
 Le satellite décrit la circonférence 2p(R+h) à la vitesse v en T0 secondes.
v = 2p(R+h) / T0 ; v2 = 4 p2(R+h)2/T02.
or v2 = GM / (R+h) : 4 p2(R+h)3/T02 = GM ou T02 = 4 p2(R+h)3/(GM). ( 3è loi de Kepler).
Dans toute la suite, on pourra admettre que v2 = g0 R.
1.4. Calculer la vitesse vs d'un point situé à l'équateur au niveau de la surface terrestre. Exprimer le rapport vs / v en fonction de g0, R et T1. Discuter.
vs=(GM / R)½ avec GM = g0R2.
vs=(g0R)½= (9,8 x 6,4 106)½ ~7,9 103 m/s.
vs = 2pR / T1 ; vs / v =2pR½ / (T1 g0½).




1.5. Exprimer l'énergie W0 à communiquer au satellite pour qu'il puisse atteindre cette orbite depuis une base de lancement située sur terre en fonction de son énergie cinétique Ec sur son orbite.
En orbite à l'altitude h : énergie cinétique : Ec = ½mv2  avec v2 = GM/(R+h) ;  Ec = ½mGM/(R+h) ;
Em = Ep+Ec =  -GMm /(R+h) + ½mGM/(R+h)  = -½mGM/(R+h)= -Ec.
½mGM = Ec(R+h)
Au niveau du sol terrestre : Em sol = Ep sol+Ec sol =  -GMm /R + ½mGM/R  = -½mGM / R.
W0 = Em - Em sol = -½mGM/(R+h) + ½mGM / R = ½mGM[ 1 / R -1/(R+h)]=Ec[(R+h)/R-1]

 Mise en orbite.
En un point de l'orbite basse on communique très rapidement une nouvelle vitesse v' afin que le satellite puisse, par l'intermédiaire d'une trajectoire elliptique, arriver tangentiellement à l'orbite géostationnaire.

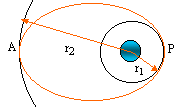
 2.1. Exprimer v' en fonction de v et du rapport d = r2 /R où r2 représente le rayon de l'orbite géostationnaire.
2.2. Exprimer le travail W1 lié à cette étape en fonction de Ec et d.
L'énergie mécanique sur la trajectoire elliptique se conserve.
Aux points A et P : Em = - GMm / (r1 +r2).= -½mv ' 2.
Energie mécanique sur l'orbite circulaire basse :
au point P : Em1 = -½ mGM / r1 = -Ec = -½mv2.
(v' / v)2 =2 r1 / (r1+r2) ; or r1 ~R : v' / v ~(2 / (1+d))½.
Variation d'énergie mécanique en P : DE = Em -Em1 = - GMm / (r1 +r2) + ½ mGM / r1
DE =GMm (r2 - r1) / [2(r1 +r2)r1].
DE =2Ecr1 (r2 - r1) / [2(r1 +r2)r1]
DE =Ec (r2 - r1) / (r1 +r2).
DE =Ec (d - 1) / (d+1) = W1.
Cette valeur est positive, la vitesse du satellite augmente.









2.3 Quelle est en fonction de v' et de d la vitesse v1 du satellite lorsqu'il arrive tangentiellement à l'orbite géostationnaire ?
2.4. Au point où le satellite arrive tangentiellement à l'orbite géostationnaire, on lui communique  la vitesse v1. Exprimer le travail W2 dépensé dans cette opération en fonction de Ec et de d.
Energie mécanique sur l'orbite circulaire haute :
au point A : Em2 = -½ mGM / r2 = -Ec = -½mv12.
(v1 / v')2 =(r1+r2) / (2r2) ; or r1 ~R : v1 / v' ~((1+1/d) /2)½.
Variation d'énergie mécanique en A : DE' = Em2 -Em = - ½ mGM / r2+ GMm / (r1 +r2) 
DE' =GMm (r2 - r1) / [2(r1 +r2)r2].
DE' =2Ecr1 (r2 - r1) / [2(r1 +r2)r2]
DE' =Ec (r2 - r1) / [(r1 +r2)d].
DE' =Ec (d - 1) / [(d+1)d]= W2.

2.5 En déduire le travail total W' nécessaire à la mise en orbite géostationnaire du satellite.
W' = W0 +W1 +W2.


.
.


  

menu