Physique, concours officier chef de quart marine 2016.

Physique, concours officier chef de quart marine 2016.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

.
.

Exercice 1.
Une remorque de poids P appliqué en G, est à l'arrêt sur un plan horizontal telle que représentée sur la figure ci-dessous.
1. Soient F_A et F_B les forces appliquées respectivement en A point de contact de la roue avec le sol, et B point de contact entre la rotule de l'attelage et la remorque.
Déterminer les directions de F_A et F_B.
A l'équilibre la somme des trois vecteurs forces est nulle ; les forces ont la même direction verticale.

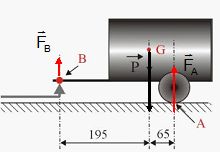
2. Pour P = 2000 daN, déterminer l'intensité de F_A.
Moment des forces en G :
-1,95F_B +0,65 F_A = 0 soit F_B =0,65 F_A /1,95 ~0,333 F_A.
P = F_A +F_B = 2000 ; (1+0,333) F_A = 2000 ; F_A = 2000 / 1,333 =1500 daN.
3. En déduire l'intensité de F_B.
F_B = 200-1500 = 500 daN.
4. Vérifier les résultats obtenus en calculant le moment résultant en A.
Moment en A de F_A = 0, la direction de la force rencontre l'axe de rotation.
Moment en A du poids : -0,65 P .
Moment en A de F_B : + 1,95 F_B.
A l'équilibre la somme des moments est nulle :
-0,65 P +(1,95+0,65) F_B = 0 ; F_B =0,65*2000 / 2,6 =500 daN.
F_A = 2000-500 ~ 1500 daN.

Exercice 2.
Une voiture arrive au sommet d'une côte à la vitesse de 54 km.h^-1, à ce moment, elle passe au point mort et descend en roue libre une cote de 10 % sur une longueur de 800 m. Il n'y a pas d'action sur les freins, la résistance de l'air et les frottements sont négligés.
1. Déterminer le temps de la descente.
Vitesse initiale : v_i=54 / 3,6 = 15 m/s.
tan a ~sin a = 0,10.
Accélération du véhicule : a = g sin a = 10*0,1 = 1 m s^-2.
Vitesse à la date t : v = g sin a t +v_i.
Position à la date t : x = ½ g sin a t² +v_it = 5*0,10 t² +15t.
En bas de la cote : 800 = 0,5 t² +15 t.
Il faut résoudre : 0,5 t² +15 t -800 = 0.
Discriminant : D = 15²+4*0,5*800 =1825 ; D^½ = 42,7
Solution positive :( -15 * 42,7) / (2*0,5)=27,7 s.
2. Déterminer la vitesse du véhicule au bas de la côte.
L'origine des altitudes est le bas de la cote.
La route s'élève de 1 m tous les 10 m ; altitude initiale : 800 *0,1 = 80 m.
L'énergie mécanique initiale est sous forme potentielle et cinétique: mgh+½mv_i²..
L'énergie mécanique finale est sous forme cinétique : ½mv_f².
L'énergie mécanique se conserve : ½mv_f²=mgh+½mv_i².
.v_f²=2gh+v_i² = 2*10*80 +15² =1825.
v_f = 42,7 m /s.

Exercice 3.
Soient deux axes perpendiculaires Ox et Oy. Un point P se déplace dans le plan xOy. Les mouvements des projections p et p’ sur les axes Ox et Oy sont définis, en unités S.I., par les relations suivantes :
Op = x = 2 cos t + 3 ;
Op' = y = 2 sin t + 1.
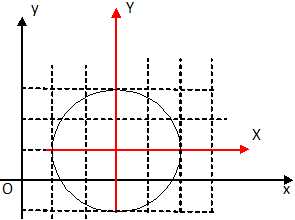
1. Montrer que le mouvement de P est circulaire et uniforme.
On effectue un changement devariables : X = x-3 et Y = y-1.
X² +Y² = (2 cos t )² +(2 sin t)² =4 cos² t +4 sin² t .
X² +Y² =4. La trajectoire est un cercle de rayon R = 2.

2. Montrer que la vitesse est constante.
X' = -2 sin t ; Y' = 2 cos t ; X'² +Y'² = 4 sin²t +4 cos²t = 4 ; v = 2 m s^-1.
La norme de la vitesse étant constante, le mouvement est uniforme.
3. Calculer w la vitesse angulaire.
w = v / R = 2 / 2 = 1 rad s^-1.

Exercice 4.
Le circuit ABCD ci-contre est constitué de la manière suivante :
U_AB est une source de tension continue telle que U_AB = 1000 V;
R_fune résistance telle que R_f= 700 ohms ;
R_h un rhéostat réglable entre 0 et 200 ohms.

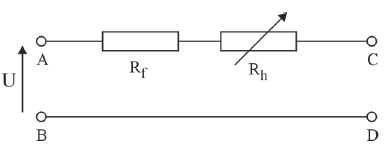
1. On désire brancher entre les bornes C et D deux lampes L₁ et L₂, en parallèle, dont les caractéristiques sont les suivantes :
L₁ : 220 V – 200 W ; L₂ : 220 V – 25 W.
a. Calculer la valeur de R_h pour qu'elles fonctionnent normalement.
U_CD = 220 V ; U_AC = U-U_CD =1000-220 =780 V.
Intensité dans L₁ : 200 / 220 ~0,91 A. Intensité dans L₂ : 25 / 220 ~0,114 A.
Intensité dans la branche AC : I = 0,91 +0,114 = 1,023 A
U_AC =(R_f +R_h) I ; R_h= U_AC / I-R_f =780 /1,023 -700 ~62,7 ohms.
b. Déterminer la tension aux bornes de la lampe L₂ si la lampe L₁ vient à griller.
La lampe grillée se comporte comme un interrupteur ouvert.
Résistance de L₂ : R₂ = 220² / 25 =1936 ohms.
Résistance totale de la branche ACD : 1936+700+62,7 ~2698,7 ohms.
Intensité du courant : 1000 / 2698,7 = 0,37 A
L₂ est traversée par un courant trop intense, elle va rapidement griller et la tension à ces bornes sera égale à U.
Tension aux bornes de L₂ avant qu'elle ne grille : 1936 *0,37 ~716 V.
2. On désire désormais alimenter deux lampes de 110 V – 100 W en série entre les bornes C et D :
a. Montrer qu'elles peuvent fonctionner normalement.
En fonctionnement normal, la tension aux bornes des deux lampes en série est 110 +110 = 220 V.
Résistance de chaque lampe : R = 110² /100 = 121 ohms.
Intensité du courant dans chaque lampe : I = 100 / 110 =0,91 A.
Intensité dans la branche AC : 0,91 A.
b. Déterminer la nouvelle valeur de R_h correspondante.
U_AC = U-U_CD =1000-220 =780 V.
U_AC =(R_f +R_h) I ; R_h= U_AC / I-R_f =780 /0,91 -700 ~158 ohms.
c. Déterminer la tension aux bornes de la lampe L₂ si la lampe L₁ vient à griller.
Les lampes étant en série, si l'une grille, l'autre ne fonctionne plus ; la tension aux bornes de L₂ est nulle ; la tension aux bornes de L₁ est égale à U.

menu