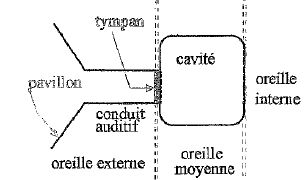
Modèlisation de l'oreille externe et moyenne. Concours interne ingénieurs de l'Industries et des Mines 2016. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . L'oreille se décompose en trois parties. Oreille externe : le pavillon ouvert à l'air libre collecte les sons vers le conduit auditif. Oreille moyenne : elle amplifie les signaux mécaniques de l'oreille externe vers l'oreille interne. Oreille interne : elle transforme les signaux mécaniques en signaux électriques vers le nerf auditif. A. Oreille externe. Le tympan est assimilé à une membrane de masse m = 0,015 g vibrant parallèlement à elle-même selon l'axe Ox. Le déplacement par rapport à l'équilibre est noté x(t). 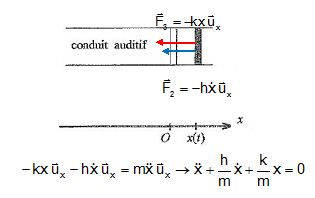La pesanteur n'intervient pas mais le tympan est soumis à : une force de rappel F3 = kx avec k = 3500 N m-1 ; une force de frottement F2 = h x' avec h = 0,1 N s m-1. A.1. Ecrire puis résoudre l'équation différentielle décrivant l'évolution du tympan. A.2 Vérifier que le régime est oscillatoire et calculer t et w. On pose w02 = k / m  = 3500 /1,5 10-5 =2,33 108 ( rad/s)2 ; w0 = 1,5 104 rad/s.   et t = m /(2h) =1,5 10-5 /(0,2) = 7,5 10-5 s. x" + 2 / t x' +w02 x=0. D = 4 / t2-4w02 = 4[1 / t2-w02 ] = -4w2 = -2,2 108 ; w = 7,4 103 rad/s.  D est négatif, le régime est oscilatoire amorti.  Solutions x = -1/ t ±jw. Solutions de l'équation différentielle : x = X0 exp(-t / t) exp (jwt) avec X0 une constante. A.3. A ce modèle mécanique, correspond formellement un modèle électrique fait d'un circuit série avec une résistance R, Une inductance L et une capacité C. La variable x(t) étant remplacée par la variable q(t) charge de la capacité. Sachant que R = 100 ohms et L = 15 mH calculer C. A.4. Vérifier que la durée typique d'amortissement est bien la même pour le modèle électrique. A la masse m correspond l'inductance L ; à la résistance correspond le coefficient de frottement h ; à l'inverse de la capacité correspond la raideur. w02 = 1 / ( LC)  =2,33 108 ( rad/s)2 ;  C =1 / (Lw02) =1 /(0,015* 2,33 108 )=2,9 10-7 F.   et t = L /(2R) =1,5 10-2 / (200) = 7,5 10-5 s. A.5. Un son se traduit physiquement par une modification de pression. Ainsi le tympan est soumis en plus à une force de pression. Comment faut-il modifier alors le circuit électrique dual ? Il faut ajouter une source de tension idéale de force électromotrice e(t). Pour tenir compte de la présence du conduit auditif avant le tympan, au modèle électrique précédent, il faut ajouter une inductance L' et une capacité C' en série. On définit la fonction de transfert par H(jw) = s(t) / e(t) avec e(t) = E0 exp(jwt) avec j2 = -1. 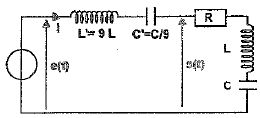A.6. Montrer qu'il s'agit pour H(jw) d'une fonction de transfert d'un filtre passe-bande. 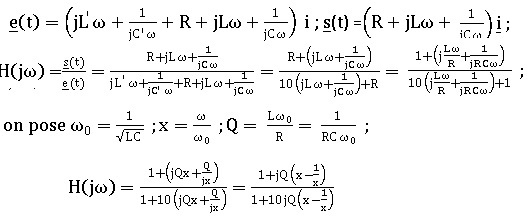. A.7. Pourquoi est-on amené à devoir forcément modéliser par un filtre passe-bande ? Et en quoi le circuit proposé n'est-il pas pertinent ? L'oreille humaine perçoit les sons dont les fréquences sont comprises entre 20 Hz et 20 000 Hz. Le circuit n'est pas pertinent car la sensibilité de l'oreille dépend de la fréquence. La sensibilité est maximale pour une fréquence de  1000 Hz. L'oreille moyenne. Elle se modèlise par une cavité remplie d'air, initialement à la température T0 et à la pression standard P0. Cette cavité comporte deux membranes mobiles, la première ( le tympan) de section S et d'abscisse x(t) par rapport à sa position au repos, et  l'autre de même section S et d'abscisse  x'(t) par rapport à sa position au repos, comme indiqué ci-dessous. 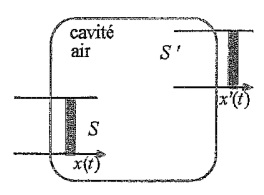Le volume de la cavité est V0 au repos. Lorrsque ces membranes sont en mouvement, le volume V et la pression P de la cavité seront supposés s'écarter très faiblement de leurs valeurs d'équilibre. L'air  est assimilé à un gaz parfait pour lequel le rapport des capacités thermiques est noté g. B.1. Exprimer dV = V-V0 en fonction de S, dx et dx'. V  = V0-Sdx+Sdx'  ; dV = S( dx'-dx). B.2. L'air de la cavité évolue de manière adiabatique. Avec l'équation de Laplace, relier la variation de pression dP dans la cavité à la variation de volume dV, ainsi qu'à la pression P0, le volume V0 et à g. PVg = P0V0g ;  dP / P + gdV / V=0 ; dP / P + gdV P /P0]1/g /V0.  dP / P = -g / V S(dx'-dx). B.3. Déduire l'expression de la variaation de pression P-P0 en fonction de g, S, x, x', P0 et V0. 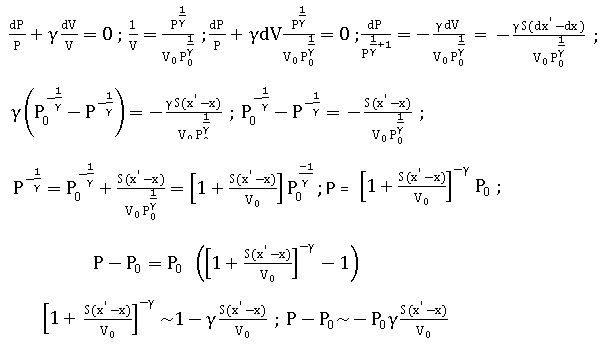B.4. Exprimer les forces de pression sur chacune  des membranes. F = (P-P0)S= SdP. Un modèle simple pour étudier le mouvement des deux membranes est le suivant. Les deux membranes possèdent des masses m et m' =  4 m et sont soumises à des forces de rappel de constante de raideur k = mw02 et k' = 4mw02. Il n'y a pas de frottement, mais on prend en compte fes forces de pression engendrées sur chacune des deux membranes par l'écart de pression dP dans la cavité et la force sonore externe F(t) sur la première membrane B.5. Ecrire les  deux équations différentielles régissant les positions x  et x' des membranes. m d2x / dt2 = F(t)-k x-SdP (1). 4m d2x' / dt2 = -4k x'-SdP (2). B.6. Dans le cas où F(t) =F0 exp(jwt), les déplacements des membranes sont sinusoïdaux de même pulsation x(t) = X0 exp(jwt) et x'(t) = HX0 exp(jwt). Exprimer le rapport H en fonction de w, w0 et W = [gP0S2 / (4mV0)]½. (2) s'écrit : - 4mw2HX0 exp(jwt)= -4k HX0 exp(jwt)+S2P0g /V0(H-1)X0 exp(jwt). - 4mw2H= -4k H+S2P0g /V0(H-1). - 4mw2H+4k H-S2P0g /V0 H= -S2P0g /V0 H(4mw2-4mw02+S2P0g /V0)=S2P0g /V0. H(w2-w02+S2P0g /(4mV0))=S2P0g /(4mV0). H(w2-w02+W2)=W2. H =W2/(w2-w02+W2). B.7. Tracer la courbe H(w). .

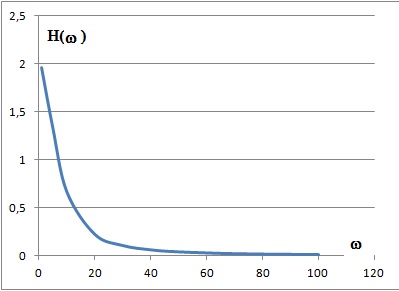
menu