Le laser Erbium-YAG. Concours orthoptie Nantes 2016. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Dans ce laser le milieu amplificateur est solide. C'est un cristal de YAG ( grenat d'yttrium et d'aluminium ) dopé en ion Erbium Er3+, dont les niveaux d'énergie sont représentés ci-dessous. Ils sont le siège d'absorption et d'émission simulée. La longueur d'onde la mieux adaptée à l'absorption du barreau d'Erbium-YAG est de 980 nm. La longueur d'onde du rayon laser vaut 2936 nm. Partie A. 1. Sur le diagramme énergétique représenter la transition correspondant à une absorption maximale.   2. Décrire le phénomène d'émission stimulée entre le niveau E2 et E1. Quels sont les caractéristiques du photon émis ? On peut aussi favoriser la désexcitation d’un électron en envoyant sur l’atome excité une lumière ( onde électromagnétique) dont la longueur d’onde correspondant à l’énergie de transition entre les deux états électroniques. On appelle ce phénomène l’émission stimulée (ou émission induite). Il y a amplification si les atomes sont plus nombreux à être dans l'état n' ( atome excité susceptible d'émettre) que dans l'état n (susceptible d'absorber) : il est nécessaire d'avoir une « inversion de population ». L’émission stimulée d’un atome ou d’une molécule donne un nouveau photon qui a exactement les mêmes fréquence, phase et direction que le photon incident ; dans un laser, cela se fait sur un très grand nombre d’atomes ou molécules identiques. Un laser émet une onde lumineuse intense dont la direction, la fréquence et la phase sont très bien déterminées. ( lumière cohérente). 3. Calculer l'écart d'énergie entre le niveau E1 et E3. E3-E1 = h c / l = 6,63 10-34 *3,00 108 / (980 10-9) =2,03 10-19 J. 4. Dans quel dommaine du spectre électromagnétique émet ce laser ? 2936 nm appartient au domaine infrarouge. . . 5. Calculer l'écart d'énergie entre le niveau E1 et E2.  E2-E1 = h c / l = 6,63 10-34 *3,00 108 / (2936 10-9) =6,77 10-20 J.. 6. Comparer l'énergie reçue et l'énergie émise par cet atome et expliquer pourquoi ce laser nécessite un système de refroidissement. L'énergie reçue est supérieure à l'énergie émise. Il faut évacuer la chaleur produite dans le cristal, énergie libérée dans le cristal lors de la désexcitation non radiative E3--> E2. 7. Donner deux caractéristiques générales d'un faisceau laser. Le faisceau est très directif ; la puissance par unité de surface est très grande. Partie B. Ce laser émet des impulsions avec une cadence de tir de fréquence f = 10 Hz ( 10 impulsions par seconde ). Chaque impulsion a une durée t = 0,20 ms et une énergie DEimp = 300 mJ. 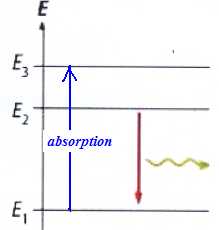1. Calculer le nombre de photons émis par impulsion, sachant que chaque photon a une énergie Ephoton = 6,76 10-20 J. Energie fournie par impulsion : 300 mJ = 0,3 J. Nombre de photons émis : 0,3 / 6,76 10-20 =4,44 1018 photons. 2. Calculer la puissance lumineuse d'émission d'une impulsion. Puissance ( W) = énergie (J) / durée (s) = 0,3 / (0,20 10-3) = 1,5 103 W. Le spot de ce laser a un rayon r = 0,5 mm. 3. Calculer l'intensité ( ou puissance surfacique) du Laser. Aire du spot circulaire : pi r2 = 3,14 * (0,5 10-3)2 = 7,854 10-7 m2. Puissance moyenne du laser : = énergie de 10 impulsions par seconde = 10*0,3 = 3,0 W. Puissance surfacique = puissance moyenne (W) / surface (m2) = 3,0 / 7,854 10-7 =3,8 106 W m-2. 4. L'énergie rayonnante émise au cours d'une séance de durée Dt a pour expression : DEray = f Dt DEimp. a. Montrer que DEray a la dimension d'une énergie. DEimp. ala dimension d'une énergie ; f est l'inverse d'un temps et Dt est une durée.  f Dt est sans dimension. DEray a la même dimension que  DEimp, celle d'une énergie. b. Déterminer cette énergie pour une durée Dt = 4,5 s. 45 impulsions en 4,5 s ; énergie rayonnante d'une impulsion : 0,3 J. Energie lumineuse des 45 impulsions : 45*0,300 =13,5 ~14 J. .

menu