La lumière, une onde, scintigraphie,électrostatique et magnétostatique. Concours EMIA 2011. école militaire interarmes

La lumière, une onde, scintigraphie, électrostatique et magnétostatique. Concours EMIA 2011.
école militaire interarmes

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

.
.

Exercice 1 : Chute ( 2 / 7).
1.1. Donner la définition d'une onde mécanique.
Une onde mécanique est la propagation d'une perturbation dans un milieu matériel avec transport d'énergie, sans transport de matière.
1.2. Définir ce qu'est une onde mécanique longitudinale et donner un exemple. Même question pour une onde mécanique transversale.
Longitudinale : la direction de déformation du milieu est identique à la direction de propagation. Exemple : les onde sonores.
Transversale : la direction de déformation du milieu est perpendiculaire à la direction de propagation. Exemple : la houle.
1.3. Quelle erreur Huygens commet-il en comparant la propagation de la lumière à celle des ondes mécaniques ?
La lumière peut se propager dans le vide, contrairement aux ondes mécaniques. Une onde ne transporte pas de matière,mais de l'énergie.
1.4. Le phénomène de diffraction étudié par Fresnel est-il compatible avec le principe de propagation rectiligne de la lumière ? Préciser.
Oui : dans un milieu homogène, la lumière se propage en ligne droite, excepté lorsqu'elle rencontre un obstacle ou une fente dont les dimensions sont du même ordre de grandeur que la longueur d'onde de l'onde.
1.5. Ce phénomène de diffraction est-il un argument en faveur de la nature ondulatoire de la lumière ? Préciser.
Oui : la diffraction est un phénomène caractéristique de toutes les ondes.
1.6. Le diamètre du fil de fer a t-il une influence sur la figure de diffraction qu'il observe ? Préciser.
Oui : la diffraction est d'autant plus marquée que le diamètre du fil de fer et plus proche de la longueur d'onde de la lumière.
A propos de la diffraction.

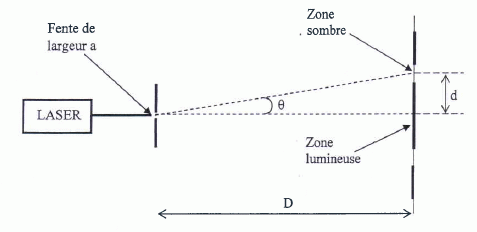
1.7. Donner la relation entre L = 2d, q et D qui permet de calculer q pour chaque fil.
tan q = ½L / D ~ q radian pour les petits angles.
q = l / a avec a, diamètre du fil.
Par suite : a = 2lD / L.
1.8. A partir des mesures effectuées, on représente les variations de q en fonction de 1/a. Ces données expérimentales sont-elles en accord avec la relation théorique q = l/a ? Justifier.

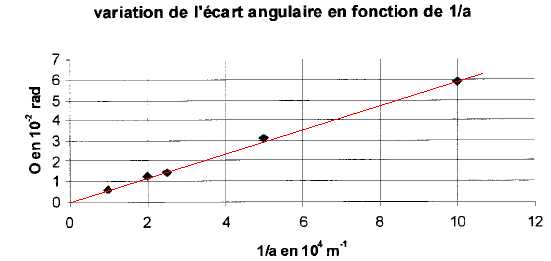
Oui, le graphe est une droite passant par l'origine. La pente de la droite est égale à l.
1.9. En déduire une valeur approchée de l.
Pente : 6 10^-2 / (10 10⁴) = 6 10^-7 m ~0,6 µm.

La scintigraphie ( 2 / 20).
L'iode 123 permet le suivi des cancers thyroïdiens. Il est radioactif et se désintègre par capture électronique en émettant un rayonnement g. Son temps de demi-vie t_½ = 13,2 h.
Deux à trois heures avant l'examen on injecte par voie intraveineuse, une dose d'iode 123 qui présente une activité A₀ = 70, MBq.
2.1. Rappeler la composition du noyau d'iode 123 ¹²³₅₃I.
53 protons et 123-53 = 70 neutrons.
2.2. Comparer la masse totale que possèdent les nucléons qui participent àla formation de ce noyau à la masse du noyau d'iode 123 ( 122,876523 u).
53 m_P +70 m_N = 53*1,007825 +70*1,008665 =53,414725 + 40,60655 =124,021275 u.
La masse du noyau est inférieure à la somme des masse de ces constituants au repos.
2.3. L'iode 123 est obtenu en bombardant du tellure ¹²²₅₂Te par des noyaux de deutérium²₁H.
Ecrire l'équation de cette réaction nucléaire en identifiant la particule libérée.
¹²²₅₂Te + ²₁H -->¹²³₅₃I + ¹₀n ( neutron).
2.4. Rappeler sans démonstration la relation liant la constante radioactive l et la période t_½.
ln2 = l t_½.
2.5. Donner l'expression de l'activité A de l'échantillon à une date t en fonction de A₀ et t_½.
A = A₀ exp (-lt) ; ln (A₀/A) = l t = ln2 t / t_½.
On pose x = t / t_½. ; A₀/A = 2^x.
2.6 Que vaut l'activité de l'échantillon d'iode 123 à 2t_½ soit un peu plus de 24 h après l'injection.
x = 2 ; A₀/A = 4 ; A = 0,25 A₀ = 0,25*7 ~1,8 MBq.
2.8. Donner la courbe représentant l'évolution de l'activité au cours du temps.

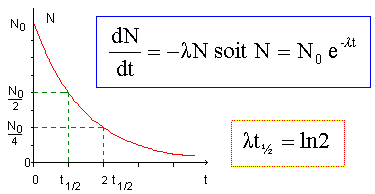
Electrostatique, électromagnétisme ( 3 / 20).
1. On place une charge ponctuelle q en un point O de l'espace. Donner l'expression du champ électrostatique créé par cette charge en un point M quelqonque de l'espace.

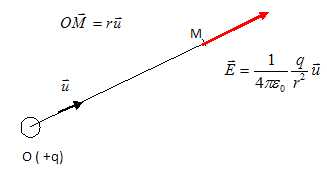
Pour une charge q négative, le champ électrostatique a le sens contraire à celui du schéma.
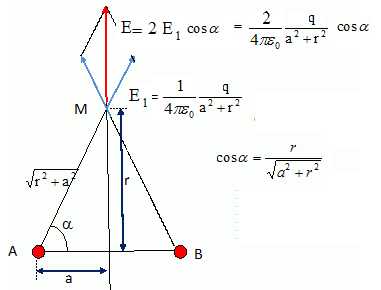
2. On onsidère deux charges ponctuelles identiques positives placées en deux points A et B distant de 2a. Soit M un point quelconque du plan médiateur du segment [AB] et situé à la distance r de ce segment.. Donner l'expression du champ électrostatique créé par ces deux charges en M en fonction de q, a, r et e₀.

3. Enoncer avec précision le théorème de Gauss.

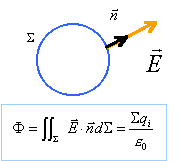
D'après le théorème de Gauss, le flux du vecteur champ électrique à travers la surface S est égal à la somme des charges situées à l'intérieur de S divisée par e₀.
4. On considère une charge Q répartie uniformément à l'intérieur d'une sphère de centre O et de rayon R.
a. Donner l'expression du champ électrostatique créé par cette distribution de charge en un point M de l'espace situé à la distance r du point O avec r > R.

Par raison de symétrie le champ est radial. On considère une sphère S , de centre O et de rayon r.

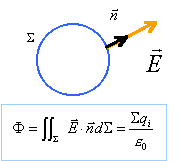
D'après le théorème de Gauss, le flux du vecteur champ électrique à travers la surface S est égal à la somme des charges situées à l'intérieur de S divisée par e₀.
F = E 4pr²= Q / e₀ d'où E = Q / (4pr²e₀).
b. En déduire l'expression dupotentiel électrostatique au point M en supposant qu'il est nul à l'infini.

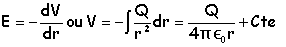; la constante d'intégration est nulle.

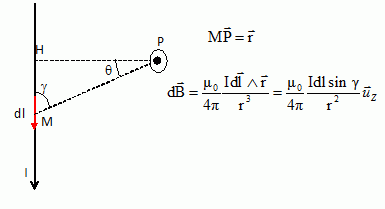
5. On considère un circuit électrique filiforme parcouru par un courant continu d'intensité I. En vous aidant d'un schéma clair, énoncer la loi de Biot et Savart donnant l'expression du champ magnétique élémentaire créé en un point M par l'élément de circuit dl autour du point P du circuit.

L'élément de courant Idl crée en P un champ magnétique élémentaire dB, perpendiculaire au plan formé par Idl et MP, orienté vers l'avant du plan.

6. On considère une spire circulaire de rayon r et de centre O parcourue par un courant d'intensité I. Déterminer l'expression du champmagnétique créé par la spire en un point M de son axe Oz.

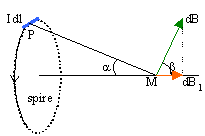
L'élément de courant Idl crée en M , le champ élémentaire dB, perpendiculaire à PM, de module :

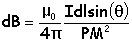
Idl et PM étant perpendiculaire sin(q)=1.
Par raison de symétrie le champ résultant sera porté par l'axe horizontal. La composante utile sera dBcos(b) = dBsin(a)
Pour tous les éléments Idl, l'angle a et PM sont les mêmes. L'intégration de dB sur toute la spire donne le module du champ résultant ( sin a = rayon r / PM )

.

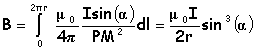
menu