Satellites
de Jupiter, étude d'un ressort, composition de mouvements.
Concours EMIA 2011.
école militaire interarmes
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Satellite de Jupiter ( 2 / 7).
1.1. Donner
l'expression vectorielle de la force d'interaction gravitationnelle
exercée par Jupiter sur un de ses satellites de masse m et situé à la
distance r du centre O de Jupiter
 .
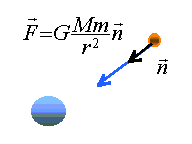1.2. Enoncer
le principe des actions réciproques ou troisième loi de Newton. Que
peut-on en déduire pour Jupiter et son satellite Europe ?
Interaction entre un objet A et un objet B : si un solide noté A exerce sur un solide noté B une force notée F A / B, alors B exerce sur A une force notée F B / A . Les deux forces associées à une même interaction sont toujours égales et opposées.
1.3.
Définir un mouvement circulaire et uniforme puis donner les
caractéristiques du vecteur accélération d'un point mobile qui subit un
telmouvement.
La trajectoire est un cercle de centre O et de rayon
R. La norme de la vitesse est constante. L'accélération est centripète,
de valeur aN = v2 / R.
1.4. Le mouvement
du satellite Europe est décrit dans un référentiel jupitérocentrique ;
par analogie avec le référentiel géocentrique, donner les
caractéristiques du référentiel jupiterocentrique. Le référentiel jupitérocentrique est construit à partir des centres de Jupiter et de trois étoiles lointaines qui paraissent fixes.
1.5. Montrer que si l'orbite du satellite Europe est circulaire, le mouvement de son centre d'inertie est uniforme
Le
vecteur vitesse du satellite, tangent au cercle, est constament
perpendiculaire à la force de gravitation centripète exercée par
Jupiter. Cette force ne travaille pas ; l'énergie cinétique du
satellite n'est pas modifiée et en conséquence la norme de son vecteur
vitesse reste constante.
1.6. Démontrer que, dans ces conditions, la vitesse du centre d'inertie du satellite Europe vérifie : v = [GM / r] ½ avec r rayon de l'orbite d'Europe et M masse de Jupiter.
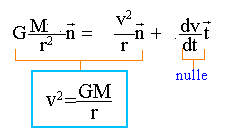
1.7. Démontrser que le rapport T2/r3 ne dépend que de G et de la masse de Jupiter. Quelle loi retrouve-t-on avec ce résultat ? ( T : période du satellite Europe ).
période : durée pour décrire la
circonférence à la vitesse v, norme constante.
2pr = vT
élever au carré,
puis remplacer v² par l'expression ci dessus.
4p² r² =GM / r T²
ou T² =4p² /(GM) r3. ( 3 ème loi de Kepler).
1.8. Estimer numériquement la masse de Jupiter.
T = 3,07 105 s ; r = 671 000 km.
T2 / r3 = (3,07 105)2 / (6,71 108)3 = 3,12 10-16.
M = 4*3,142 /(6,67 10-11 * 3,12 10-16)=1,9 1027 kg.
|
|
|
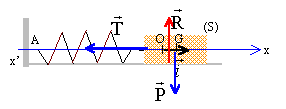
Etude d'un ressort ( 3 / 20).
Une
extrémité du ressort est attaché à un support vertical fixe au point A
et à l'autre extrémité du ressort, on fixe un solide S de masse m ; on
guide ce solide par l'intermédiaire d'une tige horizontale Ax.
L'anscisse
x du centre d'inertie G du solide S est mesurée par rapport à la
position O de G au repos, on a donc x =0 à l'équilibre. On écarte le
solide S de sa position d'équilibre jusqu'à ce que l'abscisse de G soit
x = Xm puis on le lâche sans vitesse initiale à la date t = 0.
m = 100 kg ; k = 4000 N m-1 ; Xm = 0,10 m.
A. On suppose que le mouvement s'effectue sans frottement.
2.1. En vous aidant d'un schéma faire l'inventaire des forces appliquées au système dans le référentiel du laboratoire.
La masse est soumise à son poids, verticale vers le bas,valeur mg ;
- à l'action du support, verticale vers le haut, opposée au poids ;
- à la force de rappel exercée par le ressort, horizontale, dirigée vers la position d'équilibre, valeur k x.
2.2. Etablir l'équation différentielle du mouvement de G.
Ecrire la seconde loi de Newton :
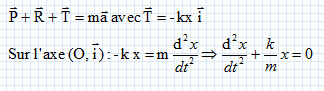
2.3. Comment appelle-t-on un oscillateur vérifiant ce type d'équation différentielle ?
Oscillateur harmonique.
2.4. En déduire l'équation horaire du mouvement de G.
x(t) = Xm cos ( wt) avec w2 = k / m.
2.5.
Déterminer l'expression littérale de la période propre T0 de cet oscillateur.
w2 = 4 p2/T20
d'où T0 =2 p (m/k)½.
2.6 Calculer T0.
T0 = 2 *3,14 (100 / 4000)½ =0,993 s.
2.7.
Donner l'expression de l'énergie potentielle associée à la force de rappel du ressort.
Ep = ½kx2.
2.8.
Définir l'énergie mécanique du système solide-ressort puis établir son
expression en foncton des données. Comment évolue cette énergie au
cours du temps ?
L'énergie mécanique est la somme de l'énergie
potentielle et de l'énergie cinétique. En absence de frottement, elle
est constante et vaut E = ½kXm2.
2.9 et 10 . Décrire un protocole opératoire permettant de déterminer K.
Pour différentes masses, pour la même amplitude, déterminer la période T0.
k = 4p2m / T02.
B. Prise en compte du frottement fluide.
11. Etablir une nouvelle équation différentielle du mouvement.
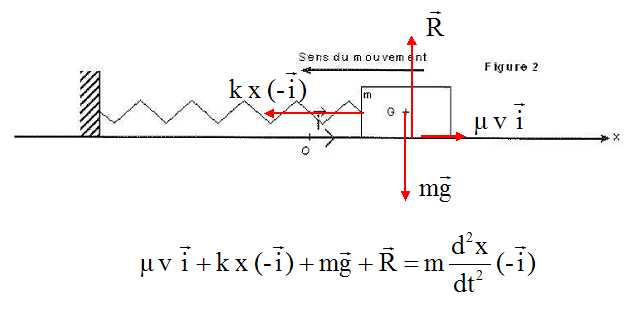
Lorsque la masse se déplace vers la gauche, la vitesse est négative.
-µ dx/dt -kx = md2x/dt2.
d2x/dt2 + µ / m dx/dt + k / m x = 0.
12.
Cette équation est formellement identique à celle obtenue lors de
l'étude des oscillations électriques. De quel type de circuit
électrique s'agi-il ?
Circuit RLC série.
13. Si le frottement est faible, quel sera le type de mouvement observé ?
Mouvement pseudo-périodique.
14. Tracer l'allure du graphe x= x(t) pour un frottement faible en faisant apparaître sur le schéma la période propre T0 de l'oscillateur.
15.
Quels sont les deux autres régimes d'oscillations que l'on peut
observer en modifiant le frottement ? Tracer l'allure des courbes x(t)
dans les deux cas.
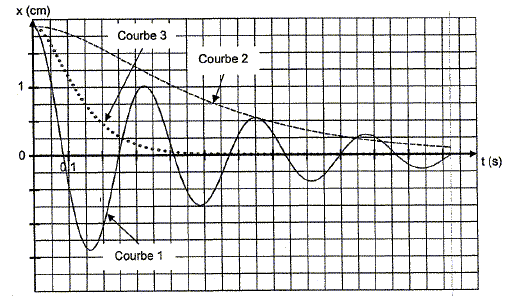
Courbe 1 : régime pseudo-périodique ; courbe 2 : régime critique ; courbe 3 régime apériodique.
|
|
