L'univers du
térahertz, ou rayons T.
Bac S Polynésie 2017 .
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
|
|
|
|
Les
fréquences des rayons T sont comprises entre 0,1 THz et 30 THz. 1 THz =
10 12 Hz.
1. Térahertz et scanner..
De par leur nature même, à la frontière de l'optique et des
micro-ondes, les propriétés des ondes T cumulent les avantages des deux
mondes.
- elles peuvent pénétrer certains matériaux opaques au rayonnement
visible tels que le carton, les tissus, le bois ou les matières
plastiques.
- elles interagissent peu avec la matière, ce qui permet de les
utiliser dans des applications d'imagerie pénétrante sans toutefois
présenter de danger pour les organismes vivants.
· 1.1.
Certains rayonnements sont dits ionisants. Leur énergie supérieure à 10
eV, est suffisante pour transformer les atomes en ions. Ces
rayonnements ionisants peuvent être nocifs pour les organismes vivants
si la quantité d'énergie reçue est trop élevée.
1.1.1. Calculer
l'énergie en eV :
- d'un proton associé à un rayonnement X de fréquence égale à 1,0
10 17 Hz.
E = h n = 6,63 10 -34
x1,0 10 17=6,63 10 -17 J
6,63 10 -17 / (1,60 10 -19) ~ 4,1 102 eV.
- d'un proton
associé à un rayonnement T de fréquence égale à 1,5 1012 Hz.
E = h n = 6,63 10-34
x1,5 1012=9,945 10-22 J
9,945 10-22 / (1,60 10-19) ~6,2 10-3 eV.
1 .1.2. Comparer l'impact sur les
organismes vivants d'un scanner à rayons X et d'un scanner à rayons T.
Justifier.
L'énergie des rayons X est supérieure à 10 eV. Ce rayonnement est
suffisamment énergétique pour transformer les atomes en ions, donc
dangereux pour les organismes vivants..
L'énergie des
rayons T est très inférieure à 10 eV. Ce
rayonnement n'est pas suffisamment énergétique pour transformer les
atomes en
ions, donc inoffensif pour les organismes vivants.
1.2. Le pouvoir de
résolution d'un système d'observation, est sa capacité à séparer deux
points distincts pour qu'ils soient correctement discernés par
l'observateur. Il est lié à la diffraction de l'onde, de longueur
d'onde l lorsque
l'onde traverse le milieu d'observation.
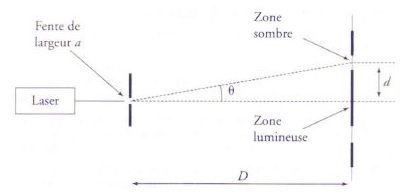
1.2.1. On éclaire
une fente de largeur a par un laser de longueur d'onde l.
Rappeler l'expression
reliant l'angle q
aux grandeurs a et l.
q = l /a.
|
....
.....
|
1.1.2.
Cette fente est maintenant éclairée par deux faisceaux laser faisant un
angle a avec
l'axe de la fente. On suppose que l'ouverture q du faisceau liée à la
diffraction a la même expression que lorsque l'axe du faisceau arrive
perpendiculairement à la fente.
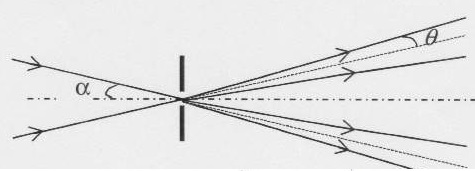
Montrer que si l'angle a
est petit, il est impossible de séparer les deux faisceaux à la sortie
de la fente. Donner l'expression de la valeur limite de a.
Si a < q, les rayons se chevauchent
à la sortie de la fente.
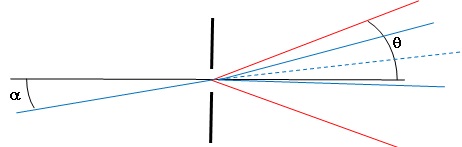
a > q, les rayons ne se
chevauchent pas à la sortie de la fente.
La valeur limite de a
est q.
1.3. Plus le
diamètre D de lobjectif de la caméra qui équipe le scanner est grand,
plus les détails observés sont petits. Un objet étant positionné à une
distance L de la caméra, on distingue deux points A et B de l'objet
séparés d'une distance d si le diamètre Dmin de l'objectif
de la caméra est au minimum de :
Dmini = 1,22 l
L / d.
1.3.1. Pour un
objet situé à 12 cm de la caméra térahertz, sensible au rayonnement de
fréquence égale à 1,5 THz, montrer que deux points séparés de 0,20 mm
ne peuvent pas être distingués avec un objectif de diamètre 10 cm.
l = c / f = 3,0 108
/ (1,5 1012) = 2,0 10-4 m.
d = 1,22 l L / D = 1,22 x 2 10-4
x0,12 / 0,10 =2,93 10-4 m ~ 0,29 mm.
Cette valeur est supérieure à 0,20 mm.
Deux points séparés de 0,29
mm peuvent être distingués avec un objectif de diamètre 10
cm.
Deux points séparés de 0,20
mm ne peuvent pas être distingués avec un objectif de
diamètre 10 cm.
1.3.2. Comment
modifier la valeur de la fréquence des ondes T afin de visualiser
distinctement ces deus points ?
d est proportionnelle à la longueur d'onde.
La longueur d'onde est inversement proportionnelle à la fréquence.
La
distance d est inversement proportionnelle à la fréquence.
Pour diminuer d il faut augmenter la
fréquence.
|
|
|
2.T
érahertz et étude de l'univers.
La naissance de l'univers s'est accompagnée de l'émission d'un intense
rayonnement électromagnétique. Ce rayonnement nous parvient, atténué,
après avoir cheminé pendant des milliards d'années dans l'espace.
Provenant de toutes les directions de l'univers, ce rayonnement fossile
apparaît homogène et se comporte comme le rayonnement d'un corps noir à
la température de 3 K.
Loi de Wien : lmax
T = 2,90 10-3 m K.
lmax
longueur d'onde majoritairement émise ( exprimée en m) dans le spectre
d'émission d'un corps noir porté à la température T ( K).
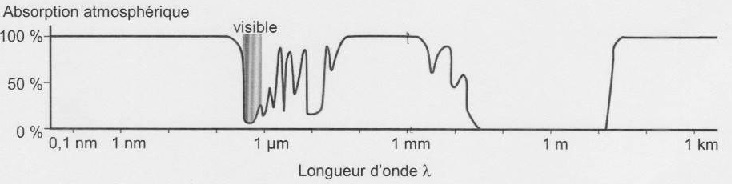
Absorption de l'atmosphère en fonction de la longueur d'onde de l'onde
électromagnétique.
|
|
|
|
2.1.
Montrer que le rayonnement fossile peut être
considéré comme un rayonnement térahertz.
lmax
= 2,90 10-3 / T = 2,90 10-3 / 3 ~9,67 10-4
m = 0,97 mm.
Fréquence correspondante : f = c / lmax = 3,0 108
/ (9,67 10-4) ~3,1 1011 Hz = 0,31 THz.
Or les fréquences des rayons T sont comprises
entre 0,1 THz et 30 THz.
Le rayonnement fossile peut être considéré comme un
rayonnement térahertz.
2.2. Le rayonnement
fossile peut-il être directement étudié avec des instruments au sol ou
nécessite -t-il l'utilisation d'un satellite ? Justifier.
L'atmosphère absorbetotalement le rayonnement fossile de longueur
d'onde voisine de 1 mm.
Le rayonnement fossile ne peu pas être directement étudié avec des
instruments au sol ; son étude nécessite l'utilisation d'un
satellite.
|
|