Sons et lumières,
bac
S Métropole 2017 .
|
|
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
|
|
|
|
Pour obtenir un feu d'artifice qui
produit son, lumière et fumée, on procède à l’éclatement d’une pièce
pyrotechnique. Bien que produisant des effets différents, toutes ces
pièces sont conçues selon le même principe. Un dispositif permet de
projeter la pièce pyrotechnique vers le haut. Une fois que ce
projectile a atteint la hauteur prévue par l’artificier, il éclate,
créant l’effet « son et lumière » souhaité. Le but de cet exercice est
d’étudier la couleur observée, la trajectoire du projectile et le son
émis.
1. Tout en couleur.
Les feux d’artifice émettent de la lumière. Les phénomènes mis en jeu
sont notamment l’incandescence et l’émission atomique. Il y a tout
d’abord l’incandescence des particules d’oxyde métallique, formées lors
de la combustion, qui va du « blanc rouge » (aux alentours de 1 000 °C)
jusqu’au blanc éblouissant (vers 3 000 °C). Pour l’émission atomique,
les électrons de l’atome sont excités thermiquement, ce qui leur permet
de passer du niveau d’énergie fondamental à un niveau d’énergie
supérieur ; au cours de leur retour vers le niveau d’énergie
fondamental, l’énergie qu’ils avaient absorbée est émise sous forme de
photons dont la longueur d’onde est caractéristique de l’atome.
D’après :
http://www.ambafrance-cn.org/Feux-d-artifice-histoire-et-technologie
1.1. Le texte fait
référence à deux processus d’émission de lumière. Citer chacun de ces
processus et préciser, dans chaque cas, si le spectre de la lumière
émise est un spectre de raies ou un spectre continu.
Incandescence : spectre continu du blanc rouge au blanc éblouissant.
Emission atomique : spectre de raies caractéristiques de l'élément
chimique. Les niveaux d'énergie de l'atome sont quantifiés.
Le « crackling R100 » est principalement composé de strontium. Les
photons émis par le strontium sont responsables de la couleur perçue
lors de l’éclatement du « crackling R100 ». Le tableau ci-dessous
regroupe les énergies des photons émis par le strontium :
Photon 1, énergie 1,753 eV ; photon 2 , énergie 1,802 eV ; photon 3,
énergie 1,825 eV.
1.2. Déterminer la
couleur perçue lors de l’émission du photon 3.
E = 1,825 x1,6 10-19 = 2,92 10-19 J.
l = h
c / E = 6,63 10-34 x 3,0 108 / (2,92 10-19)
~6,8 10-7 m ~0,68 µm.
Le domaine du rouge s'étend de
0,625 à 0,78 µm.
1.3. Sans effectuer
de calcul supplémentaire, montrer que l’émission de ces trois photons
permet d’expliquer la couleur de la lumière émise par le « crackling
R100 ».
La couleur de la lumière
émise par le « crackling R100 » est un rouge intense.
Les énergies des photons 1 et 2 sont légèrement inférieures à celle du
photon 3. Or, énergie et longueur d'onde sont inversement
proportionnelles L'émission des photons 1 et 2 se situe donc dans
le rouge.
|
....
.....
|
2. Étude des trajectoires des pièces
pyrotechniques.
On s’intéresse au mouvement de la pièce pyrotechnique jusqu’à son
éclatement dans un référentiel terrestre supposé galiléen muni d’un
repère (Ox,Oy). On étudie le mouvement d’un point M de la pièce «
crackling R100 ». On prend l’instant du lancement comme origine des
temps t = 0 s.
À cet instant, le vecteur vitesse initiale V0 de M fait un
angle a= 80° par
rapport à l’horizontal.
2.1. Donner les
expressions littérales des coordonnées du vecteur vitesse initiale en
fonction de V0 et a.
V0 x = V0 cos a ; V0 y = V0
sin a. ( l'axe
vertical est orienté vers le haut ).
2.2. Montrer que,
si on néglige toute action de l’air, le vecteur accélération de M est
égal au vecteur champ de pesanteur dès que le projectile est lancé.
Le projectile est en chute libre, il n'est soumis qu'à son poids.
La seconde loi de Newton conduit à : ax = 0 ; ay
= -g.
2.3. Montrer alors
que les équations horaires du mouvement de M sont :
xM(t) = 12,1t et yM(t) = - 4,91t2 +
68,4t en exprimant xM(t) et yM(t) en mètres et le
temps « t » en secondes.
V0 = 250 km /h soit 250 / 3,6 = 69,4 m /s.
La vitesse est une primitive de l'accélération :
vx(t) = V0 cos a =69,4 x cos 80 ~12,1 m/s.
vy(t) = -gt +V0
sin a = -9,81
t+69,4 x sin 80 ~ -9,81 t +68,4.
La position est une primitive de la vitesse et la position initiale est
l'origine du repère.
xM(t) = 12,1 t ; yM(t) = -0,5 x9,81 t2
+68,4 t = - 4,91t2
+ 68,4t.
2.4. Dans le cadre
de ce modèle, déterminer, à l’aide des équations horaires, l’altitude
théorique atteinte par le projectile à t = 3,2 s.
y = -4,91 x3,22 +68,4 x3,2 ~168 ~1,7 102 m.
2.5. Sachant que
l’éclatement se produit lors de la montée, expliquer l’écart entre
cette valeur et celle annoncée par le constructeur ( 120 m).
L'altitude annonée est inférieure à l'altitude du modèle de la chute
libre. Les frottements doivent être pris en compte.
|
|
|
3.
Le « marron d’air »
Au début et à la fin de chaque feu d’artifice, les
artificiers
utilisent une pièce pyrotechnique appelée « marron d’air » pour obtenir
une détonation brève et puissante. Désireux de l’envoyer le plus haut
possible, ils effectuent un tir vertical avec une vitesse initiale vi.
Par la suite, on suppose que la pièce n’éclate pas avant d’atteindre sa
hauteur maximale h.
3.1. Dans
l’hypothèse où l’énergie mécanique de la pièce pyrotechnique se
conserve, montrer que la hauteur maximale h atteinte par cette pièce
est donnée par la relation : h =vi2
/ ( 2g).
Energie mécanique initiale : ½mvi2.
Energie mécanique finale : mgh.
Conservation de l'énergie mécanique : ½mvi2 = mgh.
vi2 = 2gh ; h =vi2
/ ( 2g).
3.2. Déterminer la
valeur de la hauteur maximale atteinte h.
vi = 200 km /h soit 200 / 3,6 ~55,55 m /s.
h = 55.552 / (2x9,81) = 157,3 ~157 m.
|
|
|
|
En
réalité, arrivé à une hauteur H de 70 m, le « marron d’air » éclate au
point E et le son émis se propage dans toutes les directions de
l’espace. Un artificier A se trouve à la distance ℓ = 95 m recommandée
par le constructeur du point de tir T du « marron d’air ».
3.3. Doit-on
recommander à l’artificier le port d’un dispositif de protection
auditive (casque, bouchons d’oreille,…) ? Justifier par un calcul.
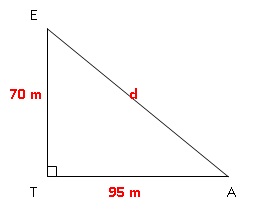
d2 = 952 +702 = 13925 ; d =118 m.
Au cours de la propagation d’une onde et en l’absence d’atténuation, le
niveau d’intensité sonore L diminue
avec la distance d à la source S suivant la formule :
L2 = L1 + 20.log (d1 / d2).
où L2 est le niveau d’intensité sonore mesuré à la distance d2
de la source et L1 le niveau d’intensité sonore mesuré à la
distance d1 de la source.
Niveau d’intensité sonore estimé à 15 m du point d’éclatement : 120 dB.
L2 = 120 +20 log(15 /118) =102 ~1,0 102 dB.
Ce niveau est difficilement suportable.
Un dispositif de protection auditive (casque, bouchons d’oreille ) est
nécessaire.
|
|