Interférences de
molécules,
bac
S Métropole 09 /2017 .
|
|
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
|
|
|
|
En
1905, Einstein décrit l’onde lumineuse comme un flux de particules sans
masse : les photons. Par la suite, en 1924, Louis de Broglie a l’idée
d’associer une onde à une particule de matière en mouvement ; on a
depuis observé des interférences de particules (électrons, atomes,
molécules …).
L’objectif de cet exercice est d’étudier, dans une première partie, les
interférences lumineuses obtenues à l’aide d’un réseau et, dans une
deuxième partie, un dispositif expérimental d’interférences utilisant
des molécules de phtalocyanine.
Données :
- constante d’Avogadro : N A = 6,02 × 10 23 mol -1
;
- constante de Planck : h = 6,63 × 10 -34 m 2.kg.s -1
;
- intensité du champ de pesanteur : g = 9,81 m.s -2 ;
- masse molaire moléculaire de la phtalocyanine : M = 514,5 g.mol -1.
1. Interférences d’ondes
lumineuses par un réseau.
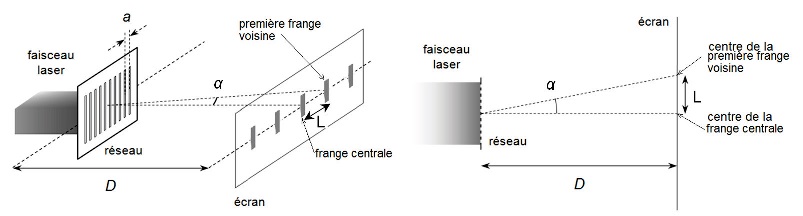
On considère un réseau constitué d’une lame dans laquelle est gravée
une série de fentes parallèles régulièrement espacées. La distance
régulière entre les fentes, notée « a », est appelée « pas du réseau ».
Lorsqu’on éclaire ce réseau avec un faisceau laser monochromatique de
longueur d’onde λ, les ondes lumineuses diffractées par les différentes
fentes se superposent sur un écran. En certains points de l’écran, les
interférences sont constructives ; on observe alors sur l’écran une
figure d’interférences constituée de franges lumineuses régulièrement
espacées.
On note L la distance entre le centre de la frange centrale et le
centre de sa première voisine
1.1. À quelle
condition obtient-on, en un point de l’écran, un phénomène
d’interférences constructives lorsque deux ondes lumineuses cohérentes
interfèrent ?
La différence de marche entre les deux ondes qui interfèrent doit être
égale à un multiple de leur longueur d'onde.
1.2. Si l’angle α,
indiqué sur les figures, est « petit » et exprimé en radians, on peut
faire les approximations suivantes : sin α ≈ α et tan α ≈ α. Montrer
dans ce cas que L =l
D/a. (relation 1).
D'une part tan a ~a = L / D ; d'autre part a = l / a.
Par suite : L =l D/a.
1.3.
On remplace la source laser par une source de lumière blanche. On
observe une frange centrale de couleur blanche et des franges latérales
colorées. Sur la première frange voisine de la frange centrale, donner
l’ordre dans lequel les couleurs bleu et rouge sont observées, en
partant du centre de la tâche centrale. On argumentera sans calcul en
utilisant la relation 1.
lbleu
< lrouge
; de plus L est proportionnelle à l.
Le bleu est plus proche que le rouge du centre de la tache centrale
|
....
.....
|
2. Interférences de molécules de
phtalocyanine
En mai 2012, une équipe de scientifiques a publié un article dans le
magazine « Nature Nanotechnology ».
Cet article décrit une expérience qui a permis d’observer un phénomène
d’interférences obtenues à partir
d’un faisceau de molécules de phtalocyanine. On donne ci-dessous un
descriptif simplifié de l’expérience.
Les molécules de l’échantillon de phtalocyanine sont vaporisées pour
former un faisceau horizontal de molécules se déplaçant suivant l’axe
Ox. La vitesse des molécules varie de quelques dizaines à quelques
centaines de mètres par seconde. Après avoir traversé la fente, les
molécules se dirigent vers le réseau qu’elles traversent avant de se
déposer sur un écran transparent. Éclairées par une lumière adéquate,
les molécules deviennent fluorescentes et une figure d’interférences
peut alors être observée à l’aide d’une caméra.
2.1. Faisceau de molécules
de phtalocyanine entre la fente et le réseau.
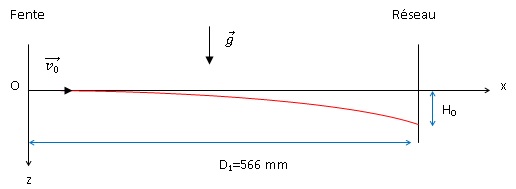
On s’intéresse, dans cette partie, au mouvement de chute dans le champ
de pesanteur terrestre d’une molécule de phtalocyanine de masse m. La
molécule se déplace dans un vide poussé et n’est donc soumise qu’à son
poids. Elle sort de la fente horizontalement avec une vitesse initiale v0.
L’étude du mouvement est effectuée dans le référentiel du laboratoire,
considéré comme galiléen. L’axe Oz est vertical, orienté vers le bas.
La date t = 0 est prise au moment où la molécule est au point O.
2.1.1.
Démontrer que les équations horaires du mouvement de la molécule de
phtalocyanine dans le repère (Ox, Oz) sont de la forme : x (t ) =v t et
z (t ) =½ gt 2.
La seconde loi de Newton appliquée à cette chute libre verticale
conduit à : ax=0 ; az = g.
La vitesse est une primitive de l'accélération et la vitesse initiale
est horizontale.
vx = v0 ; vz = gt.
La position est une primitive de la vitesse et la position initiale est
l'origine du repère.
x = v0t ; z = ½gt2.
2.1.2. Exprimer la
date t1 à laquelle la molécule atteint le réseau en fonction
de v0 et D1, ( distance fente réseau). En déduire
l’expression de la distance H0 ( ordonnée de la position à
l'abscisse D1) en fonction de g, D1 et v0,
puis calculer la valeur de cette distance pour une vitesse initiale v0
= 1,5 × 102 m.s-1.
t1 = D1 / v0 ; H0 = ½gt12
= ½g( D1 / v0)2.
H0 =0,5
x9,81(0,566 / 150)2=6,7 10-5 m.
2.1.3. Indiquer, en le justifiant
brièvement, comment évolue la distance H0 lorsque la vitesse
initiale v0 de la molécule augmente.
H0 est inversement proportionnel à v02.
H0 diminue si v0 croït.
|
|
|
2.2. Figure d’interférences observée.
Après une durée d’enregistrement suffisante, on obtient à l’aide d’une
caméra une figure d’interférences sur laquelle on observe des franges
s’écartant vers le bas. On a tracé la courbe expérimentale qui donne
les variations de l’intensité lumineuse de fluorescence au voisinage de
la droite (Δ) correspondant aux molécules de vitesse v0 =
1,5 × 102 m.s-1.
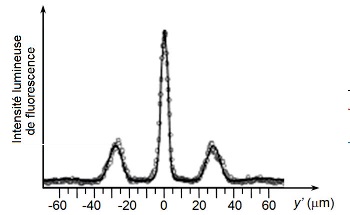
D’après l’article “Real-time single-molecule imaging of quantum
interference” Nature Nanotechnology - mai 2012
|
|
|
|
2.2.1. Quel caractère de la matière
est mis en évidence par cette figure d’interférences ?
Les interférences mettent en évidence le caractère ondulatoire de ce
faisceau de particules.
2.2.2. Vérifier, à
l’aide des données fournies en début d’exercice, que la masse d’une
molécule de phtalocyanine est m = 8,55×10-25 kg.
M / NA =0,5145 / (6,02 1023) =8,55 10-25
kg.
2.2.3. On considère
une molécule de phtalocyanine en mouvement à la vitesse v0 =
1,5×102 m.s-1.
Calculer la valeur de la longueur d’onde de de Broglie λDB
associée à cette molécule.
l = h
/ (mv0) =6,63 10-34 /(8,55 10-25 x1,5
102) =5,17 10-12 ~5,2 10-12 m.
2.2.4. Indiquer, en
le justifiant brièvement, comment évolue la longueur d’onde de de
Broglie d’une molécule de phtalocyanine lorsque sa vitesse initiale v0
augmente.
La longueur d'onde est inversement proportionnelle à la vitesse. La
longueur d'onde diminue si la vitesse initiale croît.
2.2.5. On note L0
la distance séparant le centre de la frange centrale du centre de l’une
des deux premières franges voisines pour des molécules de phtalocyanine
de vitesse initiale v0 = 1,5 × 102 m.s-1.
Comparer la valeur obtenue pour L0 à partir de la courbe
expérimentale et la valeur calculée à partir de la relation 1 (question
1.2.) appliquée au dispositif expérimental). a = 100 nm ; D2
= 564 mm ( distance réseau - écran ).
A partir de la courbe expérimentale L0 = 30 µm.
L0
=l D2 / a=.5,17 10-12
x0,564 /(1,00 10-7)=2,91 10-5 m = 29,1 µm.
Ecart relatif : ( 30 -29,1) / 30 = 0,03 ( 3 %). Les deux valeurs sont
compatibles.
2.2.6.
Expliquer, à l’aide d’un raisonnement qualitatif (sans calcul),
pourquoi les franges s’écartent vers le bas de la figure
d’interférences.
La vitesse des molécules varie de quelques dizaines à quelques
centaines de mètres par seconde.
Aux faibles vitesses, la longueur d'onde et en conséquence L,
augmentent.
Aux grandes vitesses, la longueur d'onde et en conséquence L, diminuent.
|
|