Mesure de vitesse, le klomètre lancé
bac S Nlle Calédonie 2017.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.



.
.


Le kilomètre lancé (K.L.) ou ski de vitesse est une discipline dans laquelle l'objectif est d'atteindre la plus grande vitesse possible sur une piste. Il ne se passe pas une année sans qu'un nouveau record ne soitétabli.
252,632 kmlh : nouveau record de vitesse pour le skieur Simone Origone
« Impossible, 252,632 km/h ? Un homme ne peut pas se déplacer aussi vite, quelqu'un a dû appuyer sur « avance rapide ». Et pourtant. C'est bien la vitesse atteinte vendredi 3 avril par Simone Origone qui, pour y parvenir, s'est servi d'un instrument complexe: une paire de skis. Et d'un moteur surpuissant : la gravité. L'Italien de 35 ans a battu son propre record du monde de vitesse à ski (252,454 km/h), réussi le 31 mars 2014. »
D'après un article du site lemonde.fr du 3 avril 2015

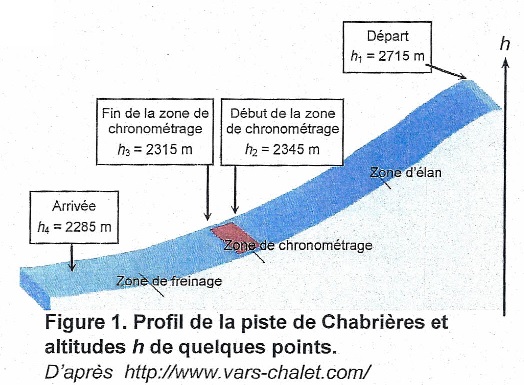
Comme toutes les pistes de ski de vitesse, la piste de Chabrières comporte trois zones: une zone d'élan, une zone de chronométrage
et une zone de freinage. Le départ est situé à une altitude h1 = 2715 m. Le skieur accélère sur une distance de 450 m avant d'arriver
dans la zone de chronométrage où l'on mesure le temps mis pour parcourir une distance D = 100 m. À la sortie de cette zone
de chronométrage, le skieur décélère progressivement dans la zone de freinage.

Données : » intensité du champ de pesanteur terrestre: 9 = 9,81 rn.s-2: » masse du skieur avec son équipement: M = 110 kg.
Le système est composé du skieur et de son équipement; l'étude est conduite dans le référentiel terrestre que l'on supposera galiléen.
1. Vitesse maximale
1.1. Dans l'article, il est dit que le skieur utilise « un moteur surpuissant : la gravité ». Justifier qu'au cours de la descente le travail du poids du skieur est "moteur ", c'est-à-dire positif.

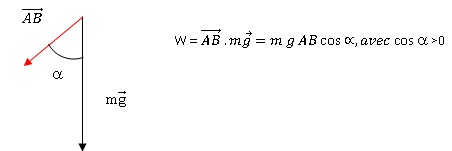1.2. En considérant que la valeur de la vitesse du skieur au départ est nulle et que l'énergie mécanique du système se conserve, montrer que la valeur de la vitesse atteinte par le skieur au début de la zone de chronométrage est égale à 85 rn.s-1.
Energie mécanique initiale : mg h1 .
Energie mécanique en début de la zone de chronométrage : ½mv2+mgh2.
Conservation de l'énergie mécanique.
½mv2 +mgh2.= mgh1 ; v =(2g(h1-h2))½=(2x9,81(2715-2345))½=85,2 m s-1.
1.3. Comparer la valeur de cette vitesse à celle réellement atteinte par S.Origone en avril 2015. Proposer une explication de la différence observée.
Vitesse réelle : 252,632 /3,6 =70,17  m s-1.
Il faut tenir compte des frootement sur les couches d'air et au contact du sol.
2. Les frottements de l'air
L'expression suivante permet de calculer la valeur Fair de la force de frottement de l'air s'exerçant sur un skieur en mouvement:
Fair = 0,5  rair  S  k v2 ;
Avec :
» rair la masse volumique de l'air en kg.m-3 ; » v la vitesse du skieur en rn.s-1 ;
» S (en m2) la surface occupée par le skieur dans un plan perpendiculaire à son déplacement;
» k le coefficient de trainée qui dépend de la posture du skieur et de son équipement.
Au cours de son mouvement dans la zone d'élan, le skieur peut adopter différentes postures. À chacune d'elles correspond une valeur du produit S x k. Le document ci-dessous donne les valeurs du produit S x k, en unité de base du système international, pour différentes postures d'un skieur.

2.1. Montrer que k est une grandeur sans unité. Quelle sera alors l'unité du produit S x k?
k =2 Fair /(  rair  S   v2).
Fair est une force exprimée en newton soit en kg m s-2.
  rair  S   v2 s'exprime en kg m-3 m2 (m s-1)2 soit kg m s-2.
k est donc sans dimension et kS2 s'exprime en m2.


2.2. Si on considère que le coefficient de trainée k reste constant entre les deux positions, proposer une explication qualitative à la diminution du produit S x k observée pour les postures 1 et 2.
Dans la posture 1, S est plus grande que dans la posture 2 ( skieur plus regroupé sur lui même )..
En vous basant sur le document ci-dessus, évaluer la valeur de la surface S pour la posture 2 et donner un ordre de grandeur de la valeur de k.
S oeut être assimilée à la surface d'un rectangle de 0,8 m de haut et 0,38 m de large.
S ~0,3 m2 ; k =0,159 /0,3 ~ 0,5.
2.3. Parmi les postures proposées, indiquer celle qui permettra au skieur d'atteindre la plus grande vitesse au début de la zone de chronométrage. Justifier.
La vitesse maximale est obtenue dans le cas où la résistance de l'air est la plus faible possible. Il faut donc que kS soit le plus faible ( posture n°2).
2.4. Pour une posture donnée, expliquer comment évolue la valeur de la force de frottement de l'air Fair lorsque la vitesse du skieur augmente. Justifier.
Pour une posture donnée kS est constant. Fair est proportionnelle au carré de la vitesse. Fair croît avec le carré de la vitesse.
3. Mesure des records et métrologie
3.1. Calculer la durée tc du passage du skieur dans la zone de chronométrage de distance D.
La vitesse étant supposée constante dans la zone de chronométrage, tc = D / v = 100 / 85 = 1,176 s ~1,2 s.
3.2. Donner deux sources d'erreurs possibles pour la mesure de vitesse d'un skieur de kilomètre lancé.
Erreur sur la durée tc, erreur sur la distance D de chronométrage.
3.3. Justifier à l'aide du texte d'introduction pourquoi il est nécessaire de faire des mesures précises pour distinguer les différents records de vitesse.
Les vitesses sont exprimées avec 3 chiffres significatifs.
La différence de vitesse entre les deux derniers reccords est très faible  252,632 -252,354 = 0,278 km /h.
Les mesures de durée ainsi que celle de la distance D doivent être très précises.
3.4. Estimer la précision relative sur la mesure de la vitesse du skieur.
Les vitesses sont exprimées avec 3 chiffres significatifs.
Dv = 10-3 km /h ; v = 252,632 km/h ; Dv / v ~4 10-6.



  

menu