Le
water jump est une activité en plein essor. Le principe en est simple :
un skieur muni d’une combinaison glisse sur un toboggan préalablement
mouillé et terminé par un tremplin. Puis, à la sortie de ce dernier, il
effectue un saut en chute libre avant de
terminer sa course dans un plan d’eau.
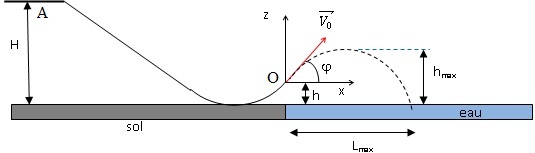
Masse du skieur et de son équipement : m = 73 kg.
Il existe quatre tremplins dont les caractéristiques sont données dans
le tableau ci-dessous.
|
Hauteur
H
|
hauteur
h
|
angle
j
|
Tremplin
débutant
|
H1
= 3,5 m
|
h1
= 0,85 m
|
j1 = 20°
|
Tremplin
médian
|
H2
= 7,0 m |
h1
= 0,85 m |
j1 = 20° |
Tremplin
averti
|
H1
= 3,5 m |
h2
= 1,7 m |
j2 = 45° |
Tremplin
expert
|
H2
= 7,0 m |
h2
= 1,7 m |
j2 = 45° |
Le sol horizontal
est choisi comme origine de l’énergie potentielle de pesanteur.
Les dimensions du skieur étant faibles devant toutes les autres
utilisées dans le problème, il est modélisé par un point matériel. Les
frottements seront négligés dans toutes les étapes du mouvement.
L’étude est effectuée dans le référentiel terrestre supposé galiléen.
L'origine des énergies potentielles est choisie au niveau du sol.
Partie 1 : étude
énergétique du skieur sur le tremplin
1.1. Par des
mesures, estimer l’angle φ du tremplin photographié de profil.

Pour un angle de 45° ( tan 45 = 1) la hauteur du tremplin est égale à
la longueur de sa base.
hauteur mesurée : ~1,8 cm ; base mesurée ~5 cm; tan
j =1,8 / 5 ~0,36 ;
j~
20°.
1.2. S’agit-il du
tremplin débutant ou expert ?
Il s'agit du tremplin
débutant.
1.3. Quel est
l’intérêt d’humidifier le toboggan avant son utilisation ?
Le film d'eau améliore la glisse et diminue les frottements.
Utilisation du tremplin débutant
1.4. Exprimer
l’énergie mécanique E
mA du skieur à l’instant initial,
lorsqu’il s’élance du point A sans vitesse initiale.
L'énergie mécanique est sous forme potentielle, la vitesse initiale
étant nulle.
E
mA =
mgH.
1.5. Déterminer la
relation entre l’énergie mécanique E
mO au moment où
il quitte la piste en O et l’énergie mécanique E
mA.
Justifier votre
réponse.
Les frottements sont négligés. Le skieur est soumis à son poids et à
l'action du support, perpendiculaire au support.
L'énergie mécanique se conserve.
EmA =
EmO.
1.6. Déterminer la
vitesse du skieur au point O.
E
mO = mgh +½mv
O2= mgH ;
vO2=2g(H-h)
; vO = (2g(H-h))½ = (2 x 9,81 (3,5-0,85))½=7,21
~7,2 m /s.