Les sciences au service de la performance sportive. Bac S Amérique du nord 2017 . En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . Les sciences permettent d’analyser et de comprendre les performances des athlètes. Les scientifiques s’intéressent à la physique, à la biomécanique, à la physiologie et aux transformations chimiques intervenant lors des pratiques sportives. Dans cet exercice, on s’intéresse à la pratique d’un sport d’endurance : le cyclisme. L’exercice est constitué de deux parties indépendantes : - partie 1 : Calcul des puissances développées par les cyclistes ; - partie 2 : Étude de la physiologie de l’effort et régulation du pH sanguin. Partie 1 : Calcul des puissances développées par les cyclistes. Afin d’améliorer les performances des cyclistes, on utilise une méthode de calcul indirect des puissances qu’ils fournissent lors d’un effort. Cette méthode s’appuie sur un modèle qu’il faut valider en le comparant avec les données mesurées en temps réel pendant l’effort grâce à un capteur (boitier SRM) placé sur le pédalier. 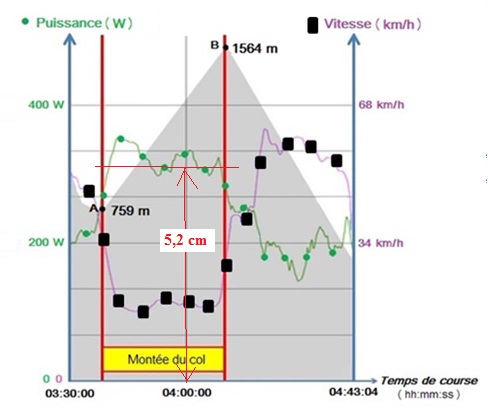Dans cette partie, on s’intéresse à l’ascension par un cycliste du col pyrénéen de la Hourquette d’Ancizan. Il effectue cette montée, longue de 10,4 km, en 31 min et 51 s. Dans le modèle théorique, on considère que la puissance totale Ptot développée par le cycliste, lors de la montée, va permettre de : - vaincre les forces de pesanteur pour permettre l’ascension (Pasc) ; - lutter contre les frottements mécaniques des roues sur le bitume (Proulement) ; - contrer les frottements de l’air (Pair). Dans ce modèle, les puissances Pasc et Proulement sont proportionnelles à la vitesse du cycliste alors que Pair est proportionnelle au cube de cette vitesse. 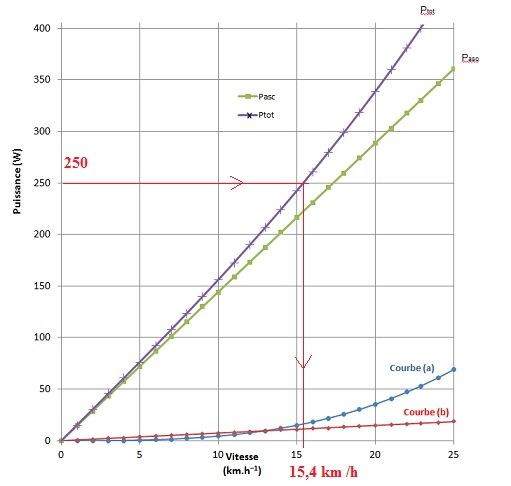Le modèle théorique utilisé permet de construire le graphique suivant qui donne les valeurs des différentes puissances en fonction de la valeur de la vitesse lors de l’ascension du col. 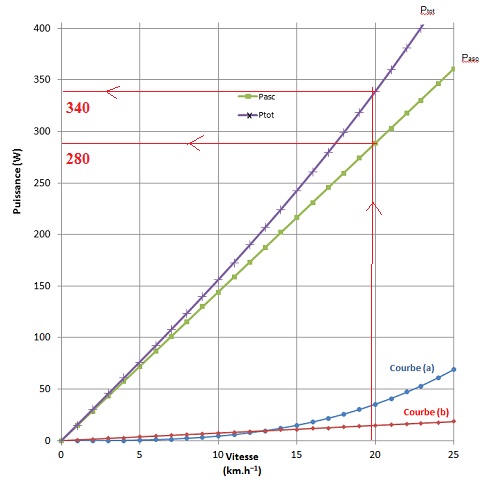Données :  Intensité de la pesanteur g = 9,8 m.s–2.  Pour une puissance constante sur la durée considérée, la variation d’énergie E s’exprime par : E = P. t , avec E en joule, t en seconde et P en watt. On étudie le système S {cycliste, équipement, vélo} de masse m= 67,8 kg. On suppose que l’ascension se fait à vitesse v constante et à puissance Ptot constante. 1. Questions préliminaires 1.1. Dans quel référentiel sont effectuées les mesures ? Les mesures sont effectuées dans le référentiel terrestre supposé galiléen. 1.2. Montrer que la vitesse moyenne du cycliste, lors de l’ascension, vaut v = 19,6 km.h–1. 31 min 51 s = 31 x60 +51 = 1911 s ; v = distance / durée = 10,4 103 / 1911 =5,44 m /s ou 5,44 x3,6 = 19,6 km /h. 1.3. Définir l’énergie mécanique Em d’un système. Que peut-on dire alors de l’évolution de cette énergie lors de l’ascension ? L'énergie mécanique est la somme de l'énergie cinétique et de l'énergie potentielle. L'énergie cinétique reste constante. L'énergie potenteillle -( origine au pied du col) augmente. l'énergie mécanique croît lors de l'ascension. 2. Étude de l’ascension du col par le cycliste et validation du modèle de calcul de puissances. On cherche à valider le modèle proposé en utilisant les données du capteur SRM lors de l’ascension du col par le cycliste. 2.1. Donner l’expression littérale de la variation d’énergie potentielle de pesanteur Epp du système entre le pied et le sommet du col de la Hourquette d’Ancizan, en fonction de m, g et de ZA et ZB, (respectivement altitudes du pied (759 m) et du sommet du co ( 1564 m)l). Montrer que Epp = 5,3 × 105 J. Epp = mg(zB-zA) = 67,8 x9,8 (1564-759)= 5,3 × 105 J. .... ..... 2.2. À partir du résultat de la question 2.1, calculer la valeur de Pasc et vérifier sur le graphique 1 qu’elle correspond bien à celle du modèle proposé. Pasc = Epp / Dt = 5,3 105 / 1911 =277 ~2,8 103 W. 2.3. Parmi les courbes (a) et (b) du graphique 1, identifier, en explicitant votre raisonnement, celle qui représente Proulement et celle qui représente Pair . En déduire les valeurs de Proulement et Pair, lors de l’ascension du col par le cycliste. Courbe a : Proulement est proportionnelle à la vitesse ( droite passant par l'origine). Courbe b : Pair est proportionnelle au cube de la vitesse. 2,4 cm correspondent à 100 W. Proulement : 0,4 cm correspond à : 0,4 x100 / 2,4 ~17 W. Pair : 0,9 cm correspond à : 0,9 x100 / 2,4 ~37 W. 2.4. En utilisant le graphique 1, déterminer la puissance totale Ptot prédite par le modèle lors de l’ascension. Les mesures réalisées par le capteur SRM, placé sur le pédalier du cycliste, permettent-elles de valider le modèle ? Ptot ~340 W d'après le graphe. D’après http://www.srm.de/news/road-cycling/le-tour-de-france-stage-9/ 400 W correspond à 6,6 cm. Ptot SRM = 400 x5,2 / 6,6 ~ 320 W. Le modèle est valide. 3. Prédiction de performances à partir du modèle Un cycliste amateur développe une puissance totale constante Ptot = 250 W lors de la montée. En utilisant le modèle étudié, donner une estimation de la durée de l’ascension du col par le cycliste. Durée = distance  / vitesse = 10,4 / 15,4 =0,675 heure ou 40 min 31 s. Partie 2 : Étude de la physiologie de l’effort et régulation du pH sanguin Lors des efforts physiques, des mécanismes biologiques ont pour conséquence la production d’acide lactique par l’organisme. Cet acide a été identifié comme responsable, puis témoin de la fatigue et il est aujourd’hui un indicateur de plus en plus utilisé pour évaluer l’impact d’un entrainement. En effet, pendant un exercice, la concentration en ions lactate dans le sang augmente. Dès 1930, Owles définit un niveau métabolique critique, appelé « seuil lactique », par l’intensité d’exercice au-dessus de laquelle le taux de lactate dans le sang s’accroît rapidement alors que le taux de bicarbonate plasmique baisse. D’après http://www.volodalen.com Dans cette partie, on étudie les mécanismes de régulation qui interviennent lors de l’acidification del’organisme au cours de la pratique d’un sport d’endurance comme le cyclisme. Données : Valeurs normales dans le sang, à 37 °C et en l’absence d’efforts : pH sanguin = 7,4 (limites compatibles avec la vie : 7,0 à 7,8 unités de pH) ;  le pH intramusculaire varie entre 7,1 et 6,1 ;  concentration en ions hydrogénocarbonate (aussi appelés ions bicarbonate) : [HCO3-]0 = 25 mmol /L. le CO2 dissous dans le sang est sous la forme H2CO3 (aq) ; concentration en CO2 dissous dans le sang : [H2CO3]0 = 0,9 mmol.L–1. 1. L’acide lactique. L’acide lactique, dont la formule est donnée ci-dessous, est formé dans l’organisme à partir de l’acidepyruvique selon une réaction d’oxydoréduction catalysée par la LDH (lactate  déshydrogénase). 1.1. Déterminer les groupes caractéristiques présents dans l’acide lactique et associer à chacun d’eux la famille chimique correspondante. 1.2. En utilisant la représentation de CRAM, donner les différents stéréoisomères de configuration de l’acide lactique en précisant la relation de stéréoisomérie qui existe entre eux. Fonction alcool secondaire et fonction acide carboxylique. 2. Influence de la production d’acide lactique sur le pH sanguin Le « seuil lactique », facteur déterminant de la performance en course longue telle que la course cycliste, est utilisé dans le suivi des cyclistes. Il correspond à la concentration en ions lactate à ne pas dépasser pour optimiser les performances et limiter la fatigue. On fixera la valeur de ce « seuil lactique » à 3,0 mmol.L–1. On s’intéresse à la formation d’acide lactique par l’organisme, en l’absence de régulation de pH. 2.1. L’ion lactate est la base conjuguée de l’acide lactique. Représenter la formule semi-développée de l’ion lactate en faisant apparaître les doublets libres. Pour la suite de l’exercice on notera AH l’acide lactique et A- l’ion lactate. 2.2. Écrire l’équation de la réaction chimique entre l’acide lactique et l’eau (réaction 1). CH3-CHOH-COOH (aq) + H2O(l) = CH3-CHOH-COO- (aq) +H3O+aq. 2.3. Comparer les quantités de matière en ions oxonium H3O+aq (aq) et en ions lactate produites lors de la réaction 1. La solution étant électriquement neutre, les quantités de matière en ions oxonium H3O+aq (aq) et en ions lactate produites lors de la réaction 1. 2.4. En déduire quel serait le pH du sang quand le « seuil lactique » est atteint, lors d’un effort, en absence de régulation. En déduire si une régulation du pH sanguin est nécessaire. [CH3-CHOH-COO- (aq)]=[H3O+aq]= 3 10-3 mol/L; pH = -log(3 10-3) ~2,5 en absence de régulation. Cette valeur est en dehors des limites compatibles avec la vie : 7,0 à 7,8 unités de pH) ; une régulation est donc indispensable. 3. Régulation du pH sanguin. On s’intéresse à la régulation par le système « tampon bicarbonate » faisant intervenir le couple H2CO3(aq) / HCO3- aq . On raisonnera en l’absence de toute autre réaction acido-basique. 3.1. Écrire l’équation de la réaction entre l’acide lactique et les ions hydrogénocarbonate, réaction considérée comme totale (réaction 2). CH3-CHOH-COOH (aq) +  HCO3- aq = CH3-CHOH-COO- (aq) +H2CO3(aq) Expliquer alors la phrase : « le taux de lactate dans le sang s’accroît alors que le taux de bicarbonate plasmique baisse ». Dans le sens direct, la réeaction (2) consomme des ions bicarbonate et produit des ions lactate. 3.2. Montrer que lorsqu’on atteint le « seuil lactique », et si seule la réaction (2) contribue à former du H2CO3, la valeur de la concentration de H2CO3 à l’état final a augmenté par rapport à sa valeur normale et vaut [H2CO3]f = 3,9 mmol.L–1. Avancement volumique ( mmol/L) CH3-CHOH-COOH (aq) +  HCO3- aq = CH3-CHOH-COO- (aq) +H2CO3(aq) initial 0 0 25 0 0,9 final 3 3 25-3 3 0,9 +3 3.3. Si on ne considère que cette réaction (2), le pH du sang peut être calculé grâce à l’équation de Henderson-Hasselbalch : pH = 6,1 + log ([HCO3 - ]f / [H2CO3]f) Montrer que [HCO3- f / [H2CO3]f= 5,6 à l’atteinte du seuil lactique. Cette régulation du pH sanguin est-elle efficace ? [HCO3- ]f / [H2CO3]f= 22 /3,9 =5,6. pH = 6,1 +log(5,6) ~6,9. Cette régulation de pH est efficace puisque l'on passe de pH=2,5 à 6,9. 3.4. Expliquer pourquoi d’autres systèmes tampons jouent forcément un rôle dans la régulation du pH de l’organisme. Cette valeur 6,9 est en dehors des limites compatibles avec la vie : (7,0 à 7,8 unités de pH) ; une autre régulation est donc indispensable 3.5. Les poumons interviennent en second lieu, après la régulation par les systèmes tampons. Expliquer quel peut être leur rôle. En éliminant le gaz carbonique produit par l'organisme, les poumons éliminent H2CO3(aq) .

menu